It was night outside long before the business was over, and nothing was to be seen but the dim eyes and the claws.
Herbert Wells. The Invisible Man. 1897.
Herbert Wells went three times in Russia. During his second visit — then there was already the Soviet Union – he met Yakov Isidorovich Perelman, who submitted to the attention of the author of “The Invisible Man” the following fact: if a man is completely invisible, then the crystalline lens of his eyes are invisible, and therefore they do not refract the light and do not convey the images on the retina. For this man everything is invisible!
But are there invisible bodies, albeit inanimate? In 2009, mathematicians have shown that there exists inanimate invisible beings!
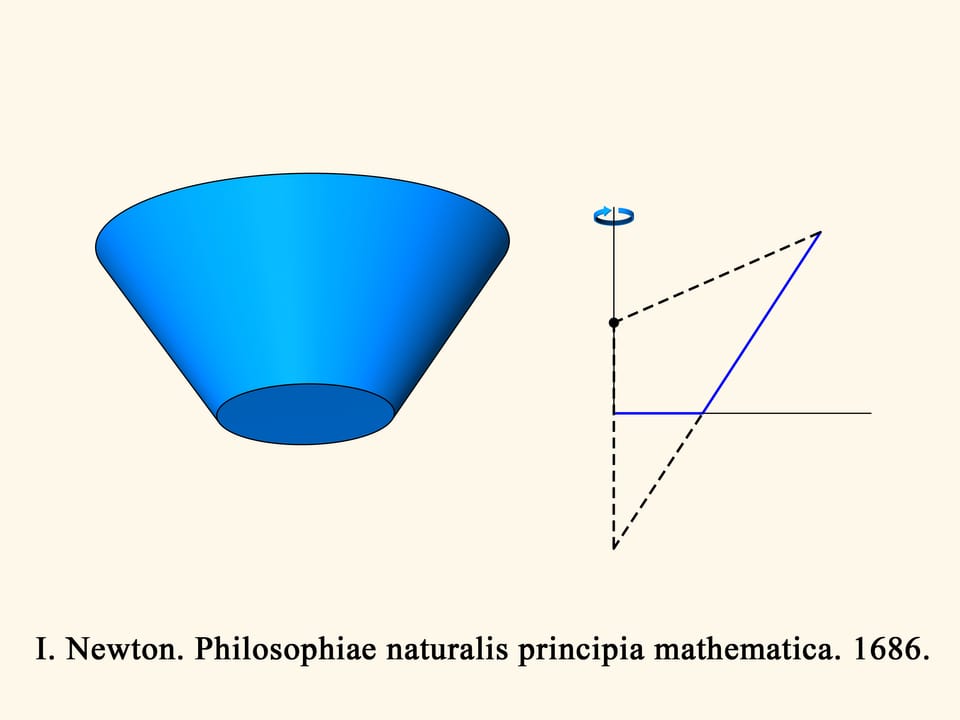
Let us start from the seventeenth century. In “Mathematical Principles of Natural Philosophy” (“Philosophiae Naturalis Principia Mathematica”) Isaac Newton studied the problem of the fall (or movement) of different bodies in a “rarefied medium, consisting of identical particles, arbitrarily placed at equal distances from one another” that bounce elastically when they collide with the bodies. Later this problem was called “Newton’s aerodynamic problem.”
The first two bodies considered are a sphere and a cylinder, both with the same diameter. Which of these bodies meet less resistance? Newton shows by geometric methods that the resistance for the sphere will be twice lower.
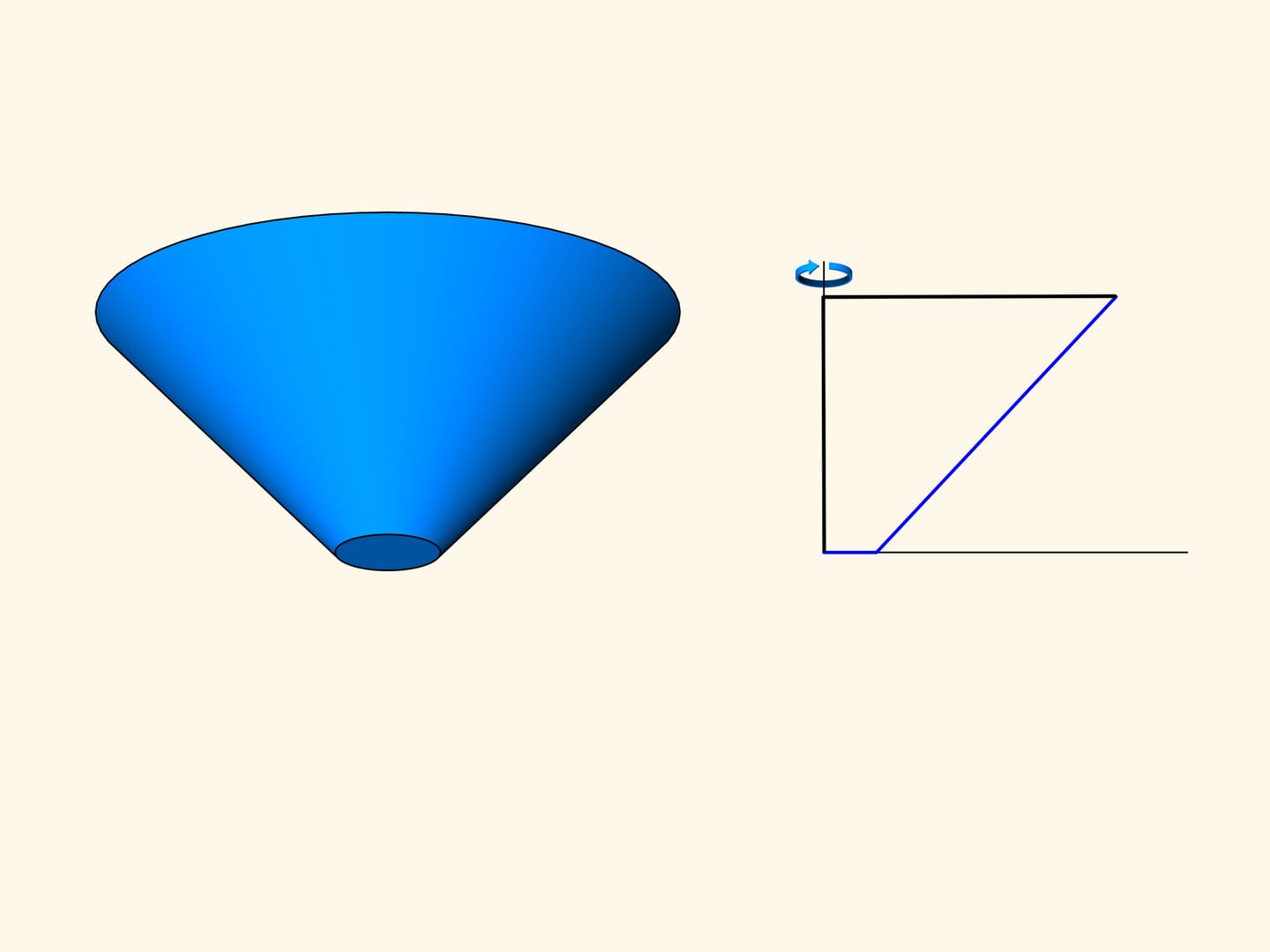
In a second time Newton begins to study the truncated cones: among all the truncated cones with the radius of the bigger base and the height fixed, find the one for which the resistance in a rarefied medium — for a motion along the axis of the cone — is minimal.
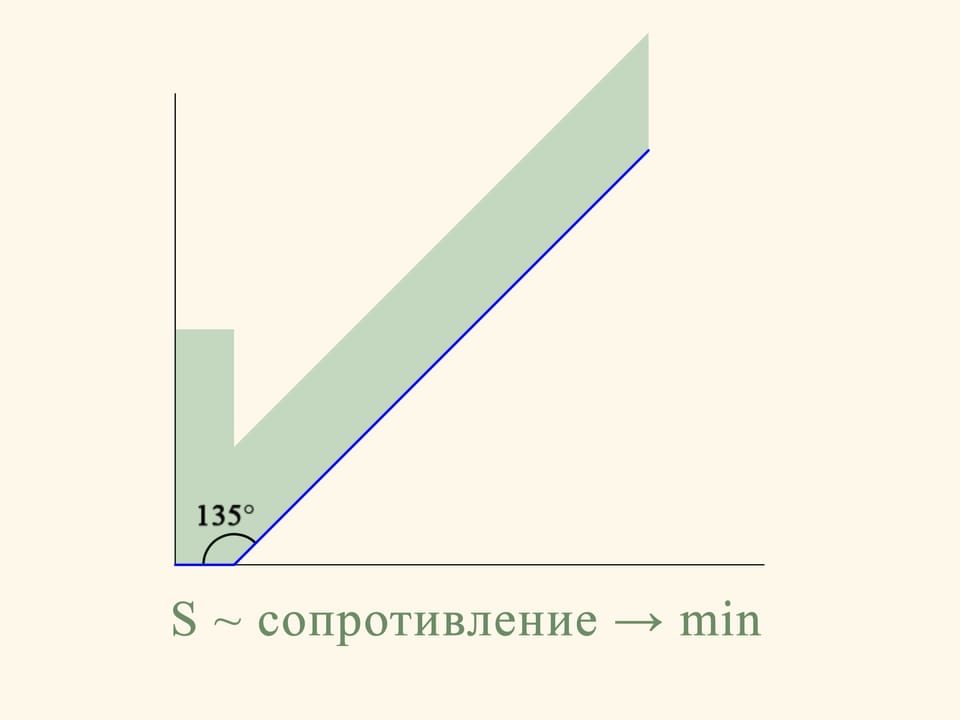
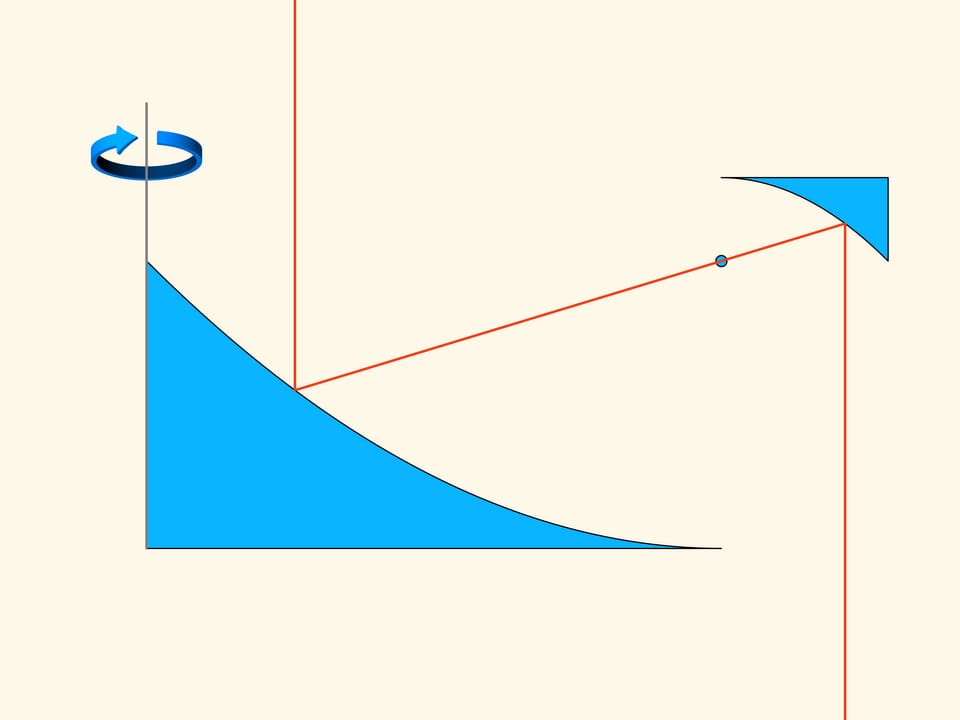
Let us consider a section of the truncated cone and the problem in the planar case.
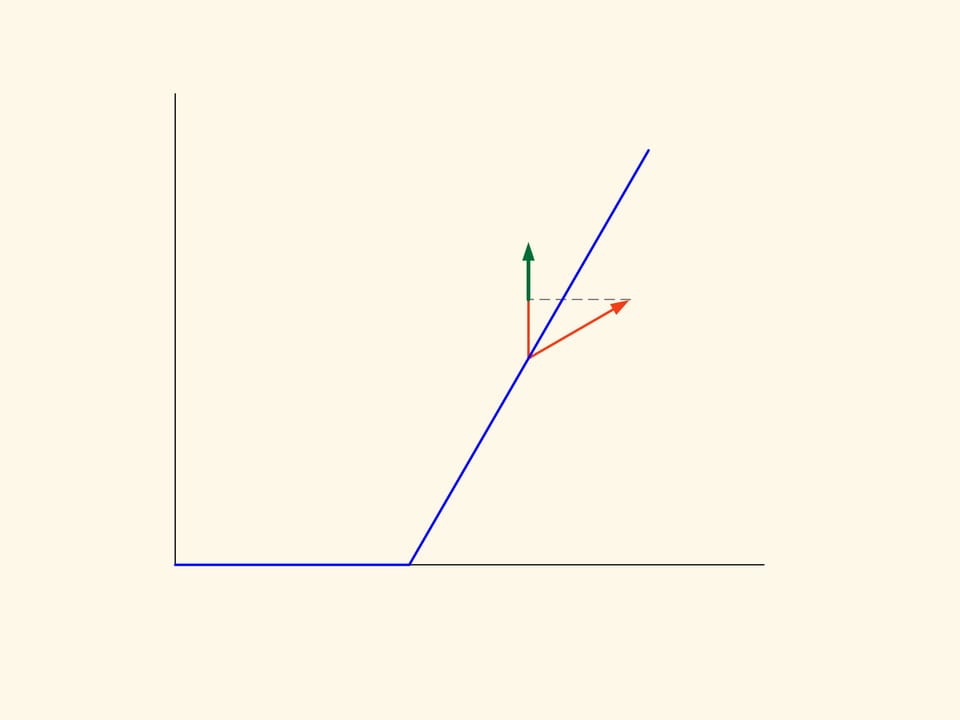
What is the resistance? While the cone falls, it collides with the spheres — the particles of the rarefied medium. One part of the spheres collide with the lower surface of the truncated cone, and a part with the lateral surface, some of them move without stopping and without suffering the effect of the body. When it collides with the truncated cone a particle changes its direction of motion according to the law that “the angle of incidence equals the angle of reflection”. The resistance that the sphere has put up to the fall of the truncated cone consists in the change of the vertical component of the momentum vector of the sphere. Since the sphere evenly on average hit the surface of the body, the thrusts to the left and to the right cancel out and should be not considered.
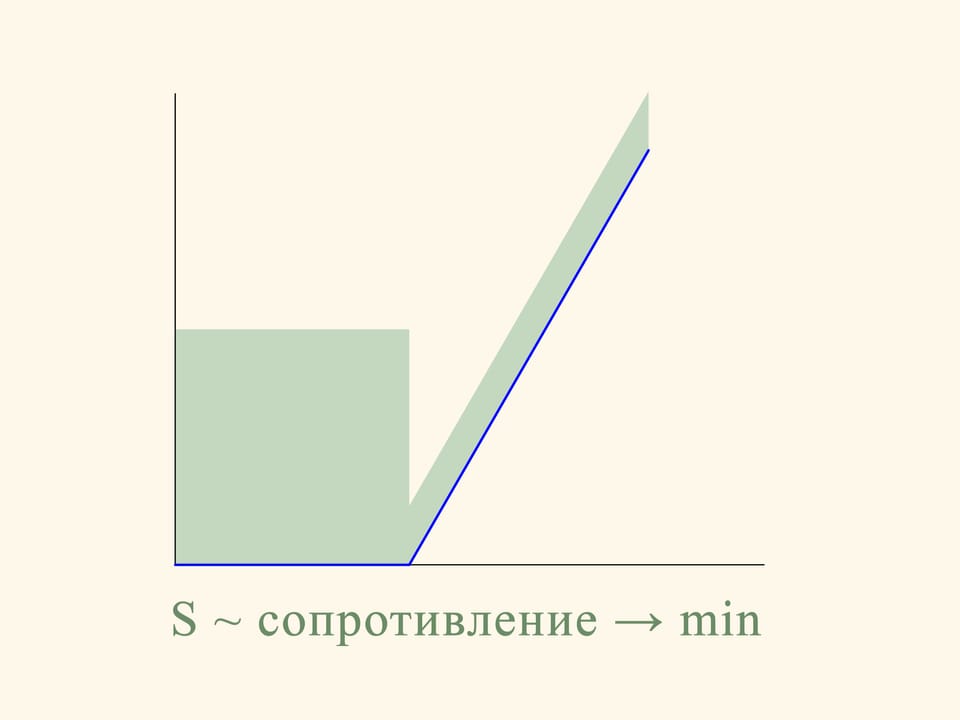
In the planar case the resistance of the section of the truncated cone is proportional to the sum of the area of a rectangle constructed on the smaller base of the trapezium and the area of a parallelogram, constructed on the oblique side. And this resistance must be minimized. If we do the calculation, we find that the area of the figure in green is minimal when the angle between the base and the oblique side is equal to 135°. That is, the sphere after the collision with the oblique side moves in a strictly horizontal direction.
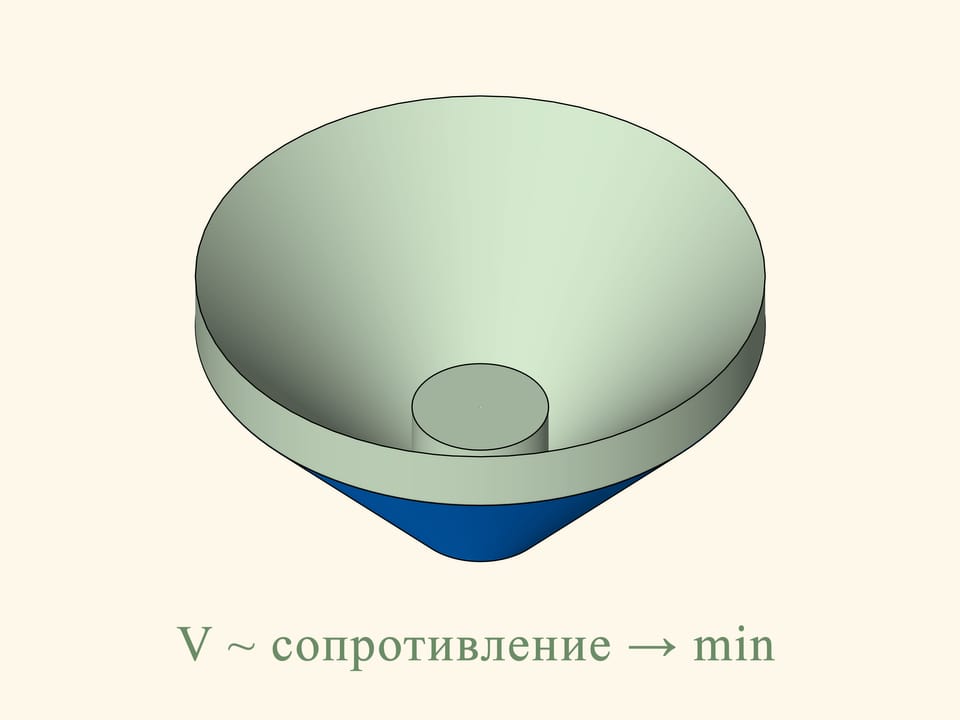
From the planar solution of the problem, can we deduce that the section of the optimal truncated cone will satisfy the same condition for the three-dimensional problem? It turns out that this is not true. To move from one section of an object to the object itself, we must rotate the planar section around the vertical axis. The small pieces of the surface farthest from the axis, contributing to the area, describe during the rotation a trajectory much longer and will therefore make a greater contribution to the volume. By consequence, we cannot find the minimum volume in the three-dimensional problem using the minimum of the area in the plane.
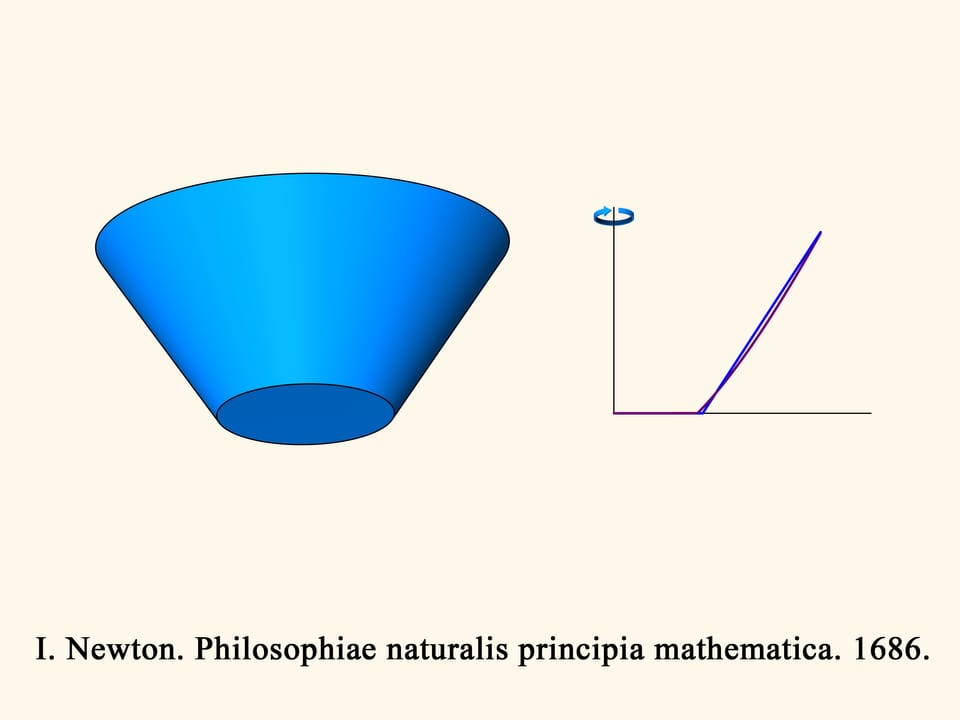
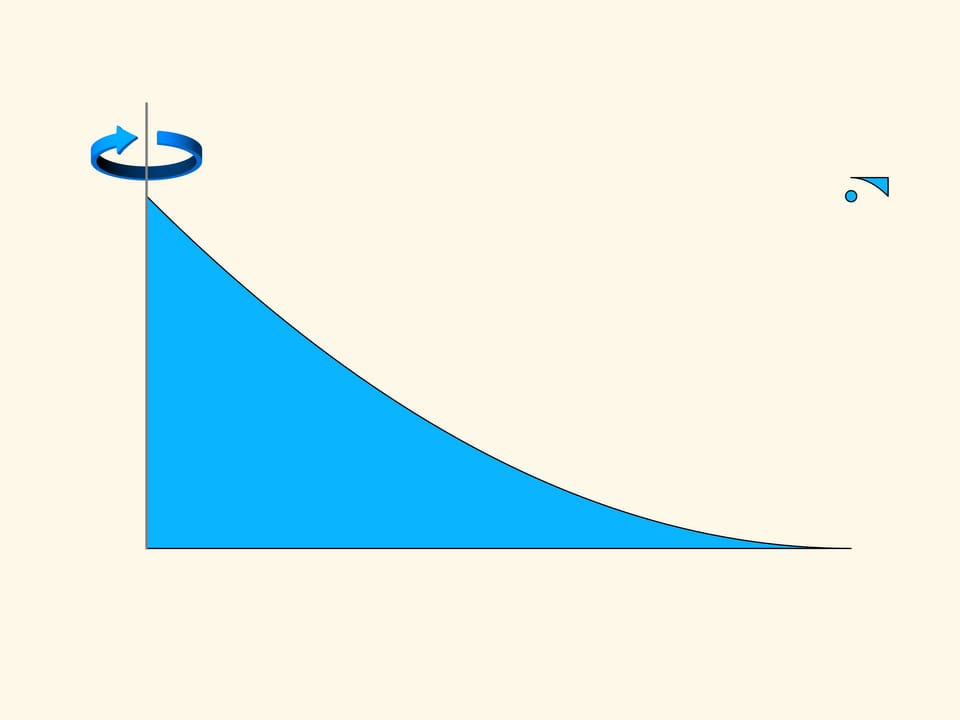
In the three-dimensional case the resistance of the blue cone is proportional to the volume of the green solid, and we have to find the minimum of this volume, among all truncated cones. Newton shows that the truncated cone will be optimal – i.e., it meets the least resistance — under the following condition. Take the midpoint of the height of the trapezium and connect it with the extreme point of the base by a straight segment. Add a vertical segment of this length below the midpoint considered. The optimal cone is obtained by rotating the base of the isosceles triangle thus obtained. It is surprising that the solid that meets the least resistance is not a cone but a truncated cone!
But what will be the best convex solid of revolution, best in the sense of least resistance, with a given width and a given height? Although at that time the variational calculus did not exist yet (these problems are now solved by this method), Newton finds the answer to this question. He shows that the best convex solid of revolution does not differ much from the optimal cone, and calculates the exact generating curve of this solid.
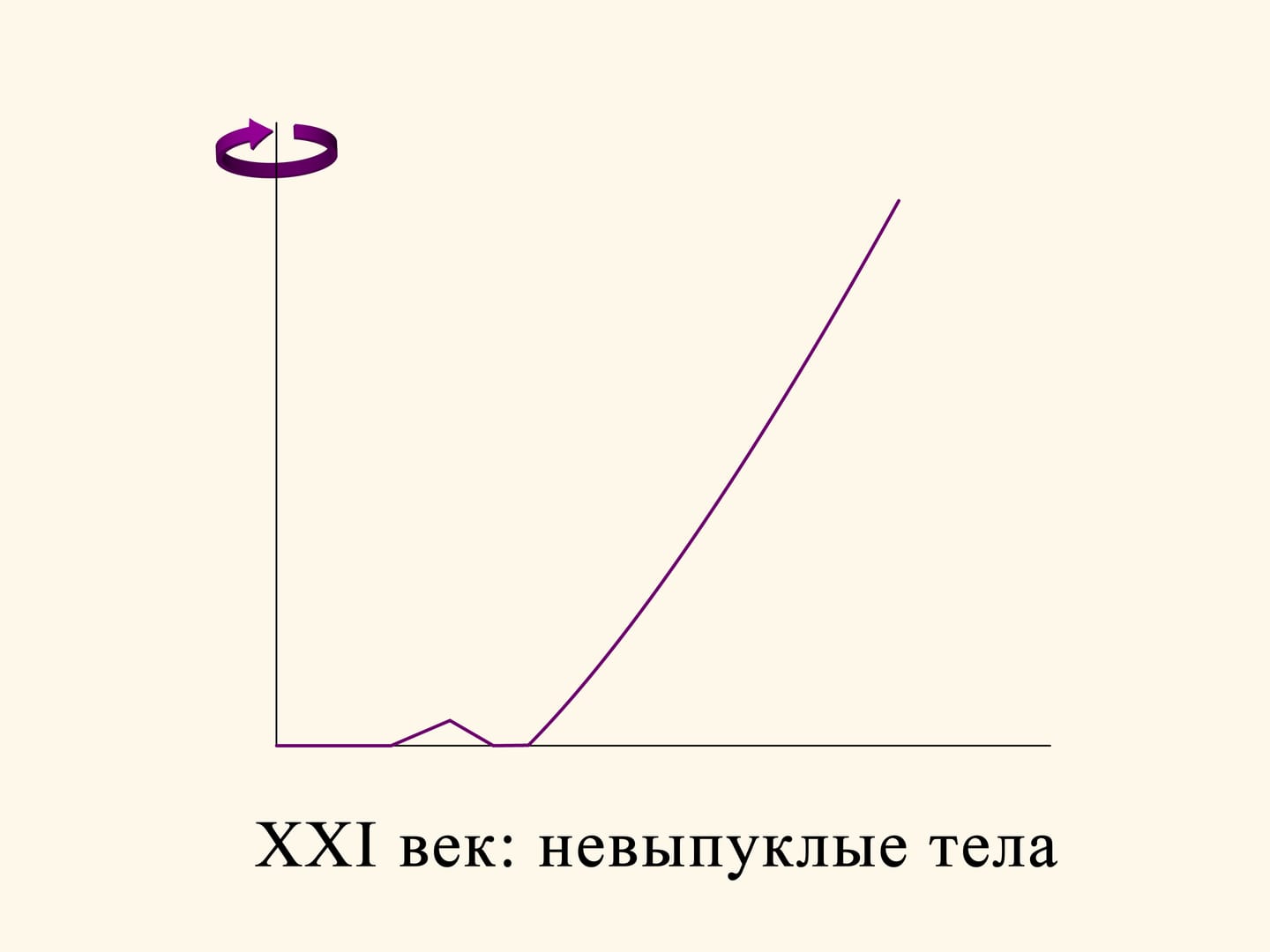
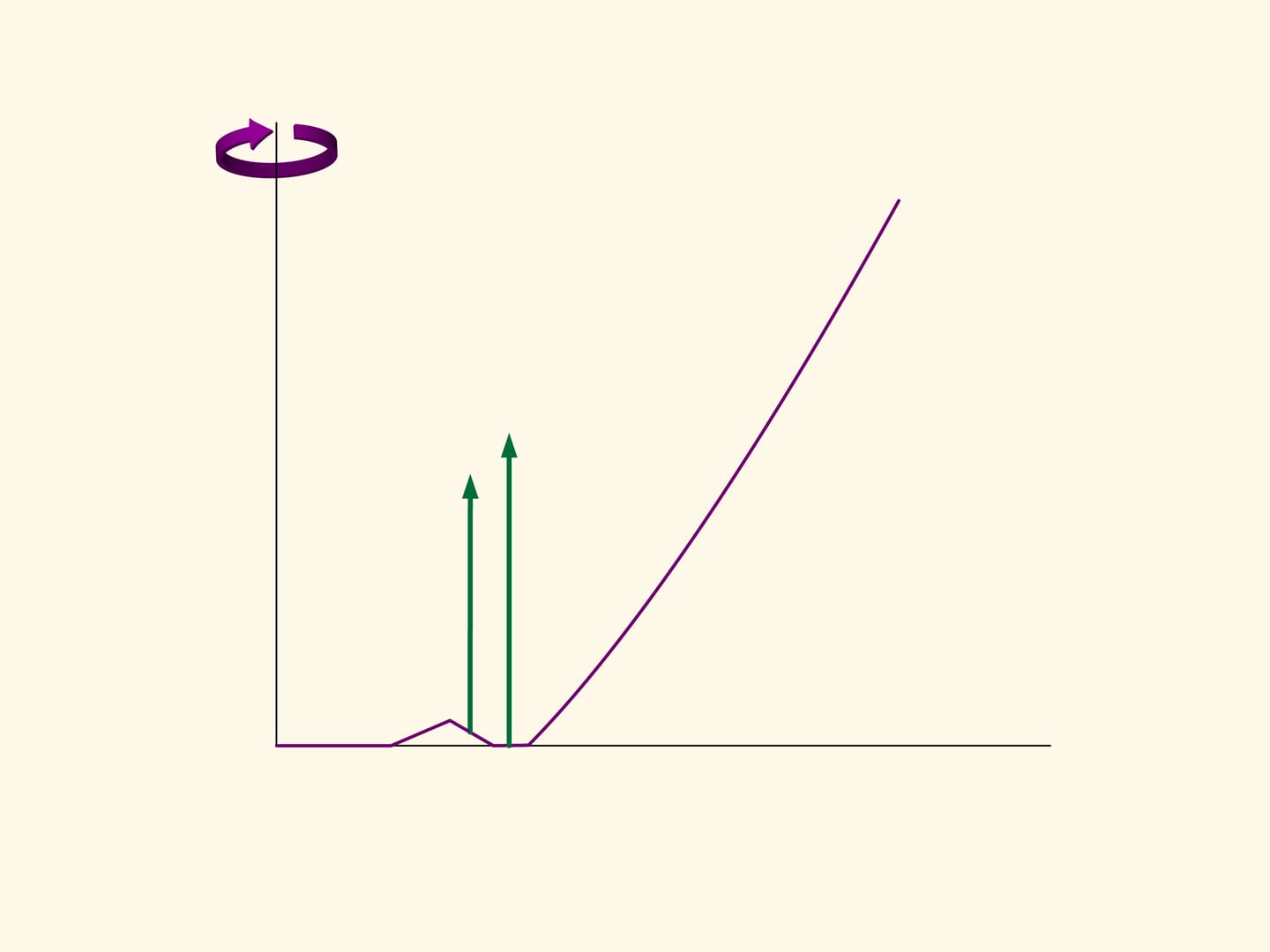
Since the time of Isaac Newton, for more than 300 years, scientists considered the aerodynamic problem in a rarefied medium in its initial formulation: find a convex solid of revolution. It seemed natural that the best solid should be convex. Only in the twenty-first century mathematicians tried to waive the condition of convexity, and this led to an amazing achievement!
Take, for instance, the section of the optimal solid found by Newton, and make a triangular hole in its flat part. The solid of rotation obtained is already no more convex, but its resistance decreased with respect to that of the convex solid. In fact, if the groove is not too deep, then a sphere, after a collision, bounces in oblique and does not collide with the solid any more. The vertical component of the momentum vector of the sphere, and, consequently, the braking impressed by the impact will be lower than for a rebound on a horizontal surface.
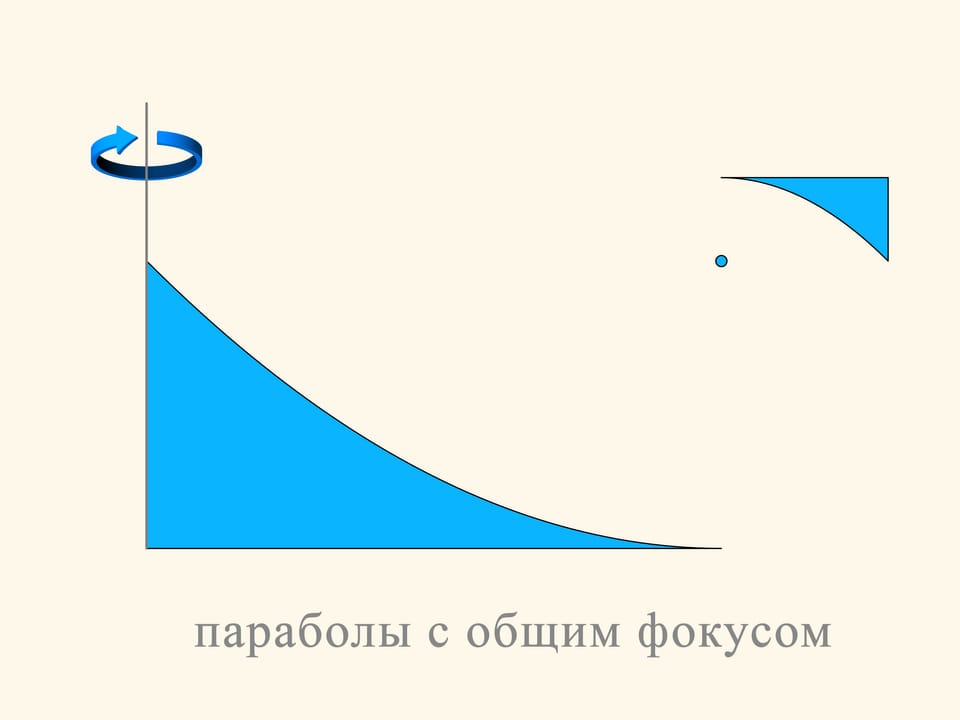
We will observe two interesting constructions of non-convex solids, exposed in the work of A. Yu. Plakhov.
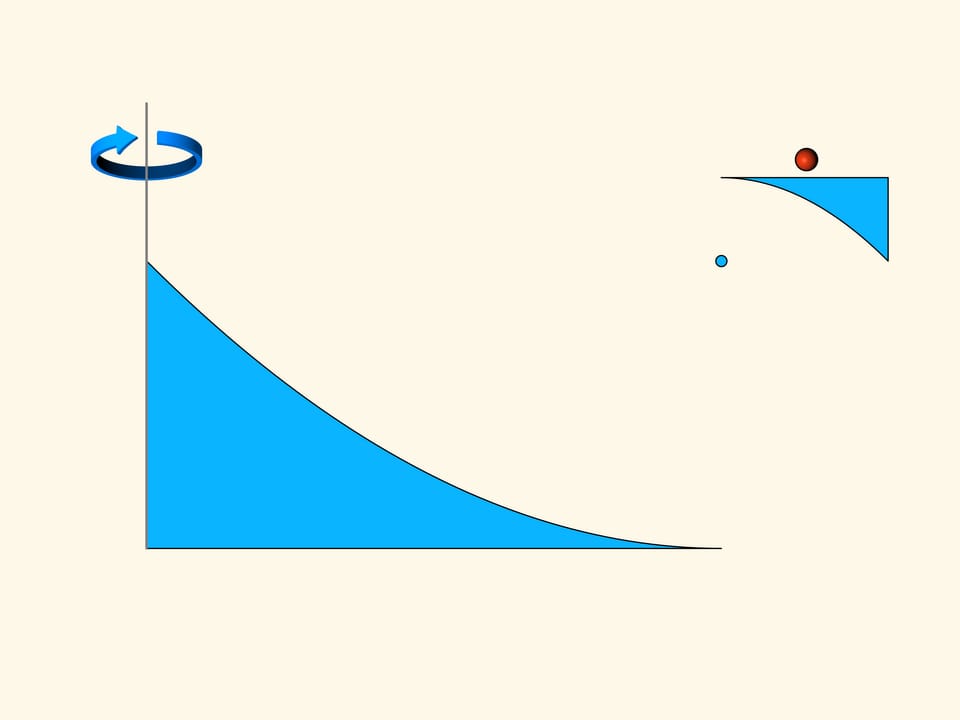
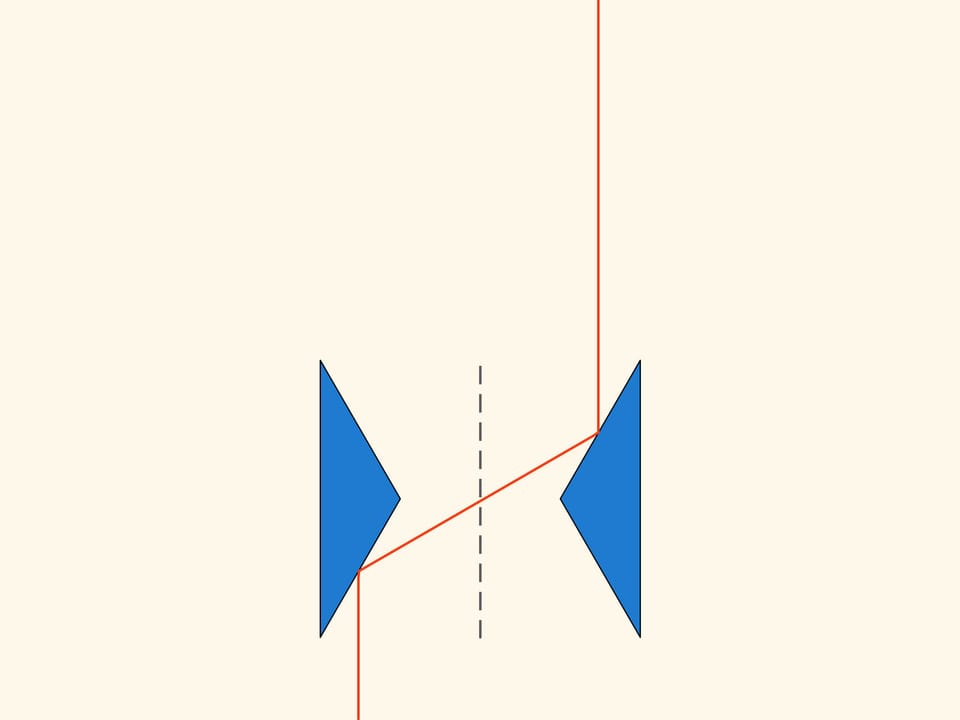
The plane section of the first construction consists of two pieces of parabolas, arranged so that their focuses and their axes coincide. The motion will be in the direction of the axis of parabolas. As you remember, the parabola has the optical property that the rays parallel to its axis, after reflection on the parabola, pass through its focus. In the construction we consider, part of the spheres that collide with it, fall into the horizontal segment tangent to the top of the small parabola and put up resistance to the motion. But most of the spheres are reflected by the big parabola, pass through the focus, and then are reflected by the small parabola and go away in a direction parallel to the initial one. In the Newton rarefied medium these spheres do not increase the resistance because they do not lose the vertical component of their momentum, and after the collisions they exit in a direction parallel to that with which they entered, only displaced in horizontal.
The part of the construction that reflects the spheres can be made small, without changing the basic concept of the same construction.
Let us rotate the construction of the two parabolas about the vertical axis. We obtain a solid that recall a flying saucer. If we look at it from above, we see that the surface of this disk is very large. The surface on which the resistance is generated can be made as small as we wish. For a motion in the direction of its axis this solid of revolution in a rarefied Newton medium will meet a resistance as little as we want.
But do they exist bodies with no resistance at all? It happens that also such bodies exist!
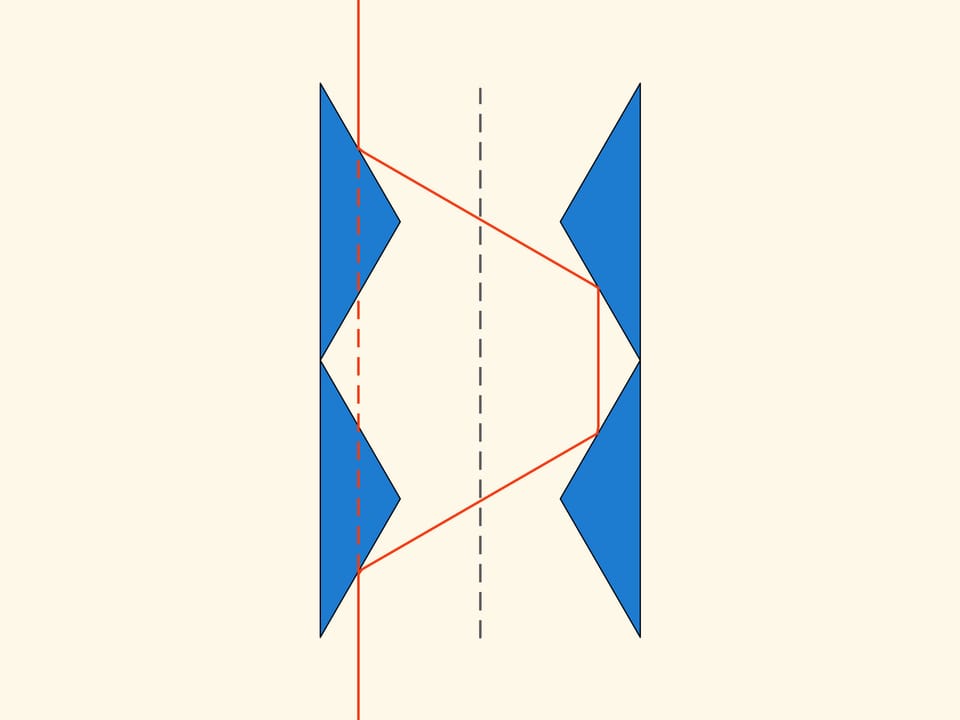
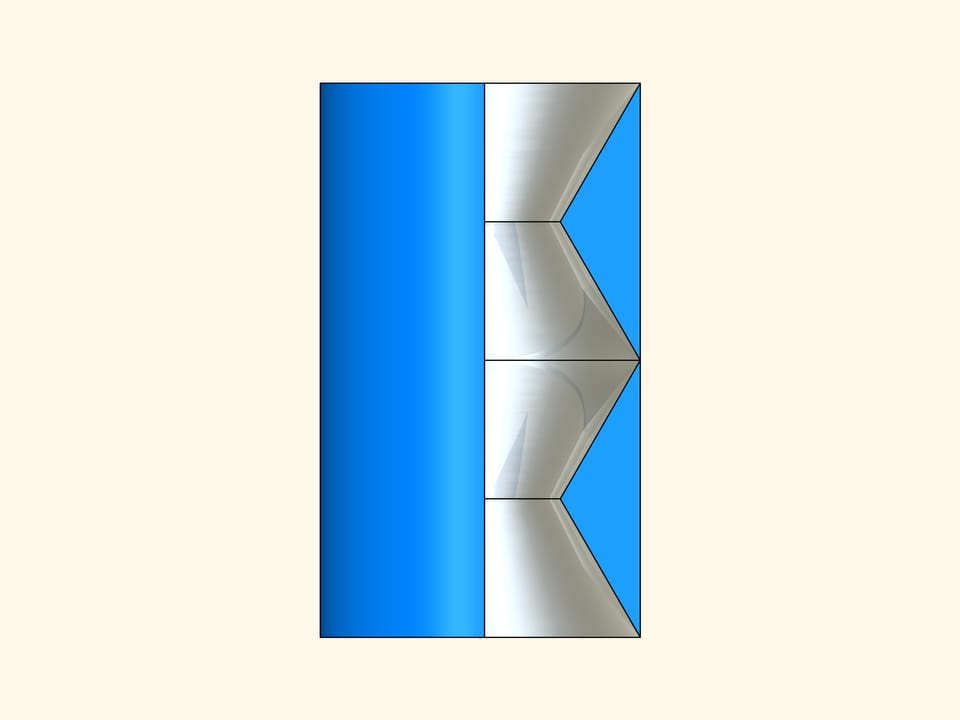
The construction is based on a triangle with angles of 30, 30 and 120 degrees. Take another triangle symmetrical with respect to the vertical axis at a distance of two heights.
We look at what happens when this planar construction moves in the direction of the axis of symmetry in a rarefied Newton medium. With some spheres it will not collide at all, so that such spheres have no influence on the motion. But those spheres, with which it collides, are always reflected on both the triangles and exit in a direction parallel to the axis of symmetry, without changing their momentum vector. In this way, the resistance of the solid obtained by rotating this construction about its axis of symmetry, is equal to zero!
To follow the trajectory of the spheres — the particles of the medium — we have represented their trajectories in the form of rays. But it is exactly along these trajectories that a ray of light propagates! If the last construction of the two triangles is made of reflecting surfaces, then the right and left parts of the images that we see through it, are exchanged. But if we take a second identical construction and put it over the first, then the optical system so obtained will neither deflect the rays, nor reverse them.
Now we rotate the planar construction around its axis of symmetry and we ensure that all internal surfaces are mirror. We get a solid that from outside is a cylinder whereas inside is made of four conical reflecting surfaces. If we look through this cylinder along its axis of symmetry, then it will be invisible!
In his work, A.Yu.Plakhov also consider how to make an invisible envelop to any body. An object covered with a similar mantle becomes almost invisible!
Obviously, these constructions do not deviate (or almost do not deviate in the case of the invisible mantle) only those rays that are parallel to the axis of symmetry. And for the human eye the “invisible cylinder” will be in fact almost invisible, only if seen from far enough. It is possible that some of you, using the knowledge of mathematics, and, perhaps, of other sciences, in the future be able to build objects completely invisible.