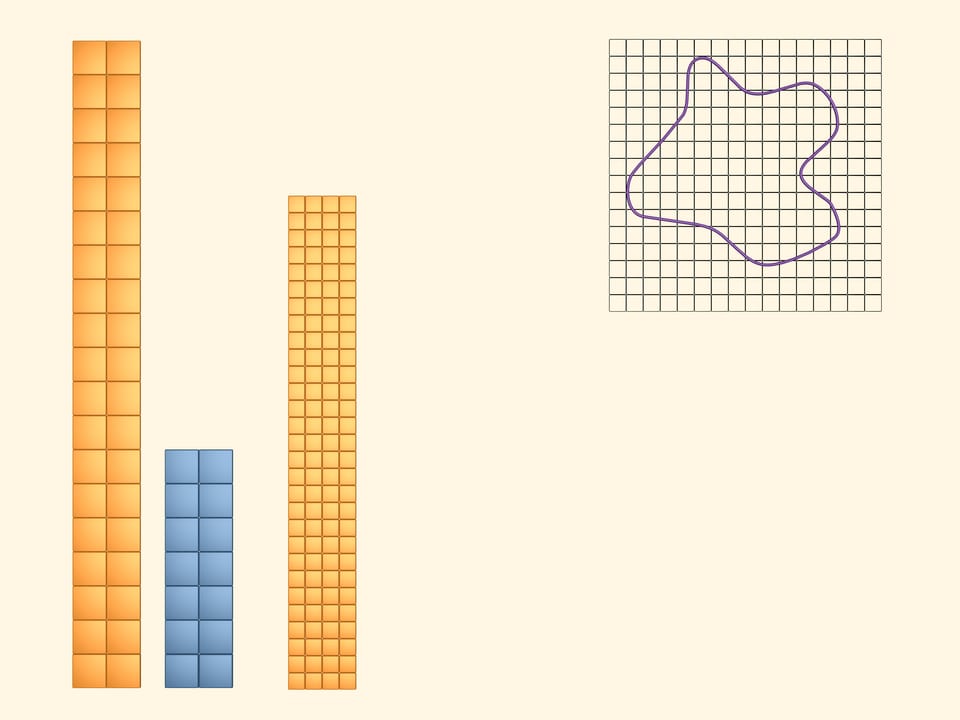
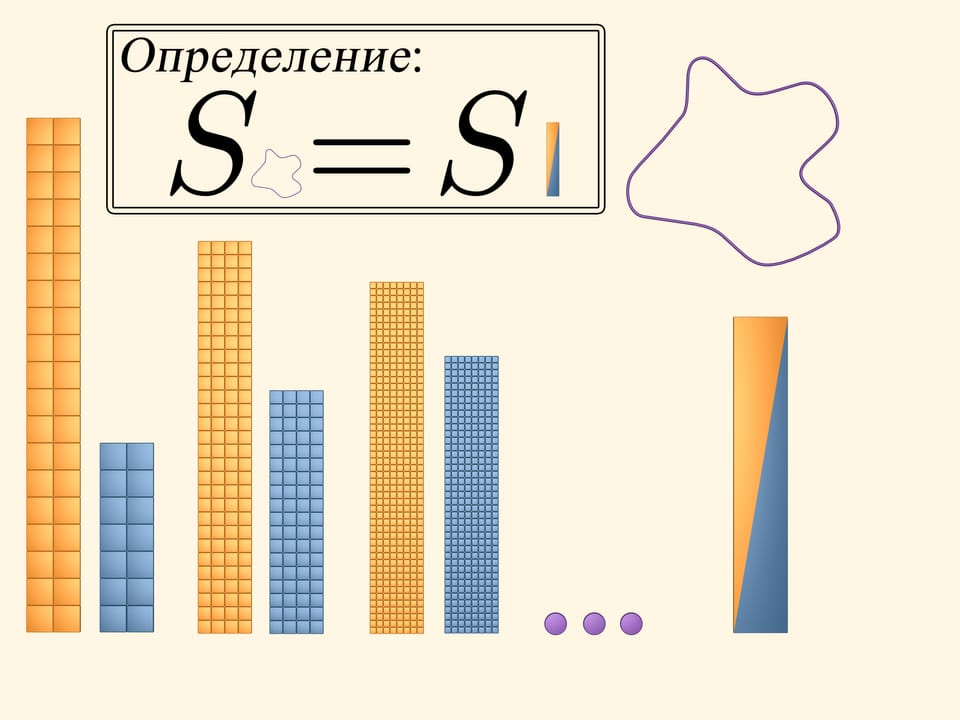
L’aire du carré est égale au carré de la longueur de son côté. Il est facile de calculer l’aire d’une figure qui peut être divisée en plusieurs carrés. Mais quelle est l’aire d’une figure délimitée par une courbe quelconque?
Nous allons superposer sur la figure plane en question un réseau carré.
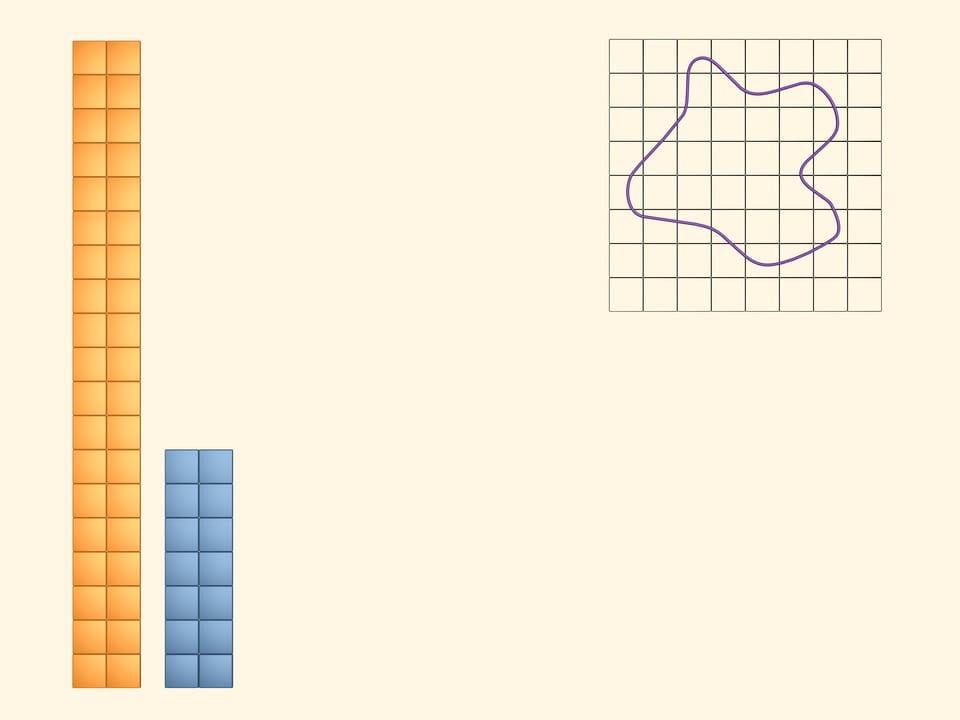
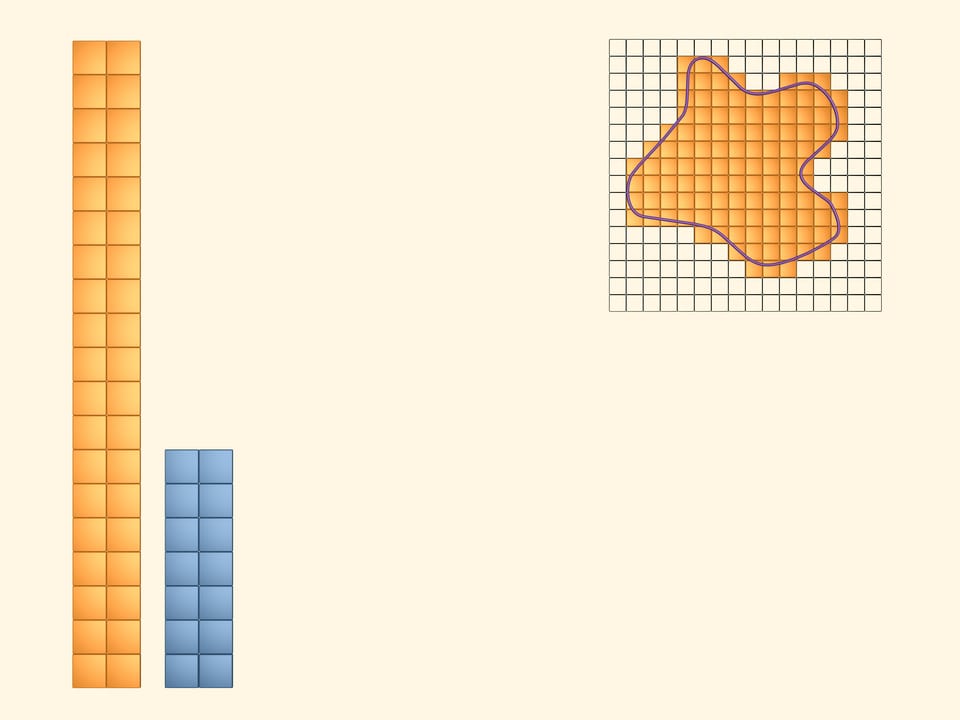
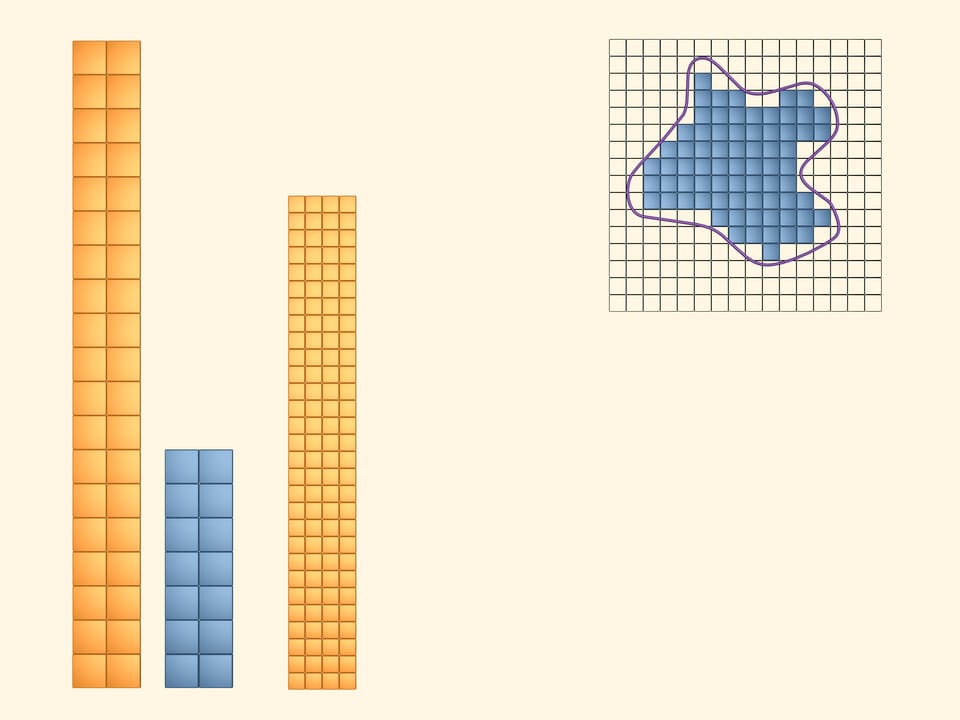
Colorions en jaune toutes les cases qui son couvertes par la figure au moins partiellement. Pour visualiser et calculer l’aire de la surface occupée par les carrés jaunes, nous construisons un rectangle avec eux. Il est évident que la quantité, que nous appelons aire de la figure en question, est plus petite de l’aire de ce rectangle jaune.
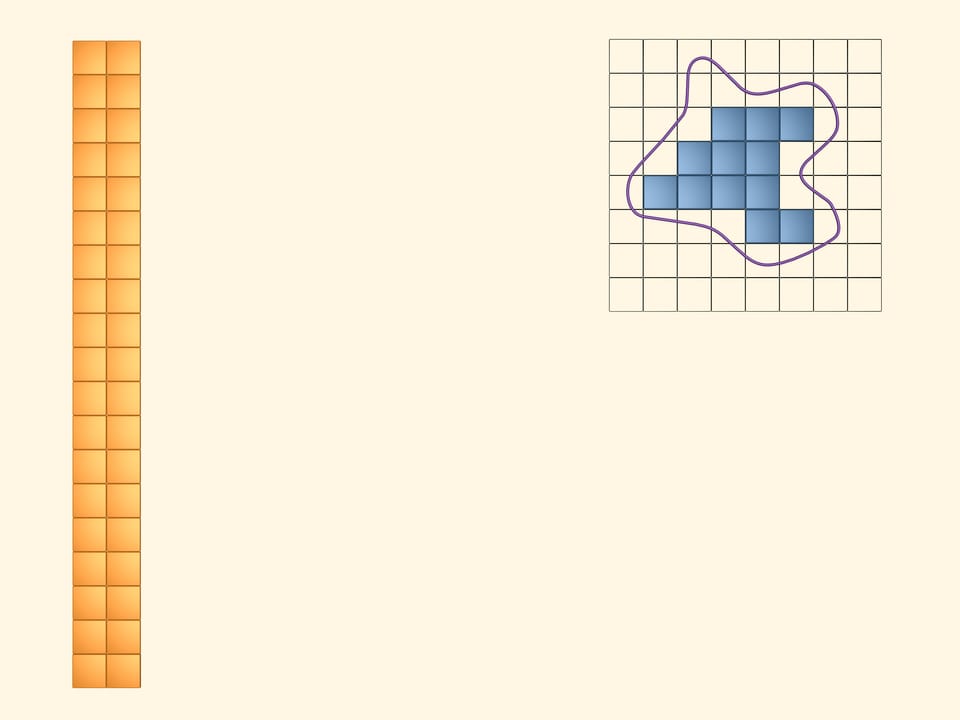
Colorions maintenant en bleu tous les carrés qui se trouvent complètement à l’intérieur de notre figure. De ces carrés il y en a moins, bien sûr, que des jaunes. Aussi avec ces carrés nous allons construire un rectangle. L’aire de notre figure est plus grande que l’aire de ce rectangle bleu.
Donc ce que nous appellerions l’aire de la figure en question est plus grand que l’aire du rectangle bleu et est plus petit que l’aire du rectangle jaune. Mais les aires de ces deux rectangles sont assez différentes, et jusqu’à présent nous n’avons pas l’aire de notre figure.
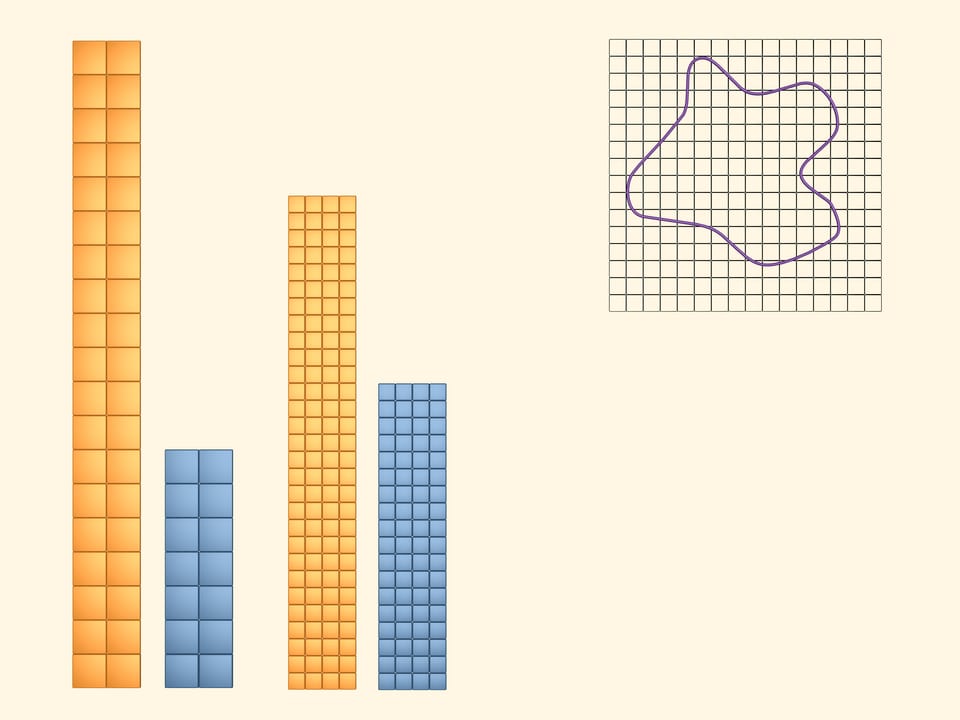
Pour obtenir des limites inférieure et supérieure plus précis pour la quantité cherchée, considérons un réseau carré avec des cases plus petites. Nous répétons les étapes ci–dessus. Colorions en jaune les carrés qui sont couverts par la figure au moins partiellement. Et colorions en bleu ceux qui sont entièrement à l’intérieur de la figure. Encore une fois l’aire de la figure est plus grande que celle du rectangle bleu et plus petite que celle du rectangle jaune. Mais cette fois, après avoir pris un réseau plus fin, nous obtenons que les limites supérieure et inférieure se rapprochent.
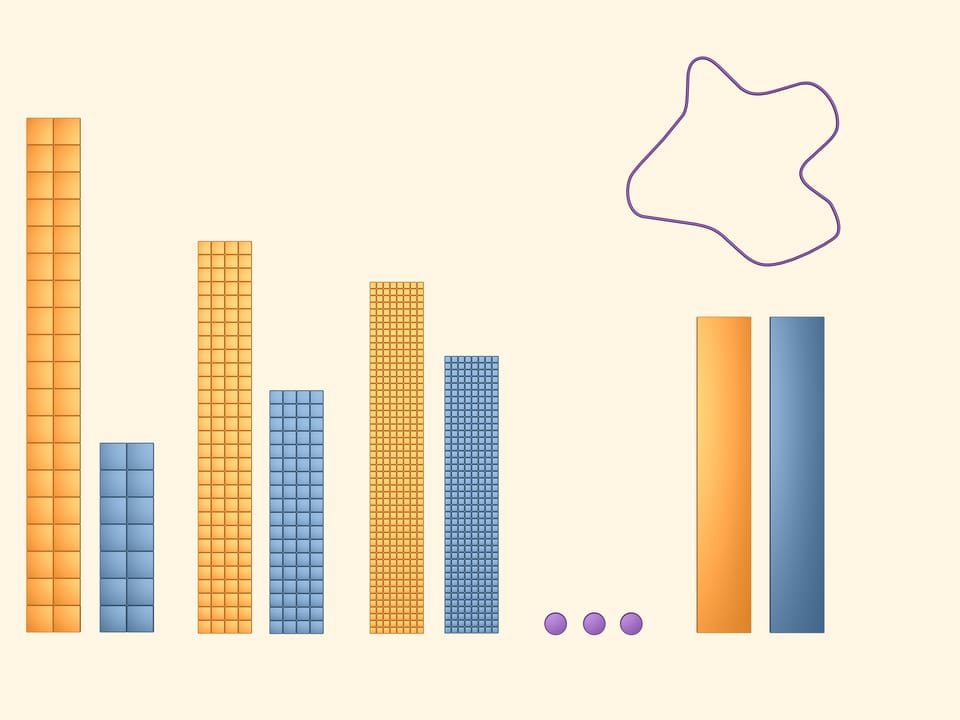
En considérant des réseaux de plus en plus fines, nous obtenons des limites supérieures et inférieures de l’aire cherchée de plus en plus précises.
Comme le réseau devient plu fin, l’aire de chaque carrés, dont il est constitué, tend vers zéro. Par une abstraction de la réalité, dans le modèle mathématique on dit qu’on peut faire des carrés aussi petits que l’on veux. Alors, on dira qu’à la limite le polygone jaune et le polygone bleu seront égaux. Nous allons considérer un rectangle, fait par les moitiés de ces rectangles jaune et bleu (on pourrait aussi bien considérer un seul de ces rectangles).
L’aire cherchée de la figure est par définition l’aire du rectangle en deux couleurs.
Dans la vie quotidienne il ya des cas où il est nécessaire de définir l’aire d’une figure approximativement. L’aire calculée, c’est à dire, doit être différente de la vraie au plus d’une quantité donnée. Pour résoudre ce problème, il faut prendre un réseau de carrés tels que la différence entre l’aire du rectangle jaune et l’aire du rectangle bleu ne dépasse pas le double de la marge d’erreur. Ensuite, comme l’aire de la figure, il faut prendre un nombre égal à la somme des aires des rectangles jaunes et bleus, divisé par deux.