Le cubisme est un courant avant-gardiste formaliste dans l’art figuratif européen du début du XXè siècle. Il tend à montrer la structure géométrique d’un volume. Les cubistes répartissaient la matière sur une surface plane ou l’assimilaient à des solides simples: sphère, cône, cube.
Defenition de The American Heritage Dictionary of the English Language: Quatrième édition. 2000
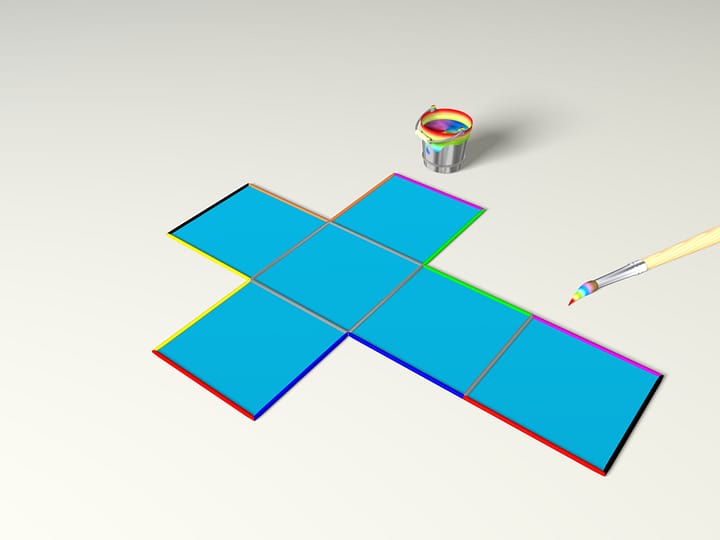
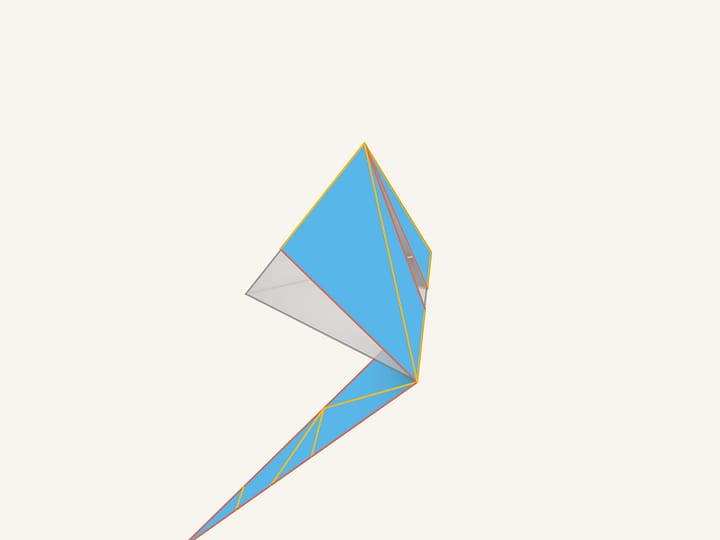
De combien de façons pouvons-nous découper un cube en carton suivant les arêtes, pour pouvoir placer les morceaux formés sur un plan? En géométrie, combien y a-t-il de développements pour un cube?
Il se trouve qu’un cube a 11 développements différents. Réfléchissez à la démonstration, pourquoi il n’y en a pas plus? Nous les verrons toutes dans les animations.
Il serait curieux que le parquet puisse être fait à partir de planchettes semblables aux développements d’un cube. Pour que la substitution de la surface soit du parquet, il faut obligatoirement que chaque point du plan se couvre d’un carré de parquet et qu’il n’y ait d’obturation, c’est-à-dire que chaque point soit recouvert exactement par un carreau.
Démontrons qu’on peut faire un parquet toujours identique, à partir des développements du cube suivant. Au début, nous ferons, à partir de carreaux dont l’aspect a été examiné, une bande (dans une direction unique), parfois avec des bords droits, mais le plus souvent, non. A côté de la bande obtenue, on peut en placer une autre identique, et ainsi, successivement paver toute la surface.