Le nombre de degrés de liberté est la quantité de paramètres indépendants, synonymes de l’état du système mécanique défini.
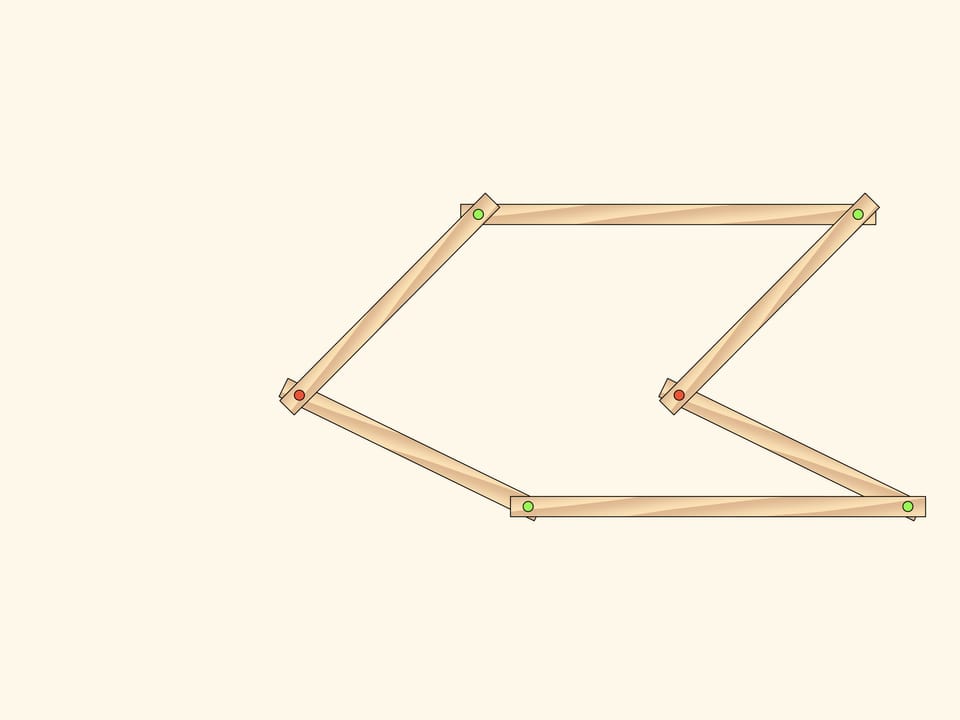
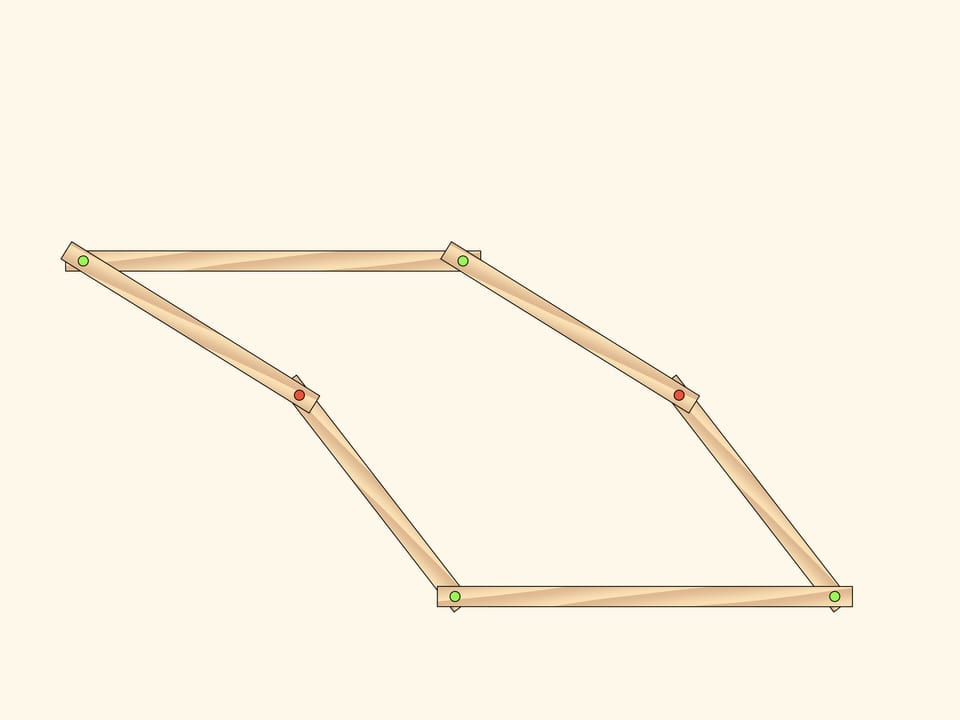
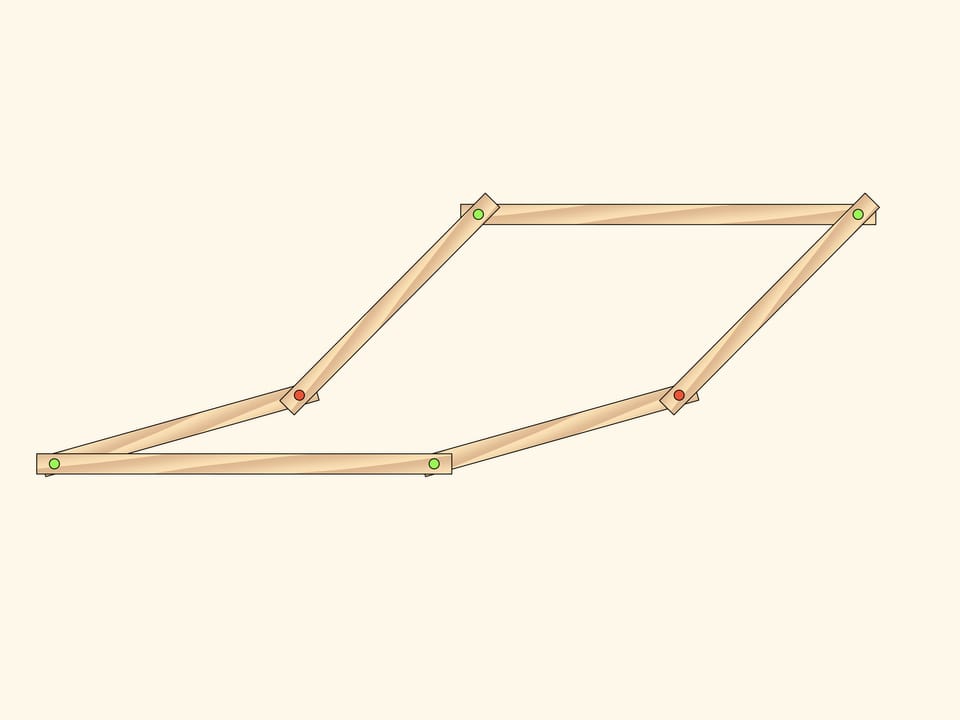
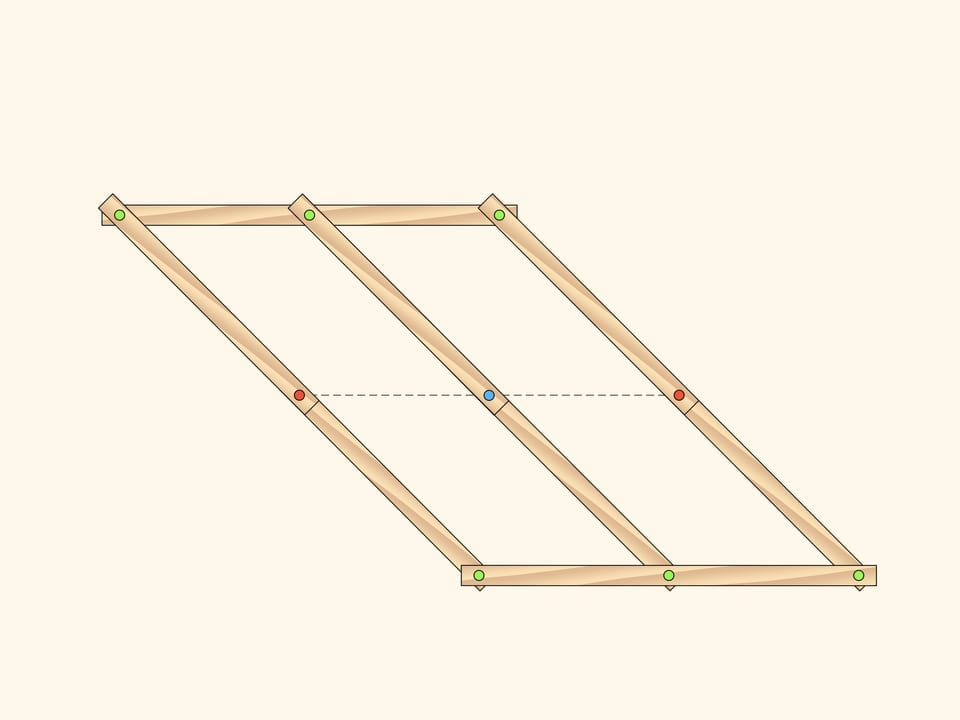
Observons un mécanisme à charnière plate, composé de deux parallélogrammes identiques, ayant deux charnières d’attache rouges en commun. Le nombre de marge de liberté d’un tel mécanisme est, évidemment, indifférent, ainsi, les parallélogrammes peuvent tourner, indépendamment l’un de l’autre, et comme paramètres, on peut, par exemple, choisir des angles de rotation des parallélogrammes, comptés à partir de l’horizontale.
Y a-t-il toujours, pour un mécanisme concret, fixé, un nombre de marge de liberté fixe? Ou existe-t-il des mécanismes dont le degré de liberté est variable? Il semblerait que ça existe…
Le premier mécanisme à charnière plate avec changement du degré de liberté a été imaginé par V. Vounderlich, en 1954. Il est fait de deux charnières renforcées et de douze maillons. Nous observerons un mécanisme plus simple de 9 maillons, créé par un mathématicien russe, Mikhail Kobalev.
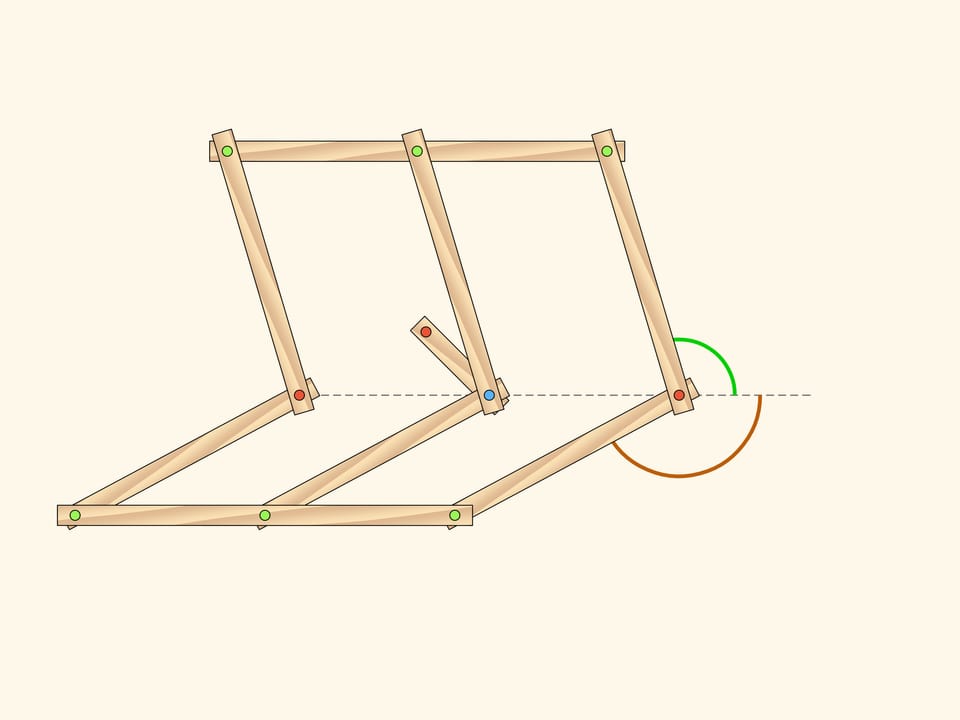
Ajoutons une ligne médiane au parallélogramme, et mettons un maillon court supplémentaire depuis les points d’intersection. Ce maillon se termine de l’autre côté, par une charnière d’attache rouge.
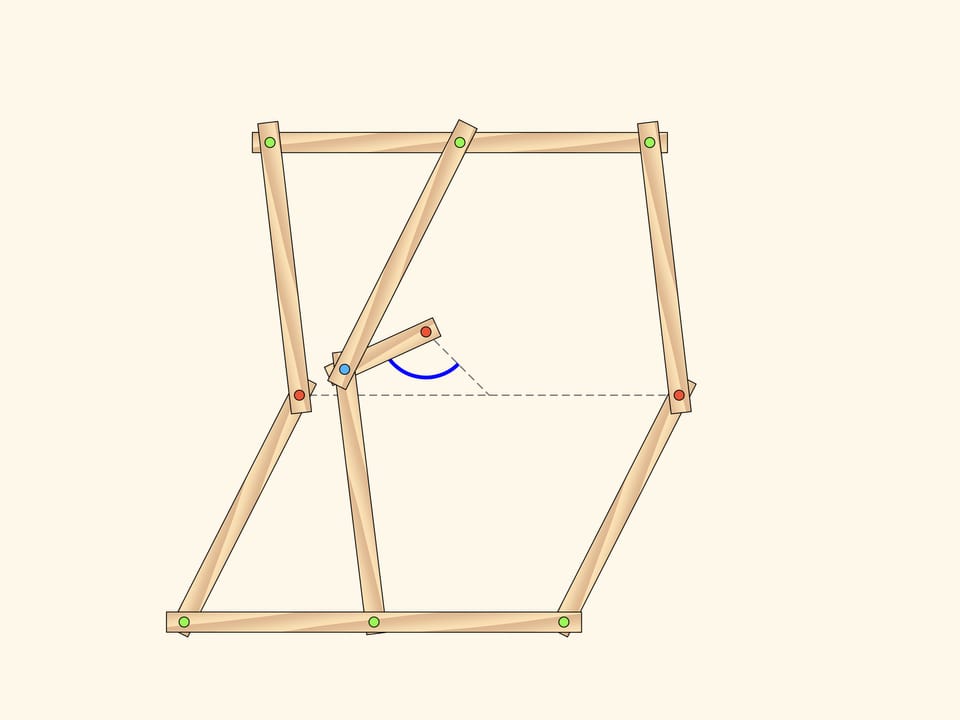
Tant que la charnière bleue reste sur la ligne médiane, reliant les deux charnières rouges fixes de départ, les maillons ajoutés n’apparaissent pas dans la quantité du degré de liberté du mécanisme. Sa disposition se compose, par exemple, de deux angles de détour des parallélogrammes, comptés à partir de l’horizontale.
Alors, la charnière bleue peut partir de la ligne médiane, au moment où la ligne médiane et le petit maillon sont sur une seule droite. Ainsi, seule la charnière bleue part de la ligne médiane, la situation de tout le mécanisme commence à se déterminer, ne serait-ce que par un paramètre! On peut choisir comme paramètre, un petit maillon ajouté et sa disposition à un moment donné.