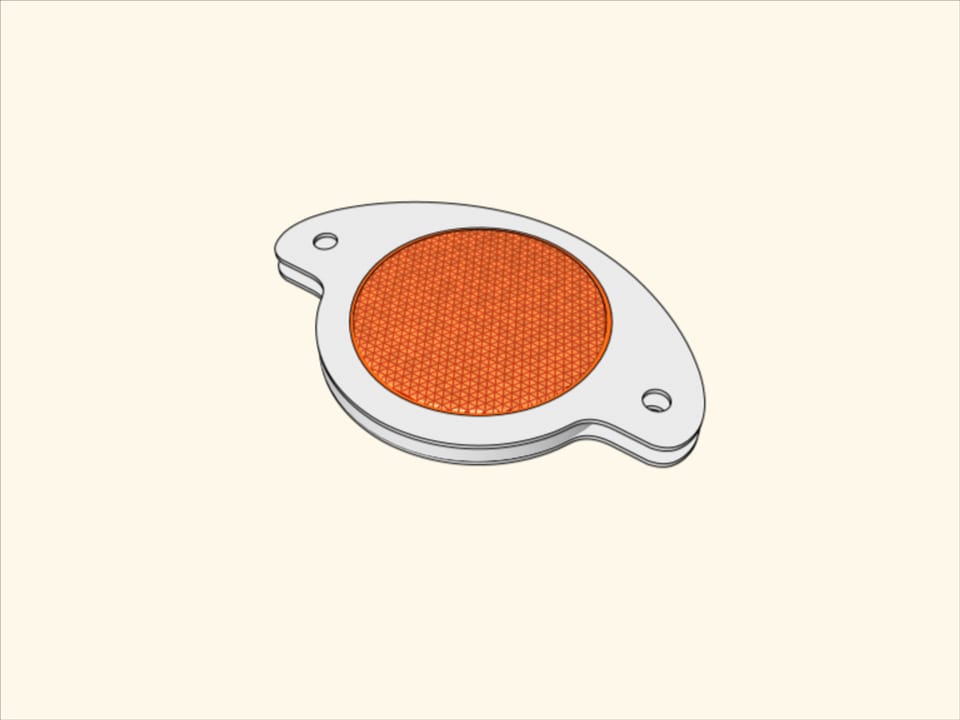
Chacun sait que dans les cataphotes des roues de bicyclette, il n’y a pas de source de lumière. Pourtant, lorsqu’un chauffeur passé à côté d’un cycliste, il voit le cataphote, au moment où ce dernier est mis sous la lumière des phares de sa voiture. Avez-vous déjà pensé qu’à ce même moment, les passants de derrière peuvent ne pas voir le miroitement du réflecteur? Il n’est pas surprenant que les caractéristiques du cataphote soient basées sur des faits géométriques simples.
On sait qu’en optique, le reflet d’un rayon à la surface d’un miroir se produit selon la loi d’égalité de l’angle d’incidence et de l’angle de réflexionю
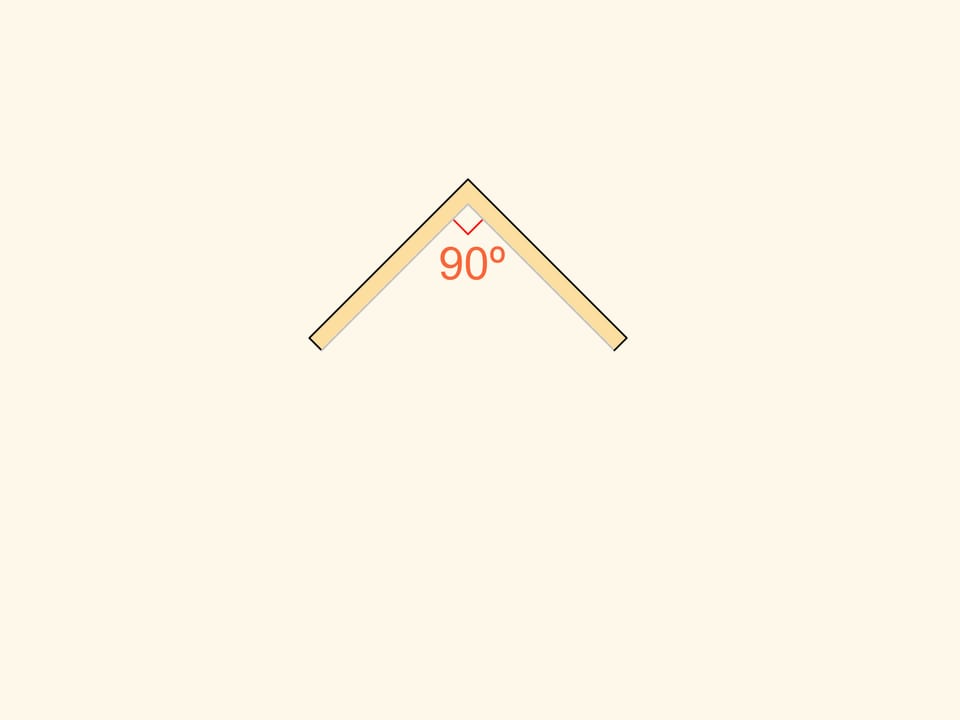
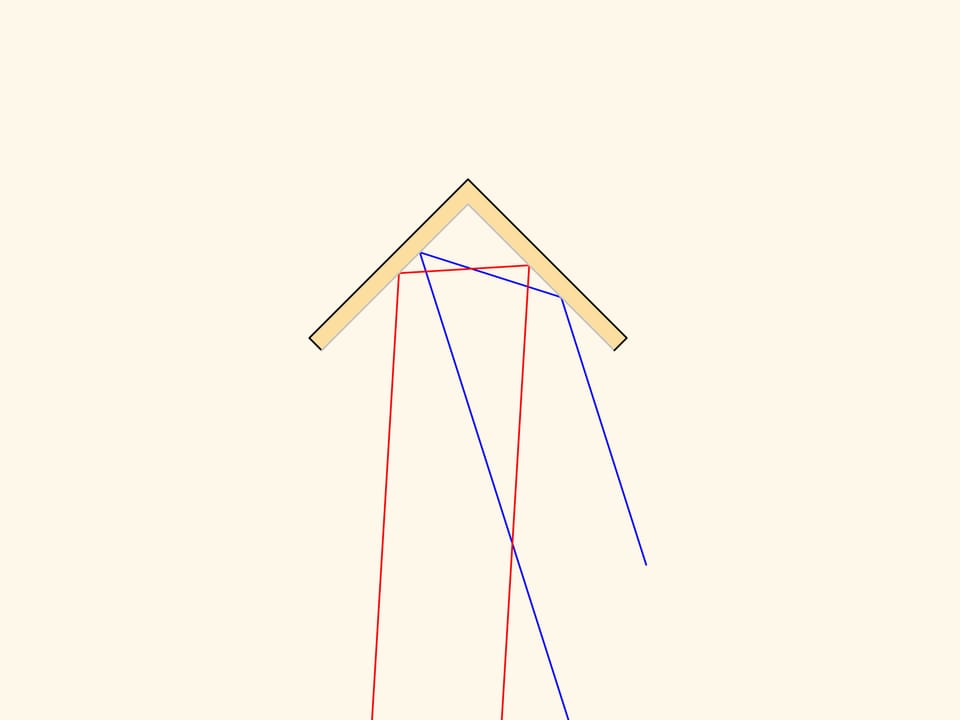
Considérons un cas basique: deux miroirs formant un angle de 90°. Un rayon allant sur la surface et atteignant un des miroirs. Après réflexion depuis le 2è miroir, le rayon va dans la même direction qu’initialement. Vérifiez cela, soit en calculant les angles, soit en analysant le reflet du vecteur du rayon.
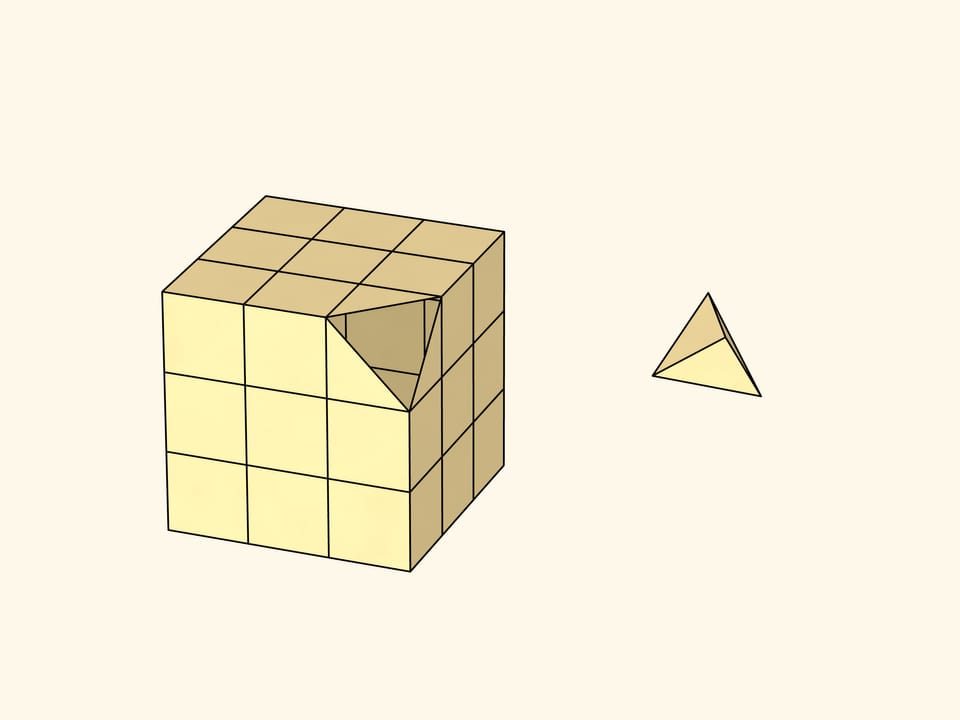
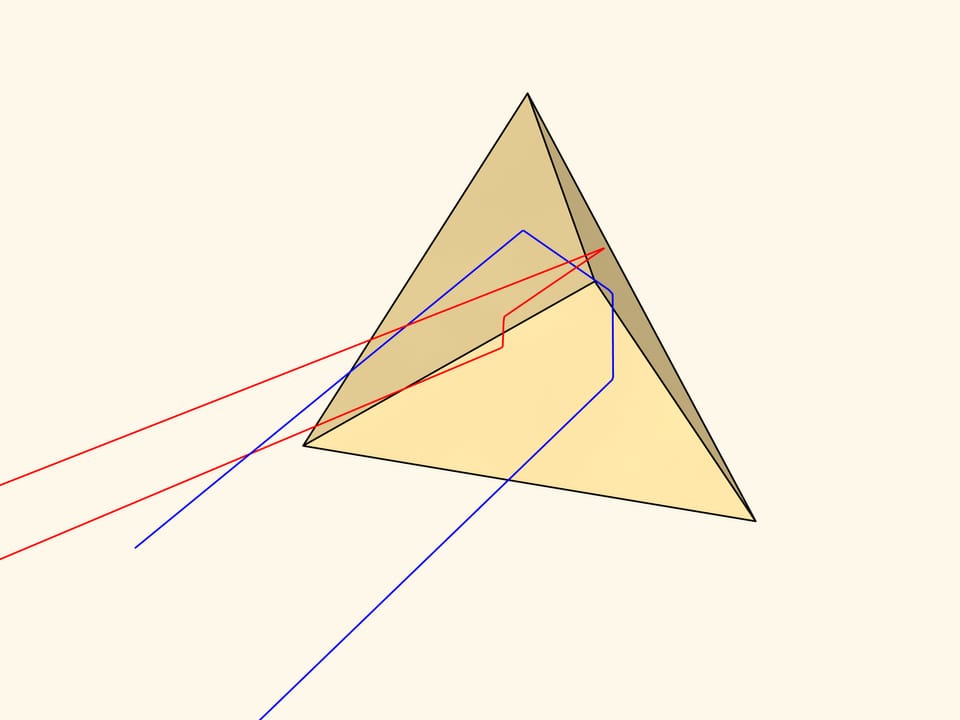
Pour obtenir le même effet dans notre 3D habituelle, il faut disposer 3 miroirs sur des plans identiques et perpendiculaires. Prenons l’angle d’un cube, dont l’extrémité forme un triangle équilatéral.
Le rayon, arrivant dans un tel système de miroirs, après réflexion des 3 plans, se dirige parallèlement au rayon arrivant dans la direction opposée. Vous pouvez le croire!
Justement, cette installation géométrique simple et sa propriété s’appellent: le réflecteur d’angles.
Pour l’application dans la technique, on fait de tels angles à une batterie, augmentant la surface de réflexion.
La compréhension des mathématiques simples aide à cette étape. Un plan peut être pavé avec des triangles, mais cela signifie que les réflexions angulaires sont plus facilement accollables.
C’est ainsi même qu’est construit un cataphote de vélo ou de voiture. Cependant, on utilise ces raisonnements géométriques dans la plupart des constructions technologiques.
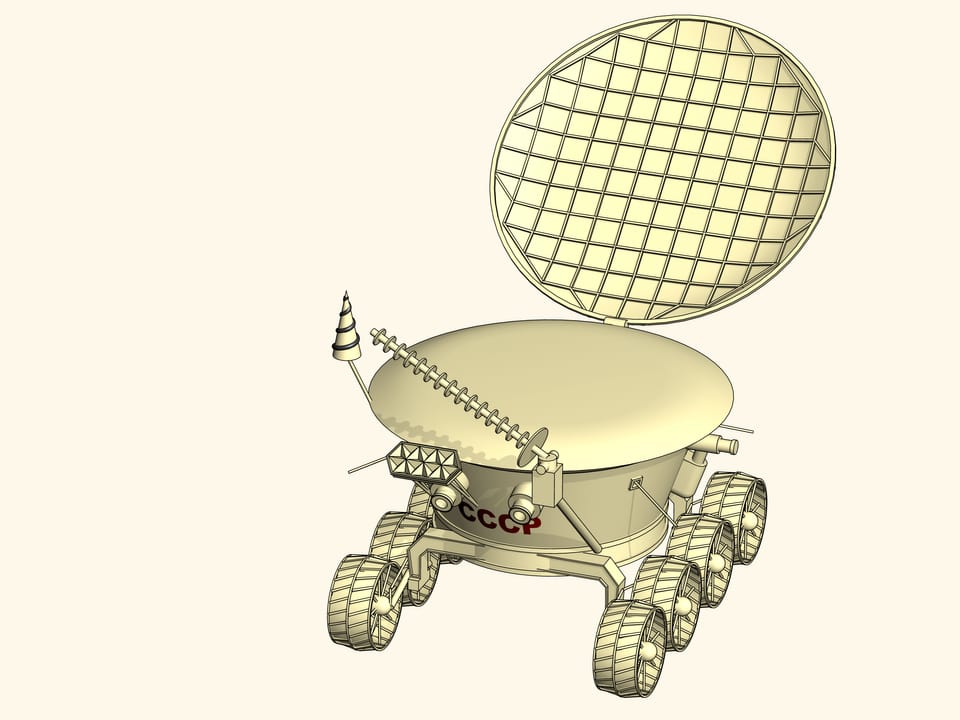
Le 17 novembre 1970, dans la région de la Mer de pluie, sur la Lune, une station a aluni, nommée par l’agence principale d’information du pays, l’agence télégraphique de l’Union soviétique (TASS), “Lune-17”. Un appareil soviétique s’est posé à la surface de la Lune, laissant la voie ouverte à un satellite de la Terre: Lunakhod-1.
Il est allé à bout des conducteurs depuis la Terre, qui pouvaient voir, par des caméras, une petite parcelle de la surface lunaire, devant un appareil.
Ayant compté sur le travail au cours de 3 mois terrestres, l’appareil a fonctionné 3 fois plus en 11 jours lunaires. La dernière séance de liaison, avec le premier Lunakhod, s’est effectuée le 14 septembre 1971. Pendant cette période, Lunakhod-1 a effectué une distance de 10, 540 km , en décrivant un cercle, et est revenu à son point de départ.
C’est surprenant, mais on avait fixé sur Lunakhod des réflecteurs angulaires. Tout d’abord, ils donnaient la possibilité à n’importe quel pays de vérifier l’existence d’un appareil soviétique sur la Lune. Et, le plus important, une telle installation géométrique simple aida la science à mesurer la surface de la Terre, depuis un satellite. Les chercheurs de tous les pays utilisent les réflecteurs angulaires de Lunakhod-1, même au XXIè siècle.
C’est ainsi que les réflexions géométriques protozoaires aident les gens, depuis la question de sécurité de la vie courante, jusqu’à la connaissance de l’univers.