Comment pouvez vous estimer la profondeur d’une station du métro, lorsque vous y accédez par un escalier mécanique? Il arrive que même pour répondre à cette question il peut être utile de connaître les mathématiques! En particulier, la trigonométrie.
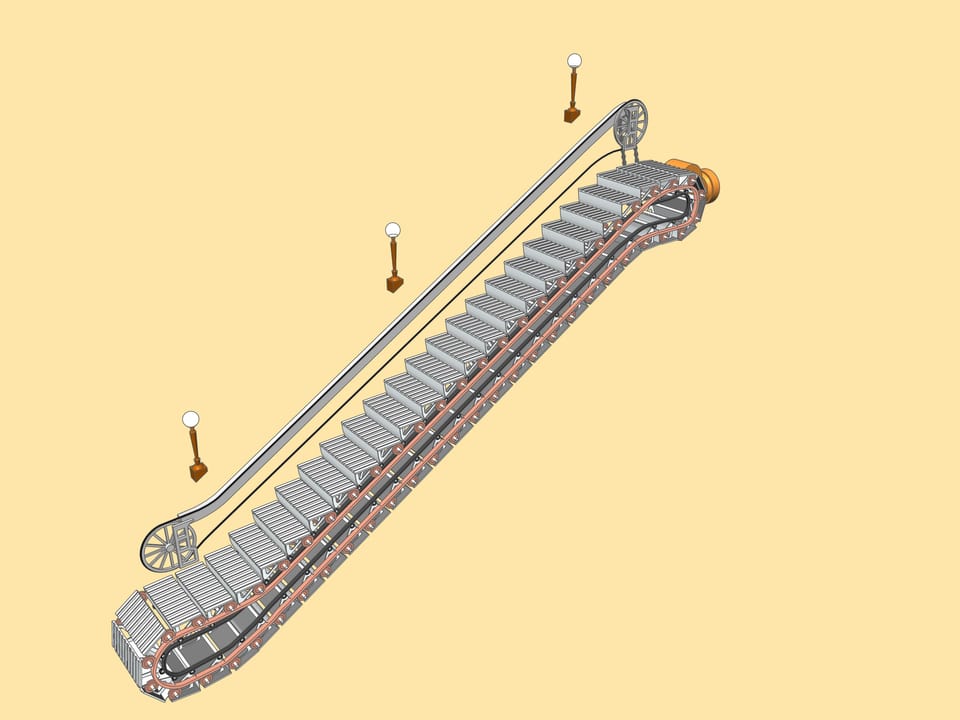
L’escalier mécanique du métro... Combien de choses sont cachées derrière ces mots, pour un observateur curieux. Une énorme machine en mouvement constant, un «escalier vivant»...
Tout a commencé vers la fin du XIXe siècle, lorsque le constructeur américain Jesse W. Reno (1861—1947) a breveté le premier «escalateur mobile». Dans sa construction, au lieu des marches fixées à une bande “infinie”, il y avait des cylindres longitudinaux. Mais le premier escalateur public a été fabriqué, selon son inventeur, Charles D. Seeberger (1857—1931), par l’usine “Otis” et a été exposé à l’Exposition universelle de Paris du 1900. Il avait des marches horizontales, sortant de sous une rampe sur une plateforme d’entrée et disparaissant sous la même rampe sur une autre plateforme : ce mécanisme donnait beaucoup de problèmes. En 1921, les deux idées — des marches horizontales et des cylindres — ont été mises ensemble pour construire un nouveau modèle, qu’à partir de ce moment, il a été toujours utilisé.
Lorsque dans les années trente, les russes commencèrent à projeter le métro de Moscou, ils ont essayé de faire usage de l’expérience étrangère. Cependant, le coût et le temps requis pour sa réalisation par les entreprises étrangères étaient si grandes que l’idée a été abandonnée. Alors le chef de la succursale londonienne de la société “Otis”, écrit ainsi au représentant du Conseil de Moscou: «Vos spécialistes sont des gens capables. Mais l’escalateur roulant est une affaire très compliquée, et ce problème n’est pas à votre portée. Même nous, avec nos décennies d’expérience, nous ne sommes pas en mesure d’exécuter le projet avec ces délais. Moi, comme un ami de l’Union Soviétique, j’ai le devoir de vous avertir que la date du début du métro peut ne pas être respectée». Mais les ingénieurs et les scientifiques soviétiques ont été capables de résoudre ce problème unique, et en Février 1935, un escalateur a commencé à transporter des passagers à la station de métro de Moscou.
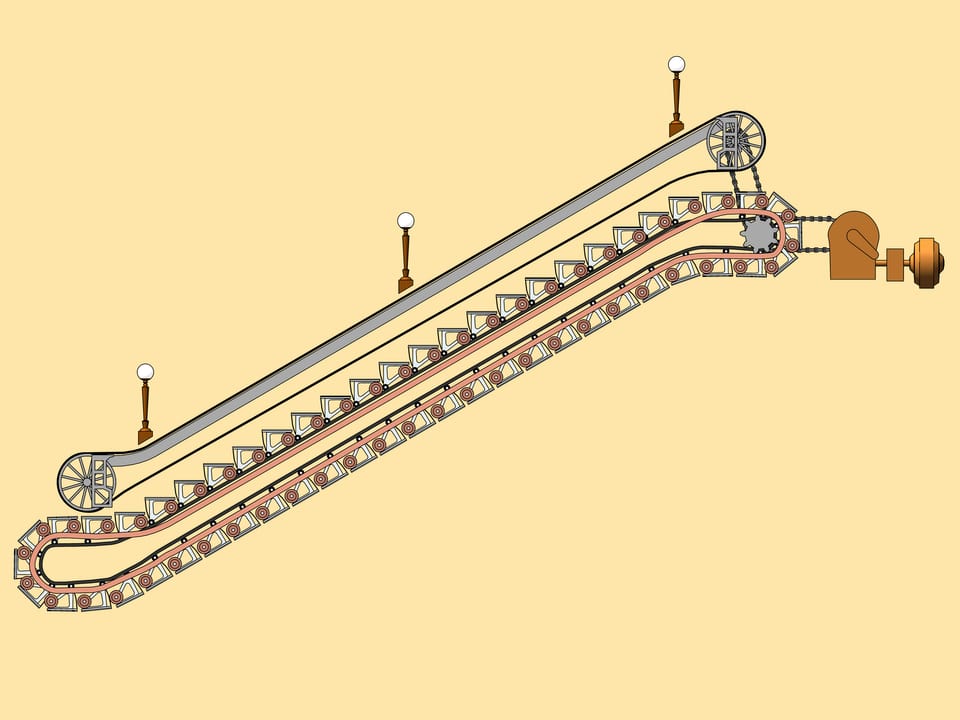
Un des éléments importants de l’escalateur est la marche. Elle a quatre rouleaux, deux petits et deux grands. Les grandes et les petites roulent le long de leur propres rails.
Lorsque les escalateurs furent conçus, même le choix des matériaux pour les rouleaux était un problème très important et difficile. Le métro de Moscou est ouvert de 6 heures jusqu’à environ une heure de la nuit. Autrement dit, plus que 19 heures — ce qui fait plus que 68000 secondes par jour. La vitesse minimale de fonctionnement d’un escalateur mécanique est de 0,75 m/s, ce qui signifie que chaque marche fait 50 km par jour. Et donc, jour après jour, sans arrêt, dans un an plus que 18000 km! Pouvez–vous imaginer quel genre de matériel devrait être utilisé pour les rouleaux, pour qu’ils tiennent sans de réparations et remplacements réguliers un nombre assez élevé de passagers qui montent sur les marches. Et ce n’est qu’un détail et un problème parmi tous ceux que les ingénieurs soviétiques devaient alors résoudre. Et de problèmes pareils in il y en avait des milliers.
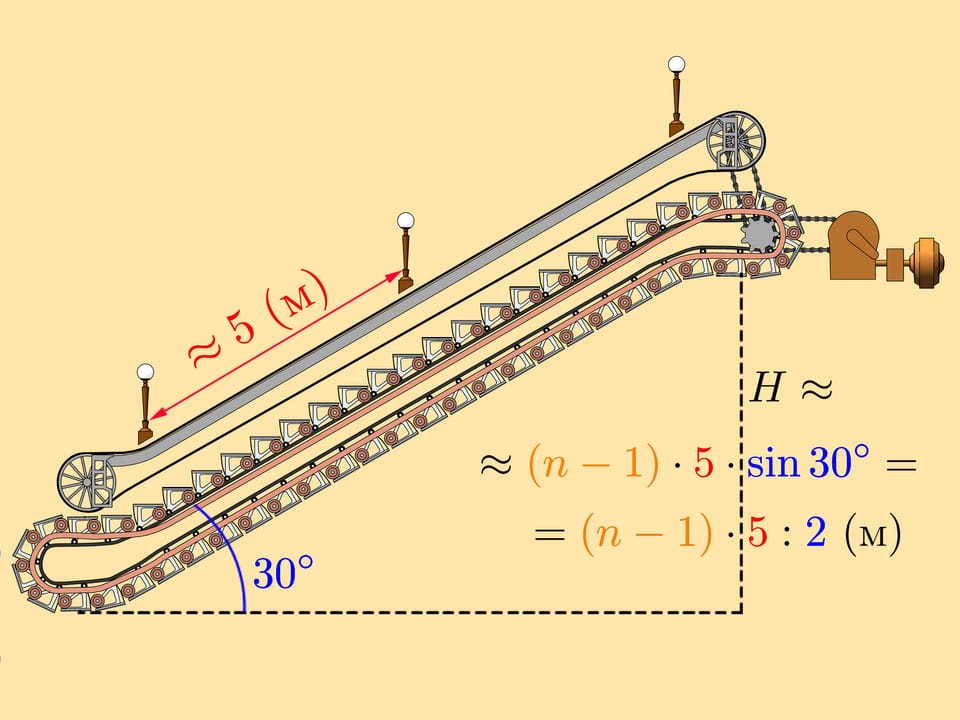
Voila le schéma d’un escalateur mécanique. Si l’on regarde de côté, on voit que la position mutuelle des rails, de gros rouleaux et de petits rouleaux, définit la propriété fondamentale de l’escalateur: dans la partie supérieure de «l’escalateur vivant», où sont les passagers, les marches sont toujours horizontales. Mais au dessous les marches sont inversés et deviennent parallèles aux rails, en économisant de l’espace dans le tunnel qu’ils parcourent.
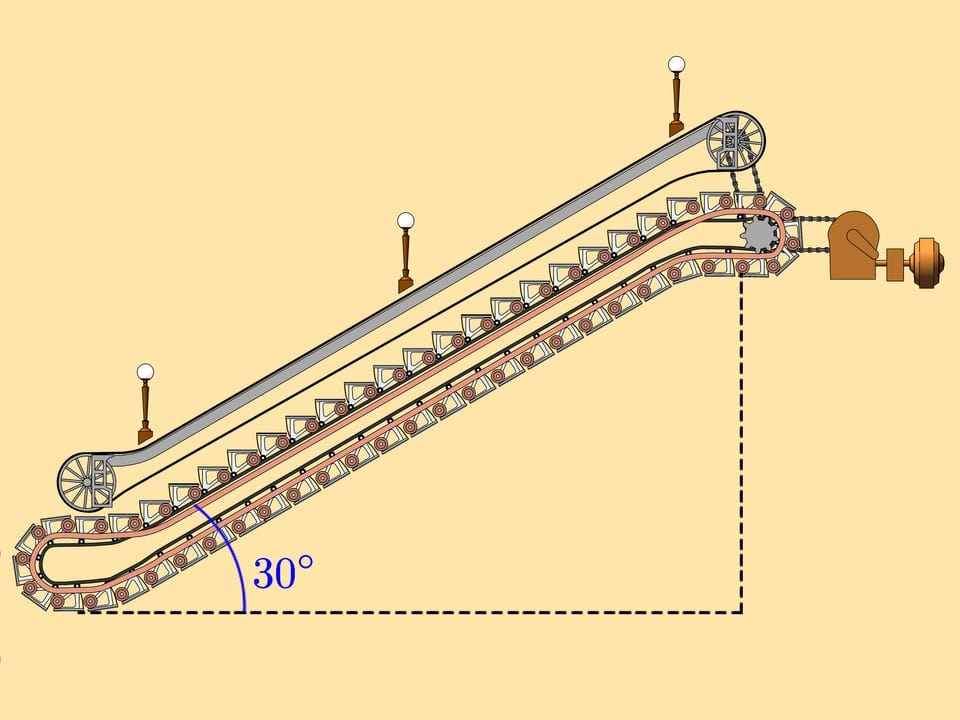
Mais revenons à notre question sur la profondeur, c’est–à–dire de combien de mètres on descend par l’escalateur. Le fait surprenant est que tous les escaliers mécaniques russes, dès premiers jusqu’aux actuels, sont inclinés de 30 degrés par rapport à l’horizontale!
Nous allons construire mentalement un escalateur sur un triangle rectangle. La longueur de son hypoténuse est la longueur de l’escalier, tandis que la longueur du cathète plus court est approximativement égale à la profondeur de la station de métro à laquelle cet escalateur conduit.
Mais comment calculer la longueur de l’escalier, lorsqu’on descend sur lui? On pourrait mesurer le temps, mais ensuite pour le calcul du parcours on devrait connaître exactement la vitesse de déplacement, qui peut varier de 0,75 m/s à 1 m/s, de sorte que l’erreur — d’un quatrième — est assez grand.
On pourrait calculer les mesures d’une marche, mais dans ce cas compter combien il y en a sur l’hypoténuse, tout en se déplaçant sur l’escalateur, c’est compliqué...
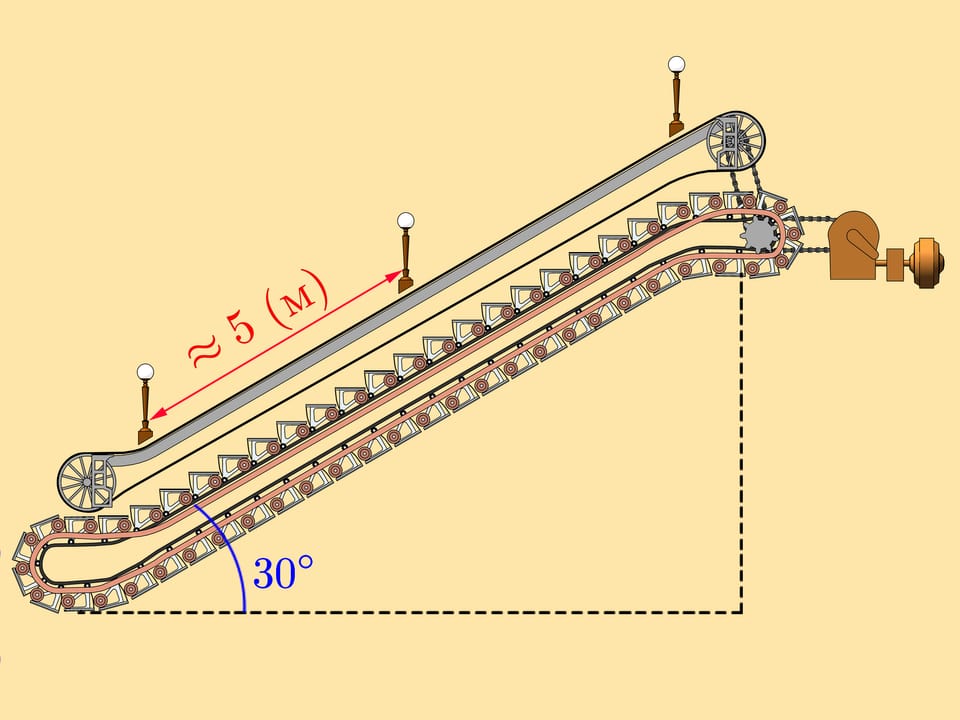
Que pouvons nous encore utiliser? En descendant ou en montant sur un escalateur mécanique, nous voyons continument des lampadaires! La distance entre eux n’est pas fixée, mais selon les règles du gouvernement, il faut un certain éclairage des tunnels. Il en résulte que les lampadaires sont situés à environ cinq mètres de distance l’un de l’autre.
En descendant par l’escalateur, on peut compter le nombre de lampadaires. Que devrions–nous faire alors, pour calculer la longueur de l’hypoténuse?
Ne vous précipitez pas à multiplier par 5. Pour le compte de la longueur nous n’avons pas besoin du nombre de lampadaires, mais de la quantité de distances entre eux! Du nombre de lampadaires il faut donc soustraire 1, et alors multiplier par 5 et par le sinus de 30°.
La chose jolie à ce point est que le sinus de 30 degrés est égale à ½, et avec ce nombre il est facile de faire le calcul! Donc, la formule obtenue pour la profondeur d’une station est très facile tant à retenir quant à être calculée.