Vous souvenez–vous de la forme du berlingot, le paquet de lait il y a cinquante ans? Il est surprenant que dans toute l’Europe, y comprise la Russie, on les achetait presque tous les jours pendant vingt ans, mais peux de gens rappellent exactement ce qui était écrit dessus.
Mais bien sûr tout le monde n’oublie pas que le paquet de lait avait la forme d’un tétraèdre (une pyramide triangulaire régulier). Les paquets en forme de tétraèdre ont été dans les années 40 du XXe siècle inventés par l’usine Tetra Pak, qui a pris le nom même de ces paquets. Les innovations apportées par Tetra Pak à cette époque étaient deux. Premièrement, pour la première fois des liquides alimentaires ont été placés dans des cartons. Deuxièmement, la production d’emballage tétraédrique était si facile qu’il était possible de les fabriquer directement dans les usines de lait.
Le paquet de lait plus fréquente dans l’Union soviétique était celui–ci.
Mais savez vous plier le morceau de carton par lequel le paquet de lait est fait afin d’obtenir un paquet de volume plus grand?
Mathématiquement parlant, il est possible de plier le développement d’un tétraèdre en obtenant un polyèdre avec un volume plus grand?
Un théorème de A. Aleksandrov dit qu’on ne peut pas le plier pour obtenir un polyèdre convexe avec un volume plus grand volume. Toutefois, il pourrait être possible d’obtenir un polyèdre non convexe avec plus de volume.
Aussi étrange que cela puisse paraître, c’est effectivement possible!
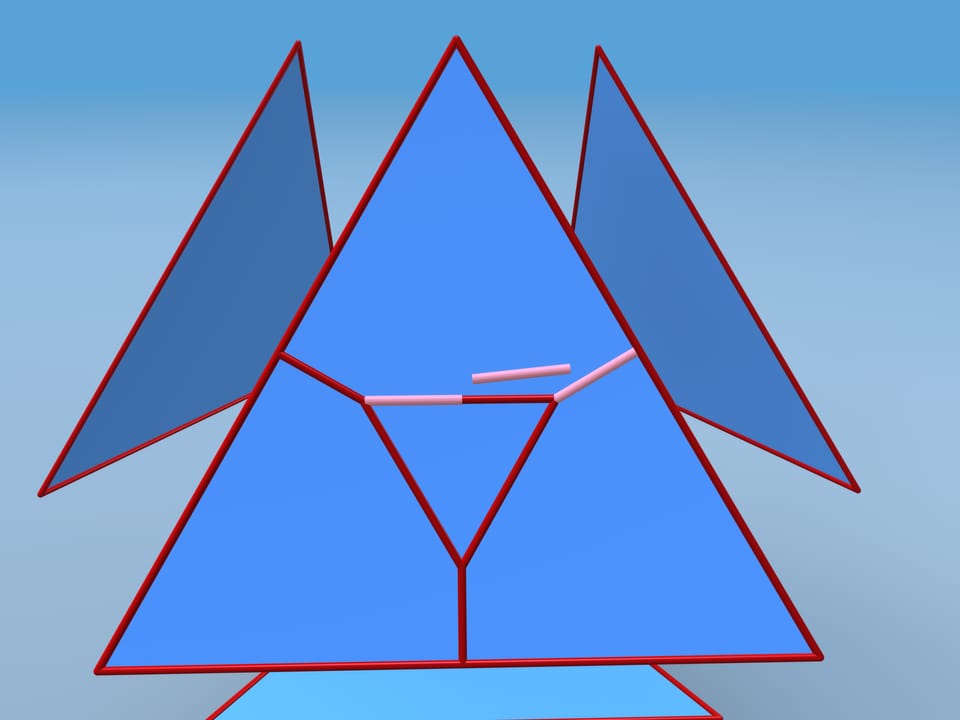
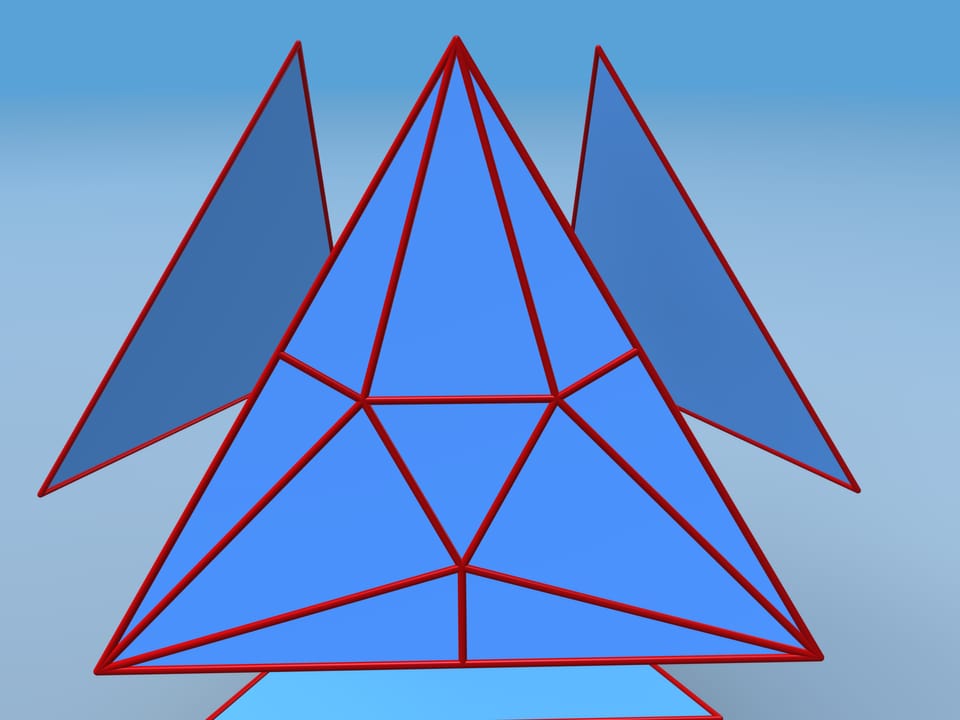
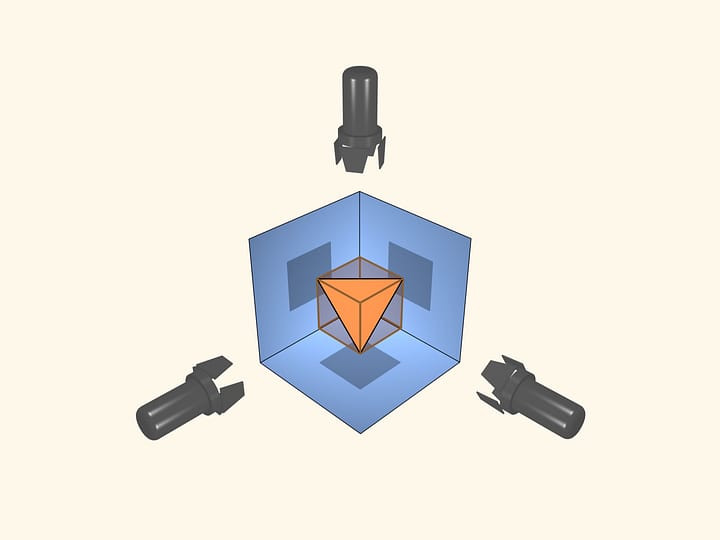
Nous allons suivre la construction que David D. Bleecker a suggéré en 1996. Eloignons les faces les unes des autres et ajoutons de nouveaux sommets et arêtes comme il suit. Prenons dans le centre de chaque face un triangle équilatéral avec les côtés longs deux fois la distance entre le sommet et le côté de la face. En suite nous dessinerons les arêtes supplémentaires.
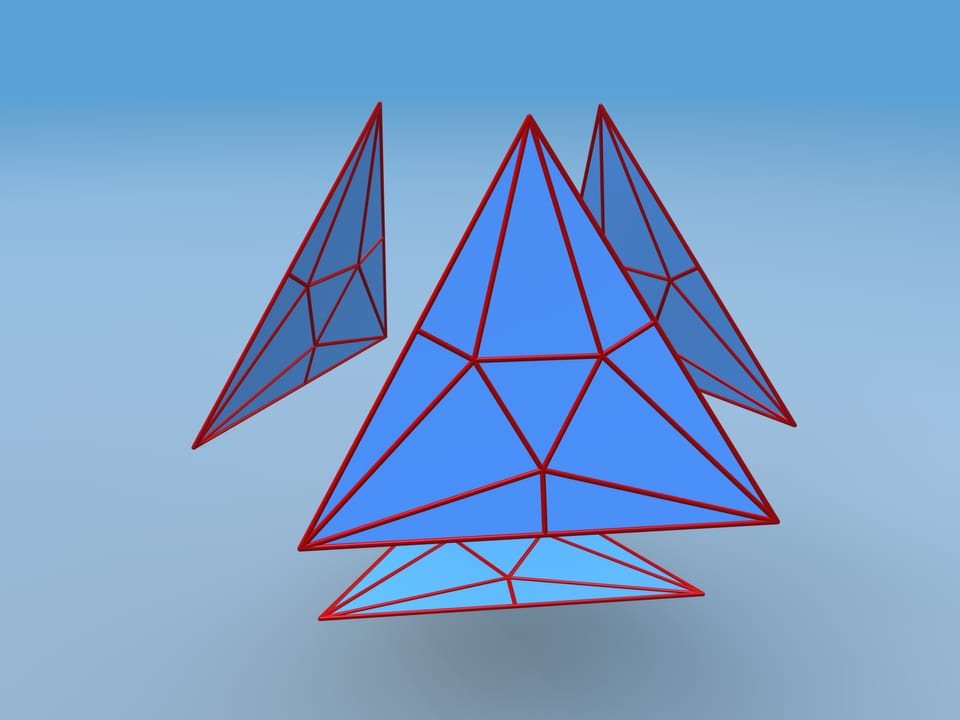
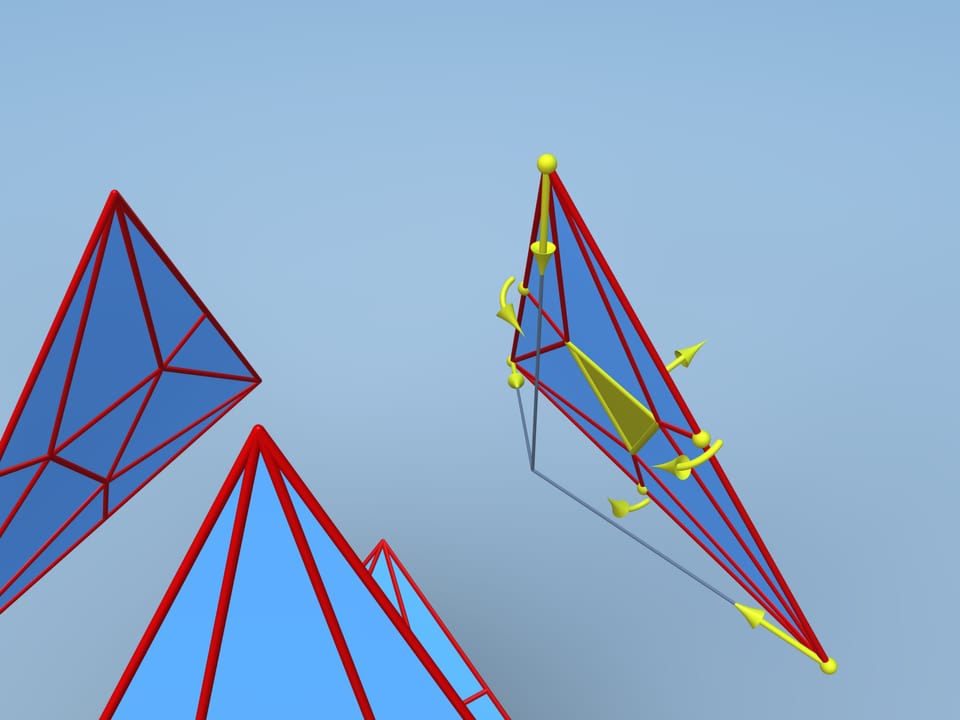
Répétons la même procédure sur chaque face. Replions chaque face le long des arêtes de telle sorte que ses sommets et les milieux des côtés vont se déplacer vers le centre du tétraèdre, tandis que le triangle au centre restera éloigné. Attachons ensemble les quatre parties. Quelques–unes des faces nouvelles sont coplanaires ainsi que les arêtes qui les séparent disparaissent.
Pour calculer le volume de ce polyèdre, nous allons le diviser en morceaux. Notre polyèdre est composé de 4 pyramides identiques hexagonales et d’un tétraèdre avec les sommets tronqués. Pour simplifier le calcul, attachons quatre petits tétraèdres au tétraèdre tronqué, après nos soustrairons leur volume du volume total du tétraèdre.
Nous découvrons ainsi que le volume du polyèdre est le 37,7% plus grand que celui du polyèdre initial. Ainsi, le morceau de carton par lequel on a fait l’emballage tétraédrique peut être plié en un paquet plus d’un tiers plus grand!
Étonnamment, le tétraèdre ne constitue pas une exception. Il s’avère que le développement de tout polyèdre convexe à faces triangulaires peut être plié dans un polyèdre avec un volume plus élevé. Ce théorème a été démontré par D. Bleeker en 1996, qui a également proposé un algorithme pour le faire.
Dans son article, D. Bleecker a considéré, ainsi que des polyèdres avec des faces triangulaires, deux polyèdres qui n’appartiennent pas à cette classe: le cube et le dodécaèdre. Aussi leurs développements peuvent être pliés en polyèdres non convexes qui contiennent plus de volume.
Conjecture
Le développement de tout polyèdre convexe peut être replié en vue d’obtenir un polyèdre non convexe avec plus de volume.
Questions ouvertes
Prouver (ou infirmer) la conjecture.
De quelle quantité peut augmenter au maximum le volume du polyèdre obtenu par le pliage du développement d’un tétraèdre?