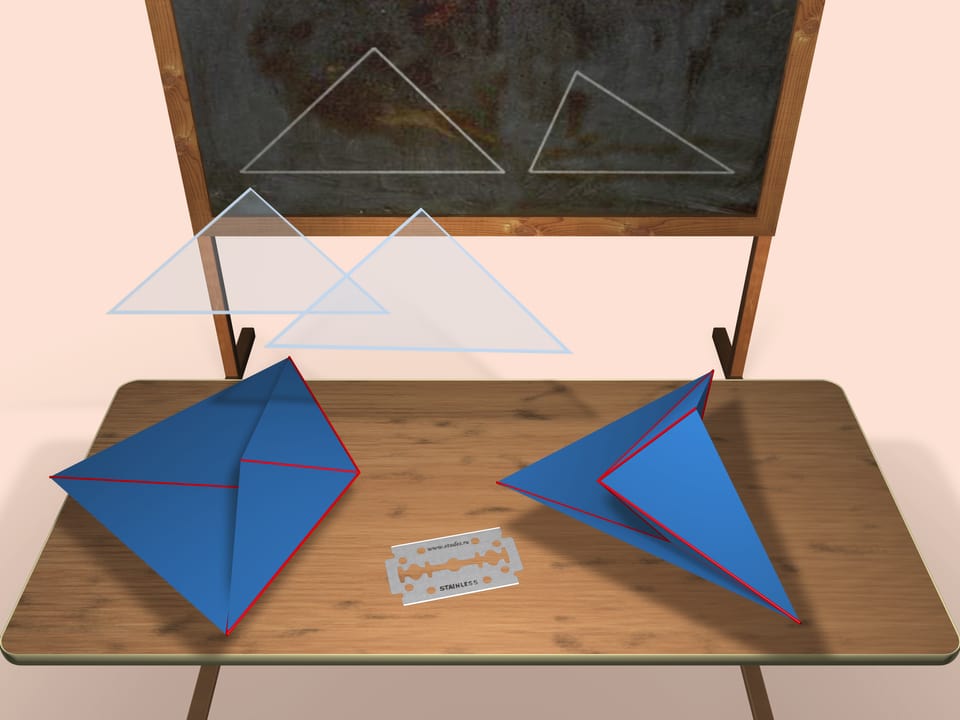
Est-il possible de faire un polyèdre convexe et un concave à partir d’un seul pan? Bien sûr, c’est possible, direz-vous. Un des exemples est présenté sur le dessin.
On a réussi à faire un polyèdre convexe et un concave d’un assemblage de pans. Lequel des deux aura un volume supérieur?
Il se trouve qu’on peut trouver des pans pour que le volume d’un polyèdre concave soit plus grand que le volume d’un polyèdre convexe, composé de ces mêmes pans. Le film illustre cet exemple.
Considérons deux triangles (les longueurs exactes des côtés seront indiquées à la fin du film) dont les pans seront ceux des futurs polyèdres. Comme nous le voyons, chaque triangle deviendra, en même temps, un pan pour les deux polyèdres. Ce polyèdre, construit à gauche, sera convexe, celui de droite, concave.
Les deux polyèdres construits sont des octaèdres (bien que non-réguliers). Leur hauteur est de 6 et leur base, de 8.
Qu’est-ce que le volume d’un corps, d’un polyèdre, dans l’idée générale? C’est la quantité de liquide que peut contenir ce polyèdre. Otons les sommets et versons de l’eau, à l’intérieur de chaque polyèdre. Le polyèdre convexe est déjà plein, et le concave, pas encore. L’eau s’est peut-être écoulée à une vitesse différente. Pour comparer correctement les volumes, transvasons le liquide de chaque polyèdre dans un verre identique. Le niveau de l’eau dans le verre de droite est supérieur à celui de gauche. Cela signifie que le volume du polyèdre concave est effectivement supérieur au volume du polyèdre convexe.
Si nous calculons attentivement, nous verrons que le rapport volumique entre le polyèdre concave et le convexe est égal à 1,163.
Dans notre problème, on doit examiner précisément le rapport volumique, et non la différence des volumes. Le fait est que le rapport ne dépend pas de la taille des triangles de départ, utilisés comme face pour la construction des polyèdres.
Concernant l’exemple observé, le volume du polyèdre concave construit est supérieur de 16% au volume du polyèdre convexe. Vous pouvez vous-mêmes réaliser les polyèdres donnés, en utilisant les faces pour les côtés indiqués.
On place les centres des octaèdres comme origine, et on effectue une rotation appropriée, les coordonnées des sommets seront alors présentées dans le film.
L’exemple de construction de deux polyèdres, présenté dans le film, a été proposé par S. N. Mikhalev, en 2002, pendant sa thèse à la faculté de mathématiques-mécanique de MGU.
C’est le meilleur des exemples connus (avec un rapport volumique maximal connu de polyèdres). Cependant, on ne sait pas, jusqu’à présent, quel peut être le rapport volumique maximal des volumes des polyèdres concaves et convexes, composés de ces mêmes faces. Cette question attend toujours son investigateur!