On dit de l’orbite d’un satellite qu’elle est géostationnaire si, pendant la révolution de la Terre, le satellite est toujours suspendu à un même point au dessus de la surface terrestre. Ces orbites sont souvent utilisées pour le système de communication et de positionnement.
Le satellite que vous observez sur l’image apparaît comme le symbole du programme spatial de notre pays. C’est Soiuz-TM.
Et voilà qu’à un moment donné, est apparue la force du programme “Vremia”, les principaux programmes d’informations TV du pays.
Mais dans l’animation, nous voyons comment se produit le processus d’émission s’un signal, par exemple, d’un satellite actuel de télévision.
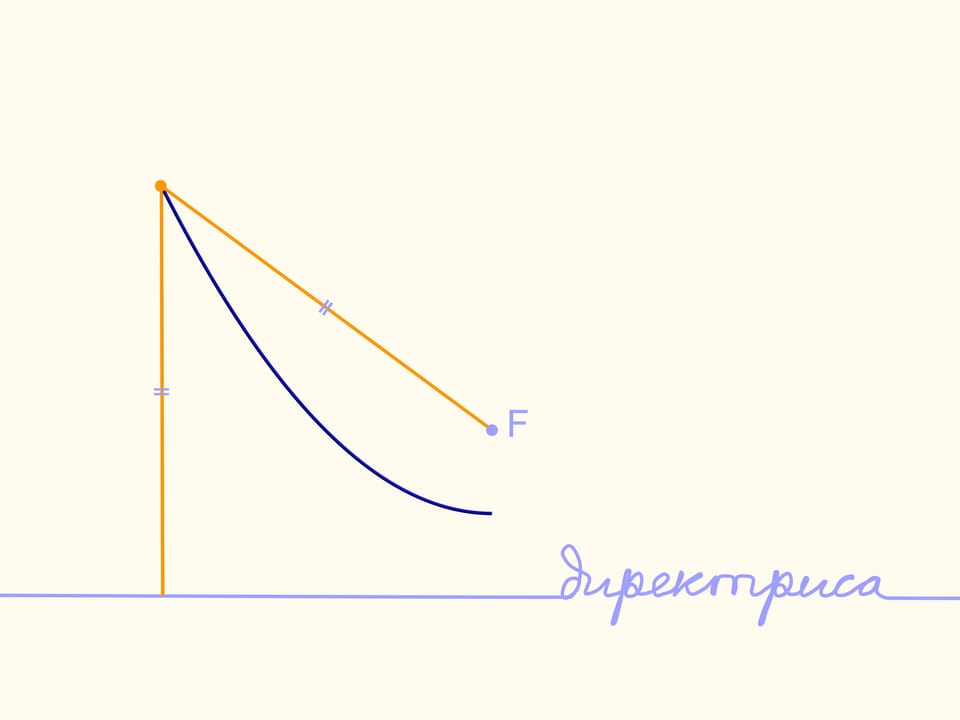
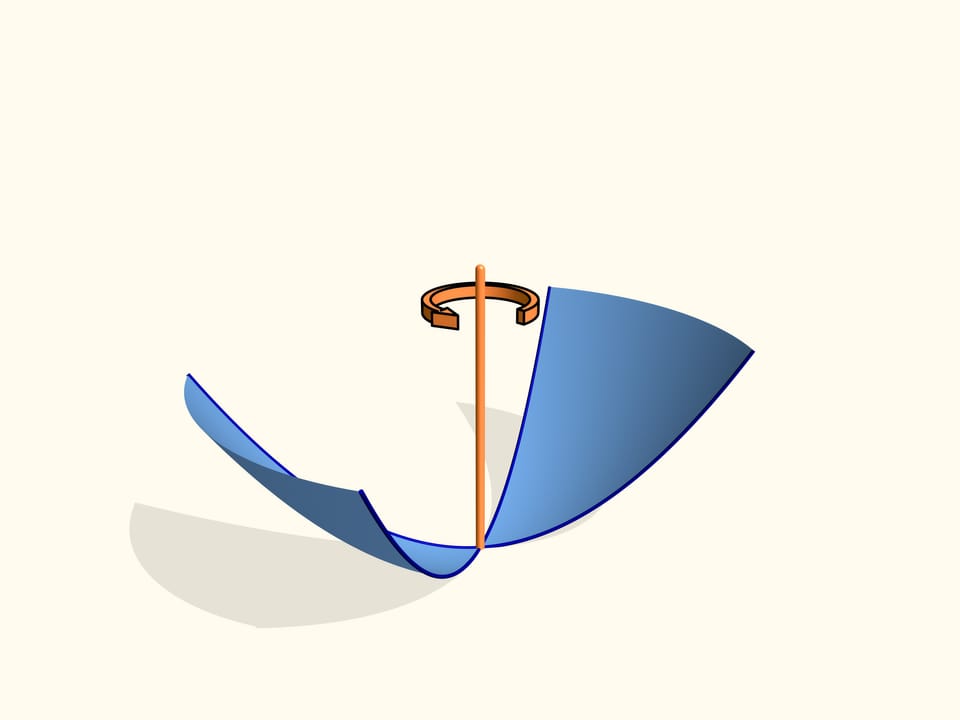
Nous faisons passer une droite et l’appelons directrice. Prenons un point de cette droite. L’emplacement géométrique des points, d’éloignement égal à la directrice et au point donné (appelé foyer), s’appelle parabole.
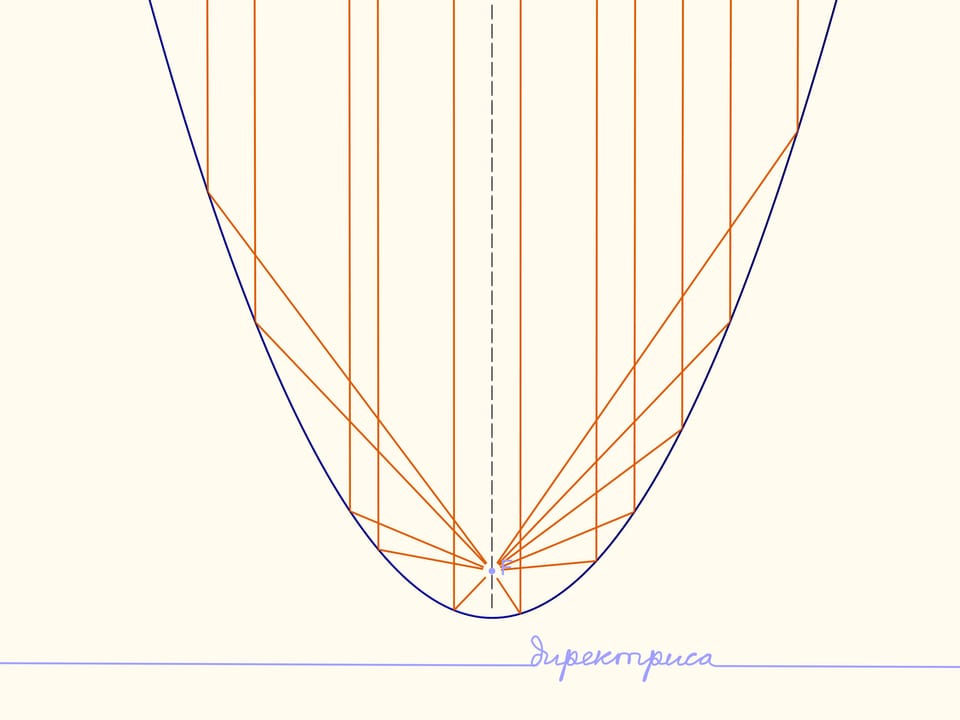
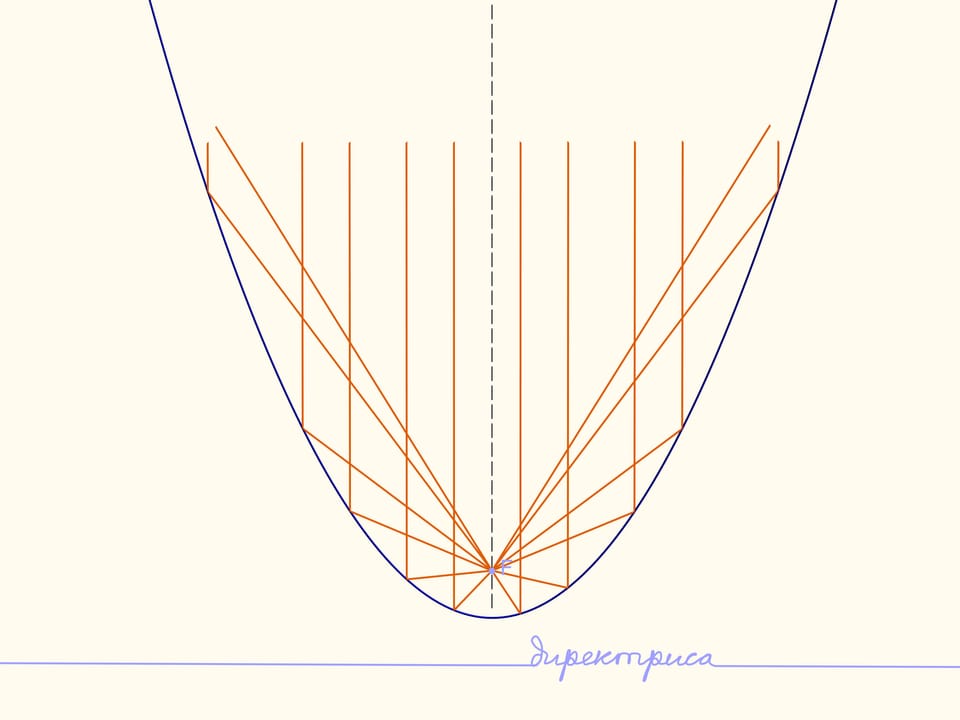
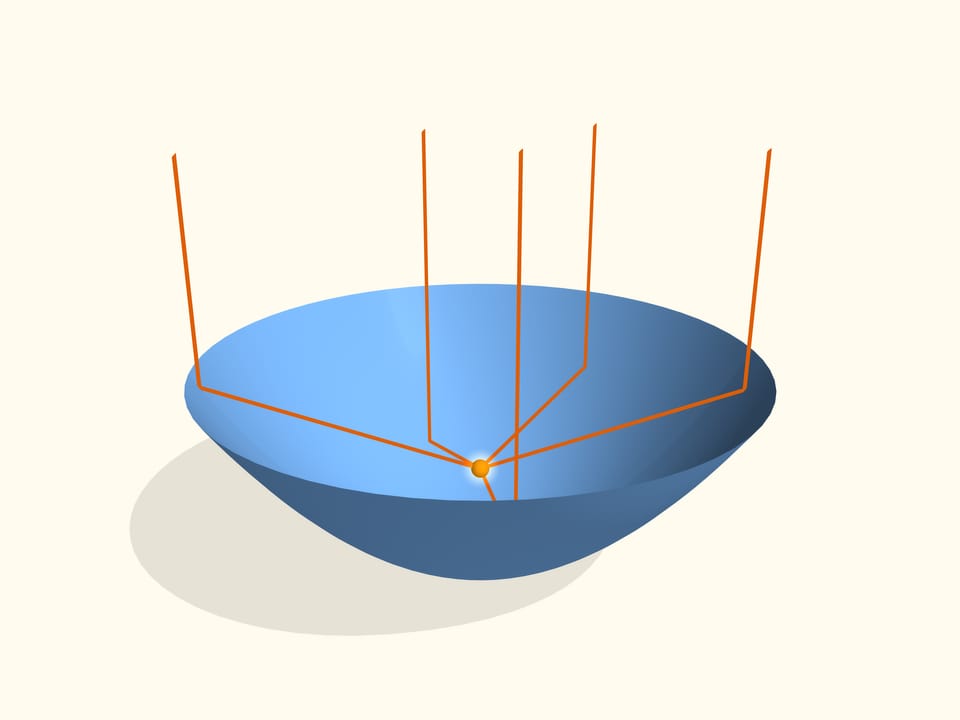
Si on dirige des rayons de lumière sur la parabole, alors, à son axe de symétrie, tous les rayons se rassembleront sur le foyer de la parabole. Cette propriété s’appelle la propriété optique d’une parabole.
C'est certainement vrai à l’inverse. Si on remplace le foyer par une lampe, alors, les rayons reflétés par la parabole sont parallèles et la directions de la lumière est droite. Si on fait tourner la parabole selon son axe de symétrie, on obtiendra alors une surface de rotation de deuxième ordre, une paraboloide.
Puisque pour n’importe quelle section du plan existe un axe de symétrie, il y a une et une seule parabole, alors la propriété optique est valable pour une paraboloïde. Si on remplace le foyer d’une paraboloïde par une lampe, alors, les rayons reflétés par la surface seront parallèles les uns aux autres. C’est également valable à l’inverse.
On utilise justement cette propriété pour les antennes satellites paraboliques. Comme un satellite se situe très loin des antennes, on peut considérer que les rayons sont presque parallèles et le poste de signal se situe au foyer de la paraboloïde.