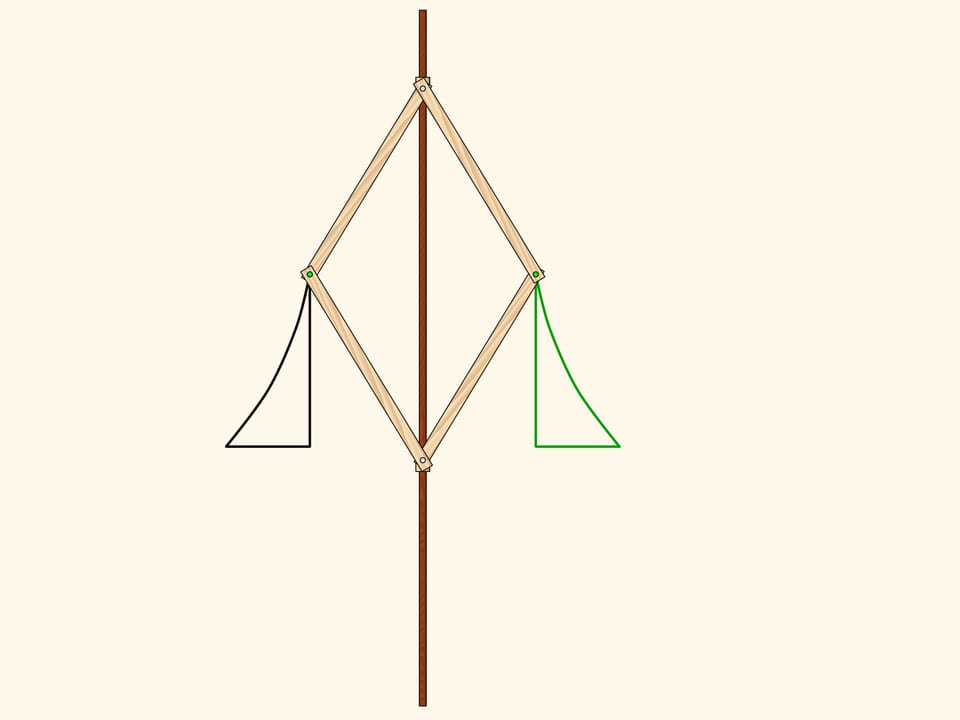
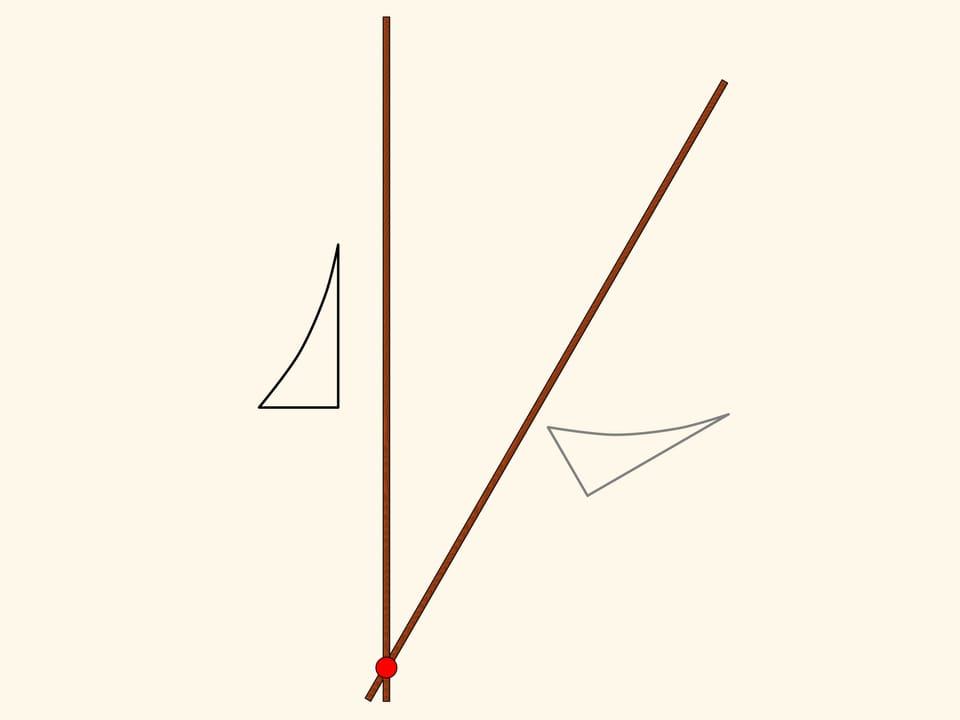
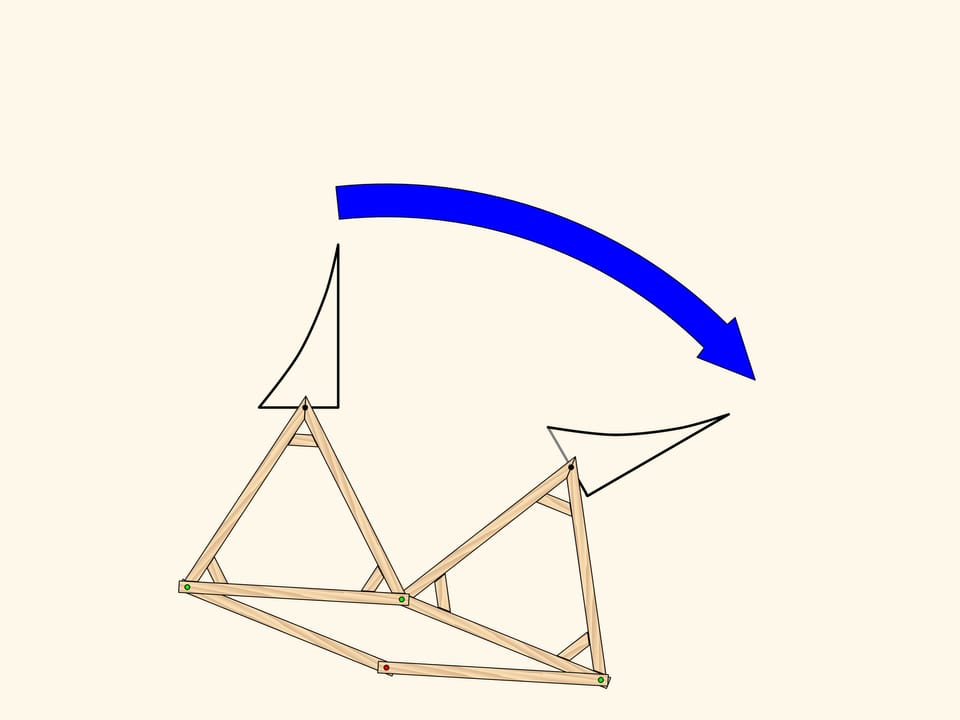
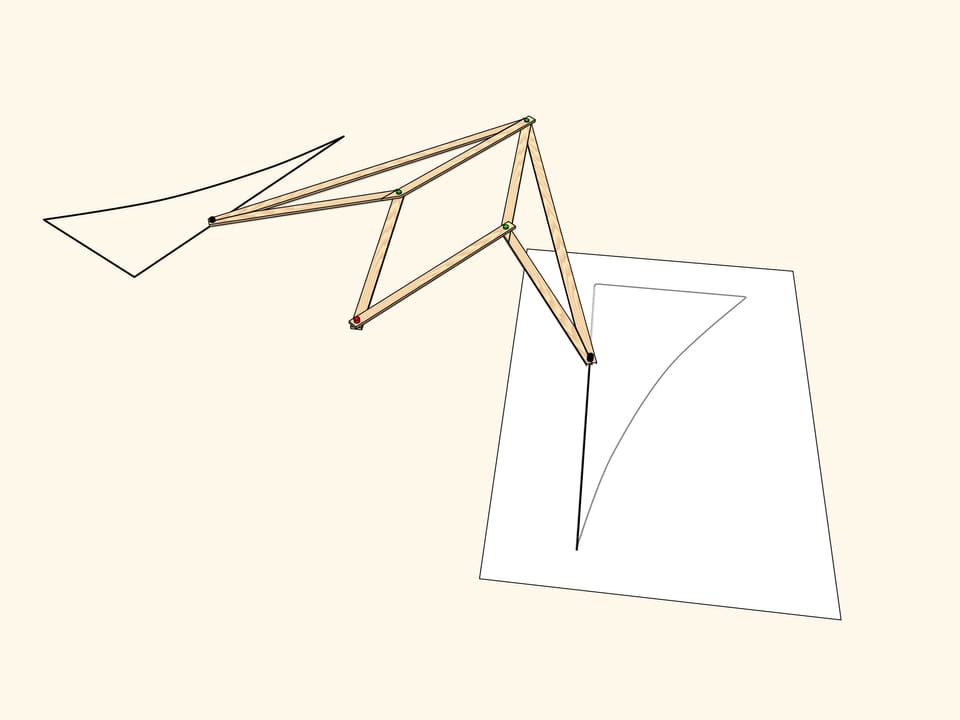
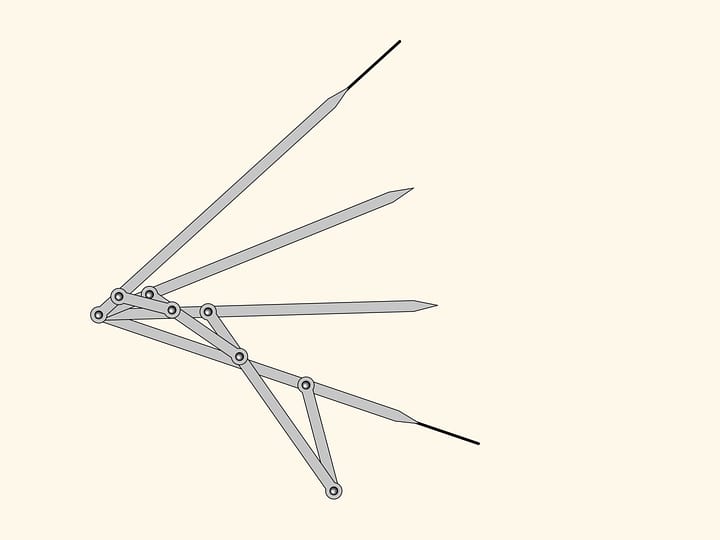
Pour réaliser la réflexion par rapport à un axe, nous utilisons un losange à quatre charnières, composé de quatre barres de même longueur et avec deux sommets opposés qui se déplacent le long d’un axe fixe (en rouge). En fait, la position de l’une des deux charnières libre (en vert), détermine la longueur du côté opposé du triangle, don elle est le sommet, et ce triangle résulte être égale à celui de l’autre coté de l’axe, donc les deux charnières en vert du mécanisme sont toujours dans des positions symétriques par rapport à l’axe.
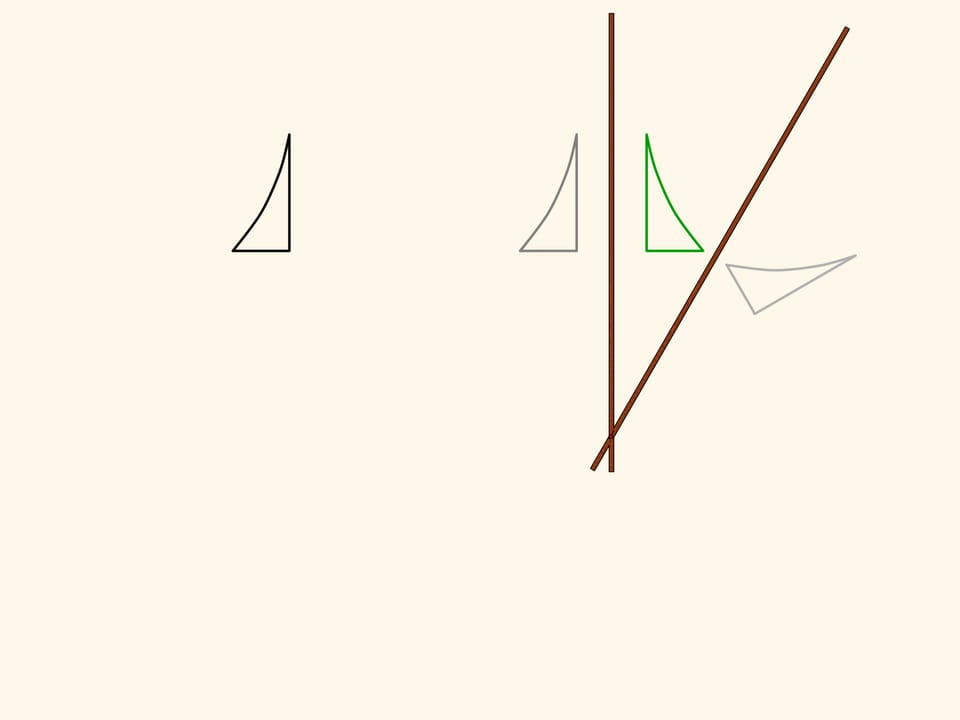
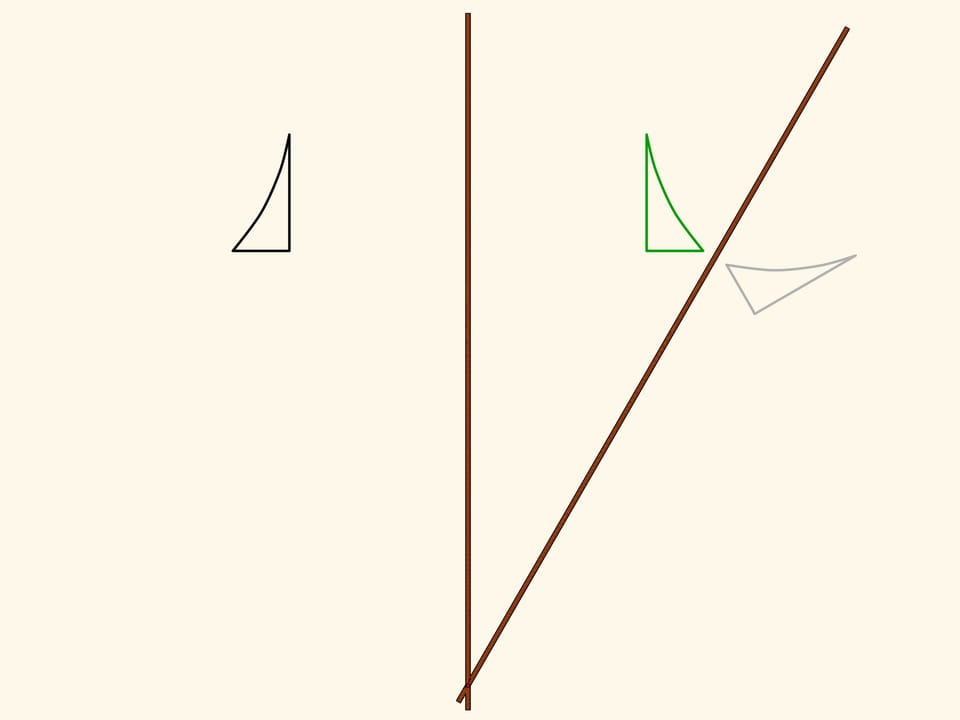
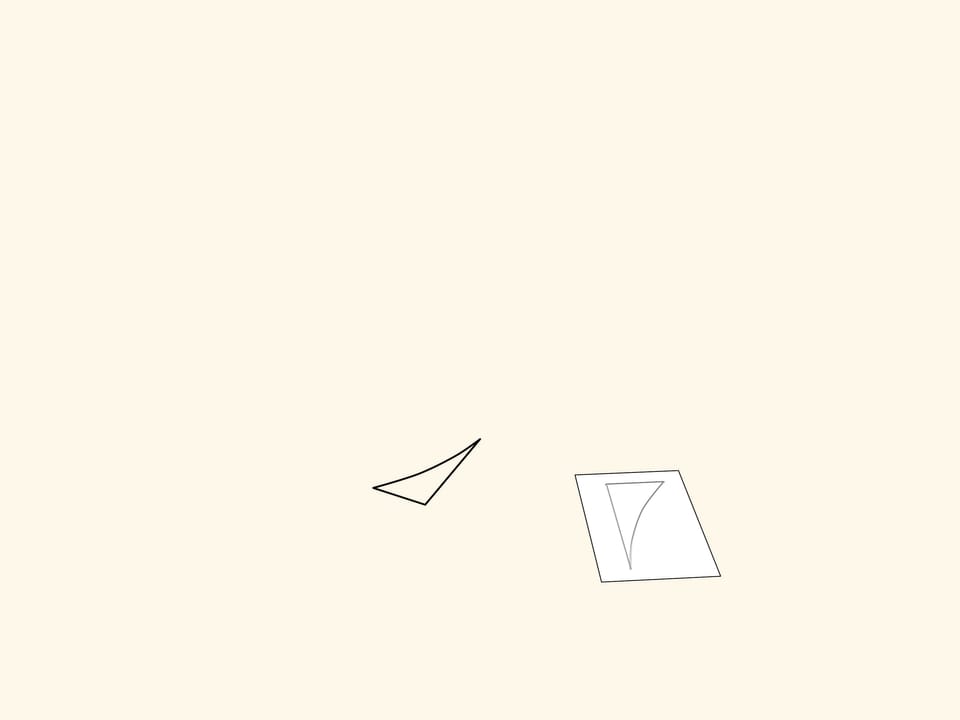
Prenons par exemple un triangle recourbé, et observons comment l’application de notre mécanisme va le transformer. Le résultat est une figure symétrique. Plus précisément, elle est égale à la figure initiale, mais est orientée différemment. Autrement dit, si le plan était une feuille de papier infinie avec la figure dessinée sur elle, alors nous devrions plier le papier le long de l’axe de symétrie, et calquer la figure de la moitié supérieure vers la moitié inférieure.
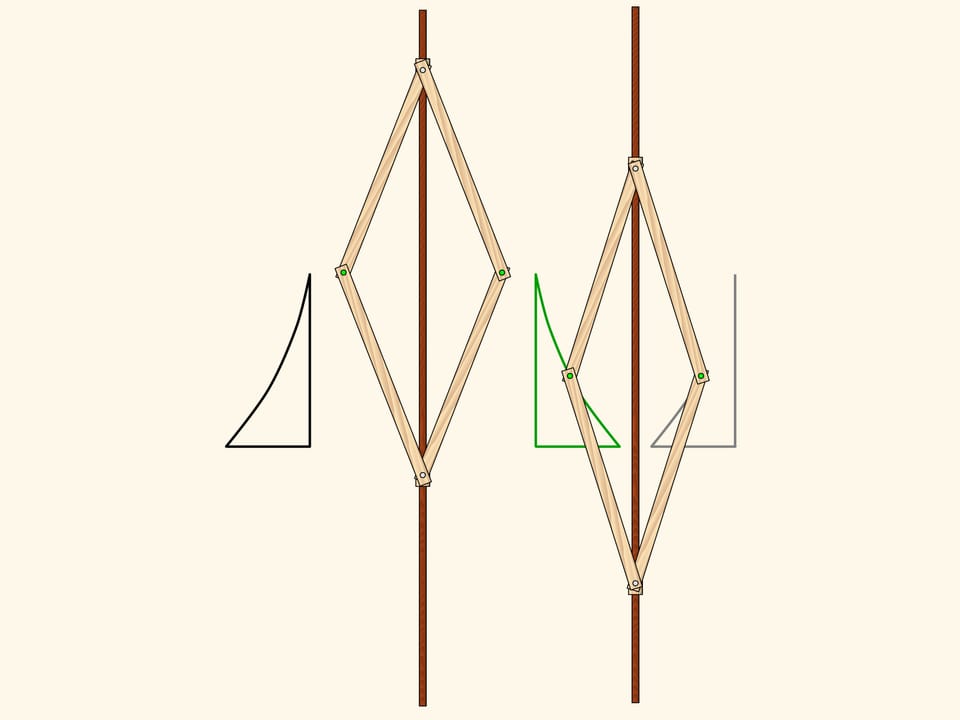
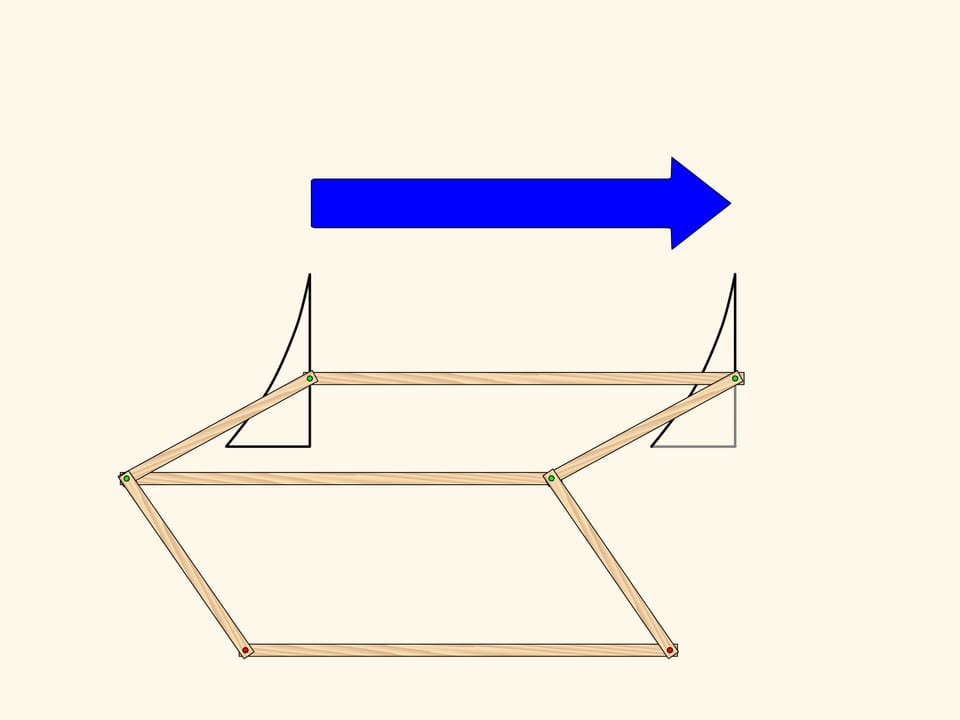
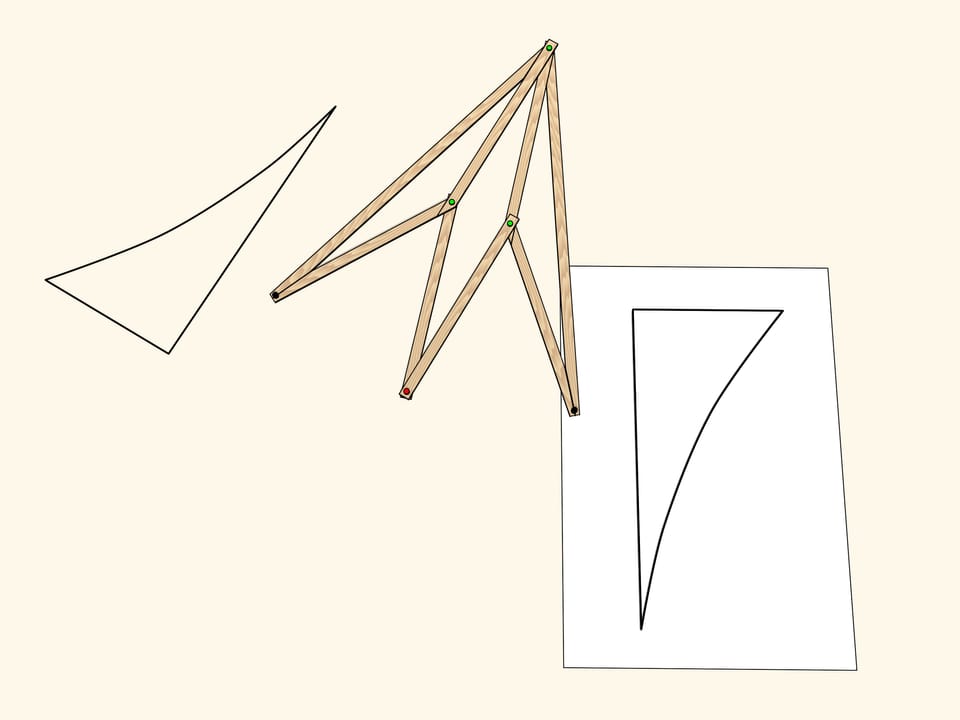
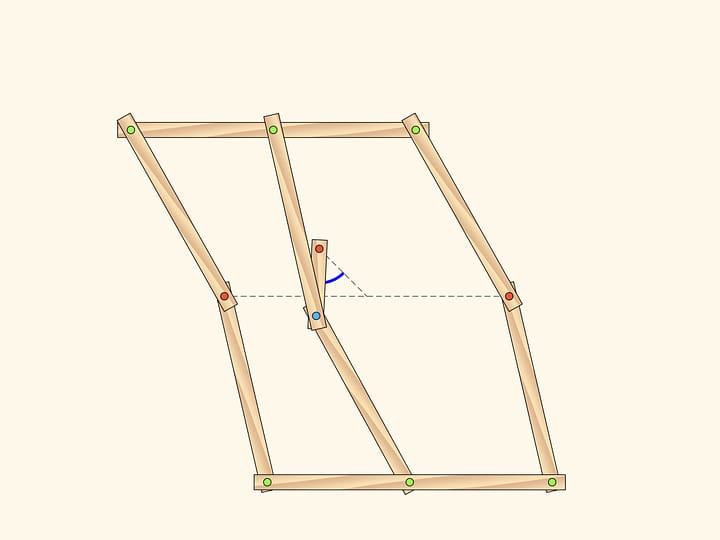
Appliquons maintenant au triangle obtenu par le mécanisme qui produit la réflexion, le même mécanisme, avec l’axe parallèle à celui que nous venons d’utiliser. Le triangle ainsi obtenu a la même symétrie du triangle initial, et l’on obtient du triangle initiale par transport parallèle, c’est–à–dire par translation. Un parallélogramme double, avec deux charnières fixes (en rouge) réalise cette application dans le plan. Ainsi, le résultat de deux réflexions d’axes parallèles est tout simplement une translation. Il est vrai aussi le réciproque, toute translation peut être décomposée en deux réflexions d’axes parallèles. Comme vous pouvez le voir, cette décomposition n’est pas unique.
En mathématiques le résultat d’applications successives est appelé composition; en termes de fonctions, on dit fonction composée. Ainsi, comme dans le langage de l’analyse, le résultat de la composition peut être réalisée soit en appliquant en séquence les actions correspondantes, soit en faisant leur composition et en l’appliquant comme un «produit». L’image–objet qui en résulte peut être assez différent de celui initial, auquel la composition a été appliquée.
Mais qu’est–ce qu’il arrive si les axes de symétrie ne sont pas parallèles?
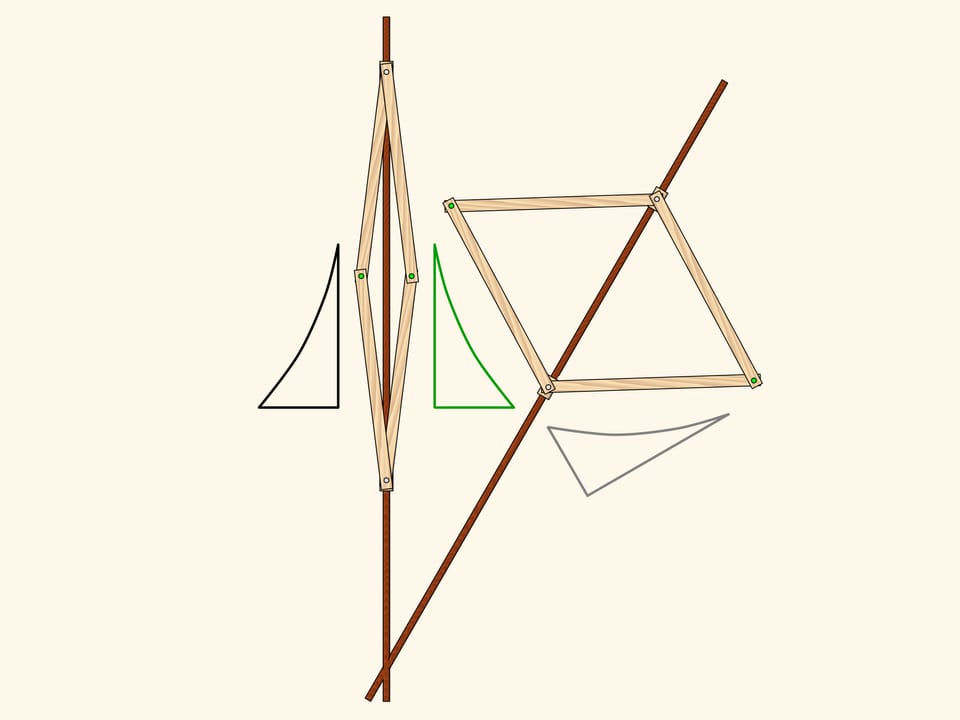
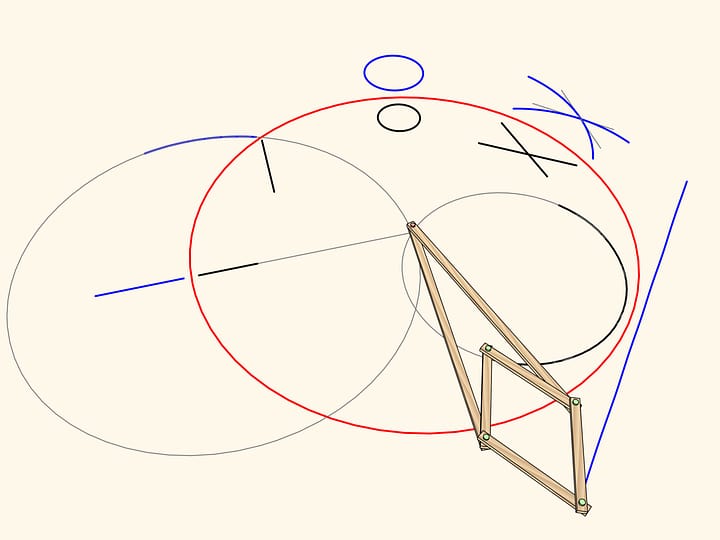
La composition de deux réflexions avec les axes non parallèles est une rotation avec le centre à l’intersection de deux axes. De plus, l’angle de cette rotation est égal au double de l’angle entre les axes. Comme dans le cas de la translation, toute rotation dans le plan peut être décomposée en deux réflexions.
Un mécanisme à charnières, basée sur le losange, réalise l’application de la rotation dans le plan.
Mais maintenant nous appliquons au plan (dans l’exemple de notre figure) dans la séquence une translation, puis une rotation. Est–ce qu’il est possible d’obtenir la figure résultante de la figure initiale par l’application d’un seul mouvement?
Décomposons la rotation en deux réflexions. De cette figure, il est évident que le processus d’obtention du triangle gri et successive réflexion peut être remplacé par une seule réflexion. Mais cette figure résulte alors de la composition de deux réflexions avec les axes non parallèles, que nous connaissons déjà, c’est–à–dire tout simplement une rotation.
Dessinons un triangle sur une table. Mettons au dessus une feuille de papier sur lequel suivrons la figure. Soulevons le papier et laissons le, de sorte qu’il tombe sans chavirer. De cette façon, nous obtenons, comme disent les mathématiciens, un déplacement “générique” plan, qui est une application qui préserve les distances et ne change pas l’orientation. Évidemment, il est possible que les figures initiale et finale diffèrent par une simple translation, mais les chances que la feuille se trouve dans une position si précise est extrêmement faible. Dans tous les autres cas il s’agit d’une simple rotation d’un certain angle par rapport à un certain centre.