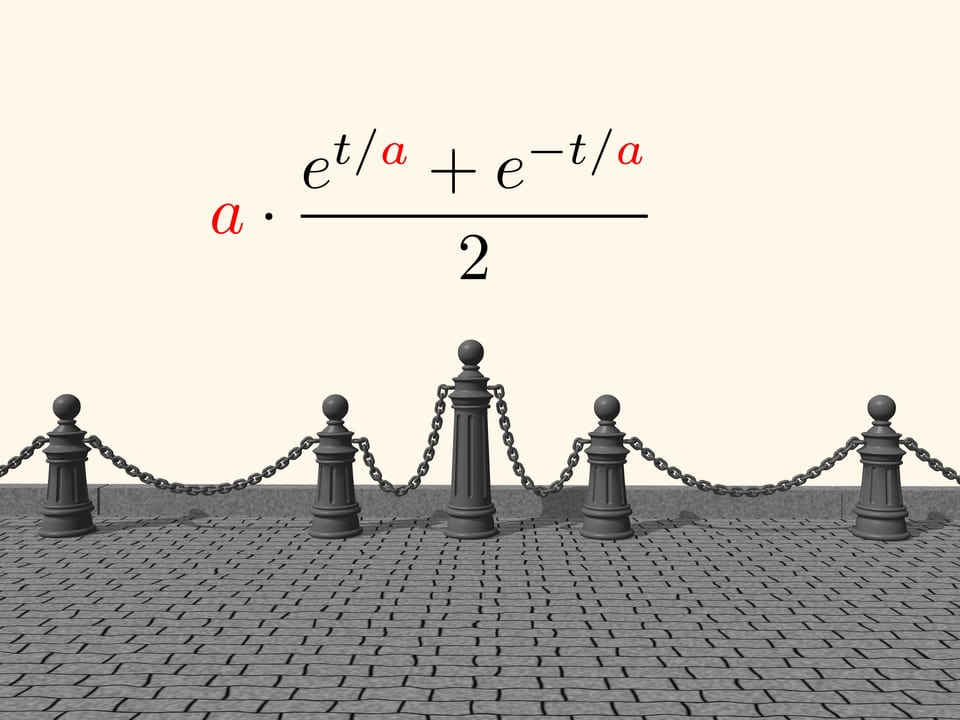... Un altro modo per tracciare su di una parete la parabola cercata è il seguente. Piantiamo nel muro due chiodi alla stessa altezza sull’orizzonte e a una distanza l’uno dall’altro che sia doppia della larghezza del rettangolo, in cui vogliamo iscrivere la parabola. Appendiamo ai chiodi le estremità di una catena sottile, di una lunghezza tale che il suo punto più basso si trovi a una distanza dal livello dei chiodi pari alla altezza del rettangolo. La catena, appesa, prende la forma della parabola, di modo che, segnando dei punti sul muro attraverso gli anelli della catena, otteniamo la traccia di una parabola, che è tagliata in due dalla linea perpendicolare al segmento tra i due chiodi che passa nel suo punto medio.
Galileo Galilei «Conversazioni e dimostrazioni matematiche.» 1638.
Ma lo scienziato si sbagliava. Tra la parabola e la linea tracciata dalla catena appesa c’è una piccola differenza. Appena mezzo secolo dopo Giovanni Bernoulli, Gottfried Leibniz e Christiaan Huygens trovarono l’equazione della «catenaria». In essa appare un parametro, cambiando il quale si possono ottenere diverse curve, corrispondenti a catene più o meno tese tra i due punti. Il nome «catenaria» lo dobbiamo proprio a Huygens.
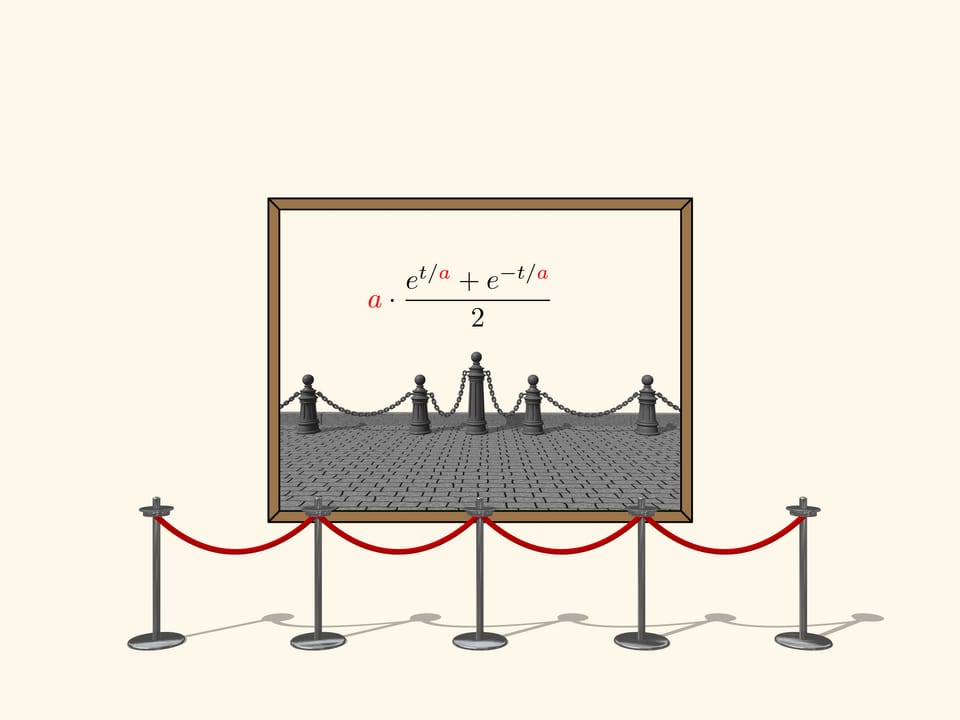
Lungo questa linea non corre soltanto una catena appesa, ma qualsiasi corda omogenea, sospesa tra due punti, soggetta alla forza di gravità. Questa linea la potreste osservare, per esempio, visitando un museo.
Ma capovolgiamo ora il nostro quadro.
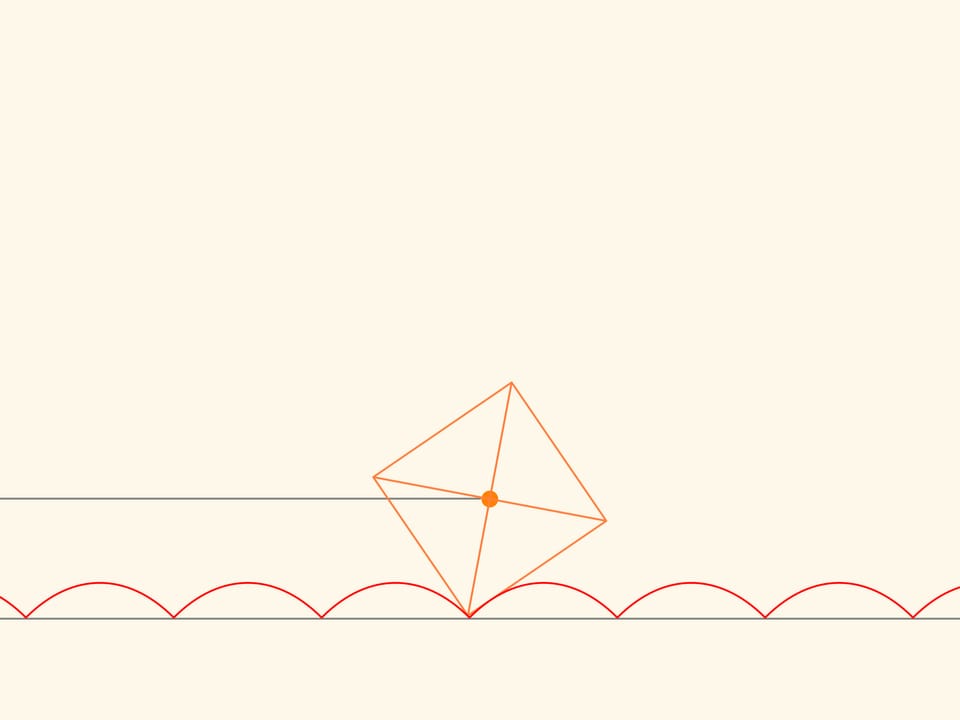
Se scegliamo il parametro dell’equazione in un dato modo, allora il centro di un quadrato, che ruota senza strisciare lungo l’arco di una catenaria, si muoverà in linea retta!
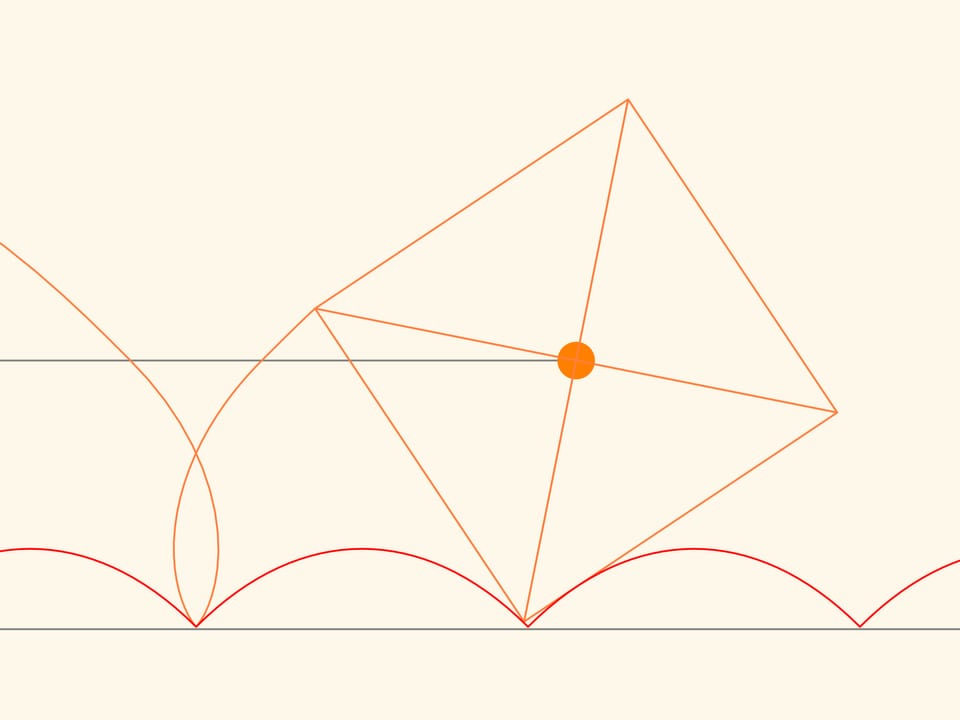
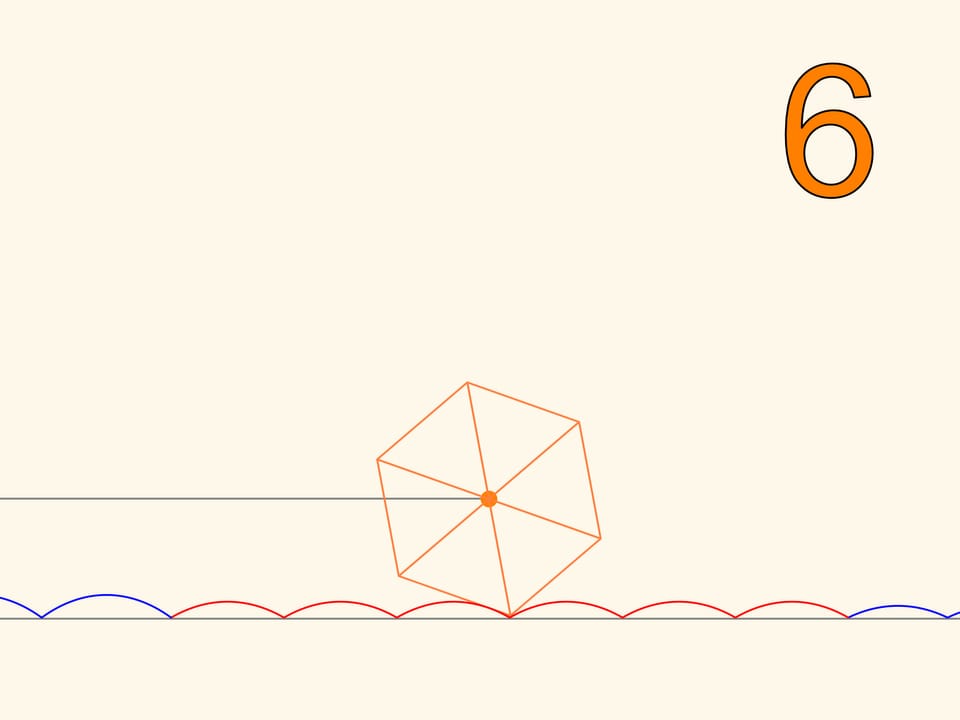
Tracciamo la traiettoria di uno dei vertici del quadrato. Questa curva non attraversa mai la catenaria e, quindi, un carrello che si muove su ruote quadrate si può fabbricare! Inoltre, la distanza tra gli assi del carrello non deve essere necessariamente un multiplo della lunghezza di una gobba della linea catenaria, poiché le ruote possono trovarsi in fasi di rotazione diverse.
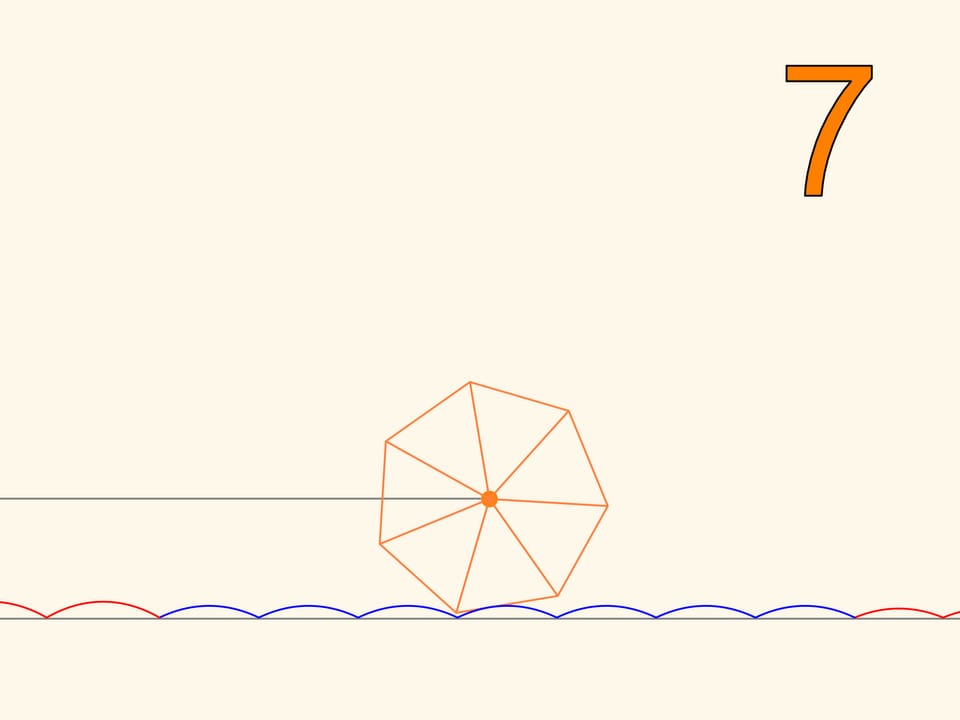
Abbiamo dunque imparato a spostarci su ruote quadrate. Ma scopriremo che si può andare anche su ruote che hanno la forma di qualsiasi poligono regolare. Solo che la strada non può essere piatta, ma dovrà avere la forma di una serie di catenarie, col valore del parametro scelto in base al numero dei lati del poligono. Quanto più il poligono regolare, aumentando il numero dei lati, si avvicina a un cerchio, tanto più il valore corrispondente del parametro diminuisce, e tanto più il tratto di strada, necessario per compiere un intero giro della ruota, si avvicina a un segmento della lunghezza della circonferenza. Г€ questa l’evoluzione della ruota, che, contrariamente ai poligoni regolari, che possono rotolare solo su catenarie, può rotolare su di un piano e cambiare direzione.
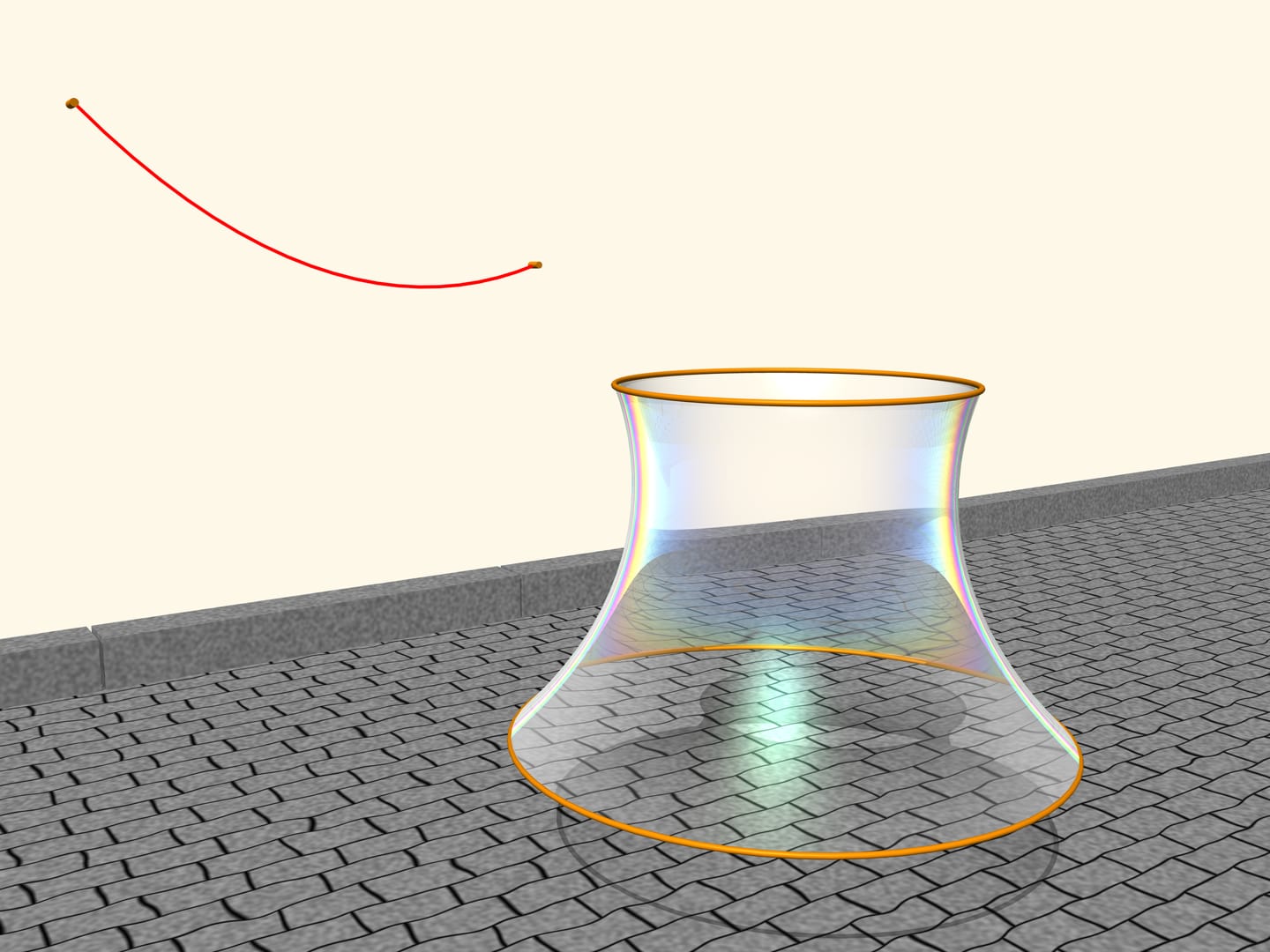
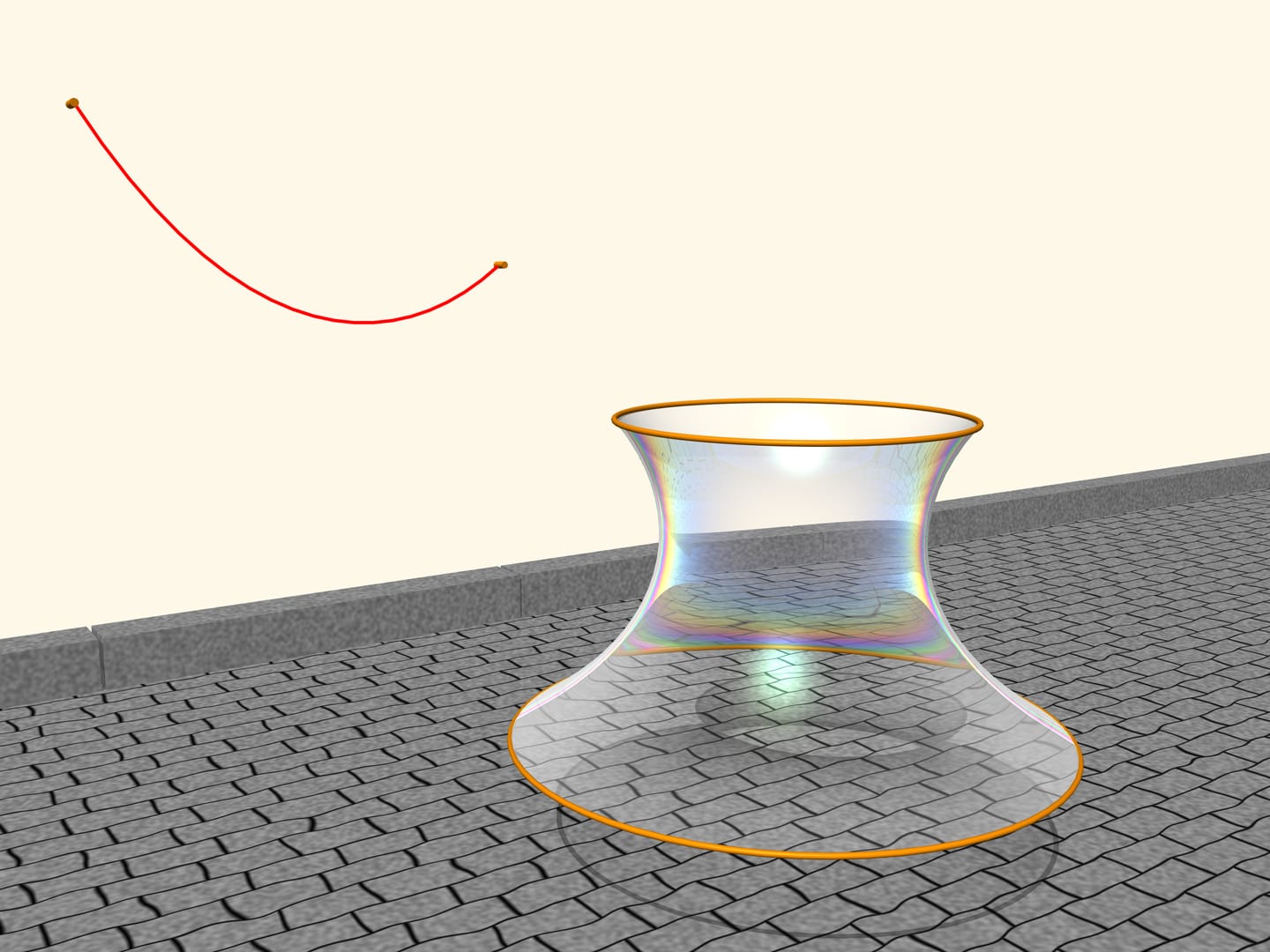
Osserviamo una pellicola di sapone tra due cerchi, posti su due piani paralleli. La pellicola di sapone è un oggetto straordinario: è estremamente leggera, sicché le forze interne sono notevolmente più forti della gravità, e per questo la pellicola prende sempre la forma di una superficie che ha l’area minima tra tutte le superfici con le stesse condizioni al contorno.
Quale forma prende la pellicola, sospesa tra i due cerchi? Viene fuori che prenderà la forma di una superficie, ottenuta dalla rotazione di una catenaria! Se si cambia la distanza tra i piani dove sono situati i cerchi, anche la superficie cambierà, ma il suo profilo sarà sempre quello di una catenaria di una lunghezza fissata, appesa a due paletti di altezza corrispondente posti alla corrispondente distanza. Tutto ciò fu dimostrato da Leonhard Euler nell’opera «Metodo per trovare linee curve con proprietà di massimo o di minimo» del 1744. Egli chiamò questa superficie catenoide (dal latino, catena, e dal greco éidos, aspetto).