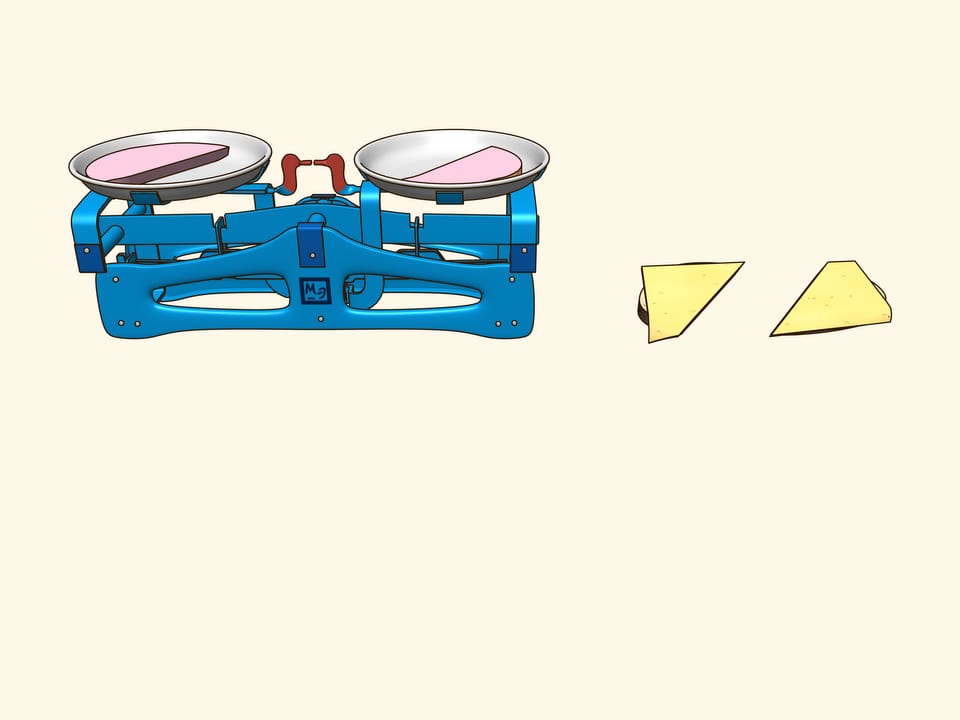
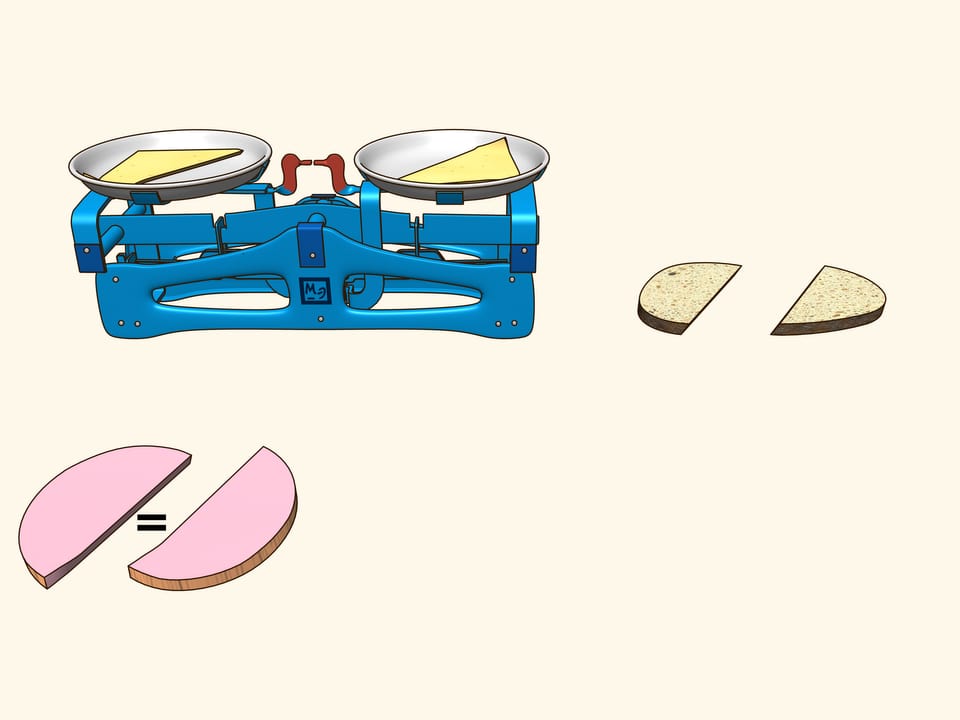
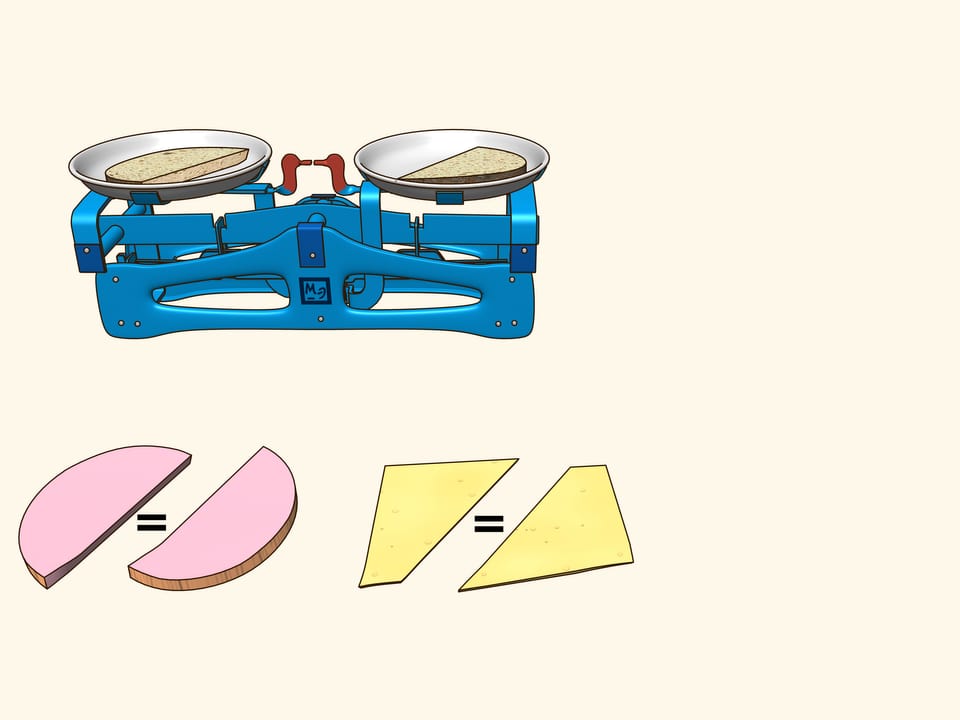
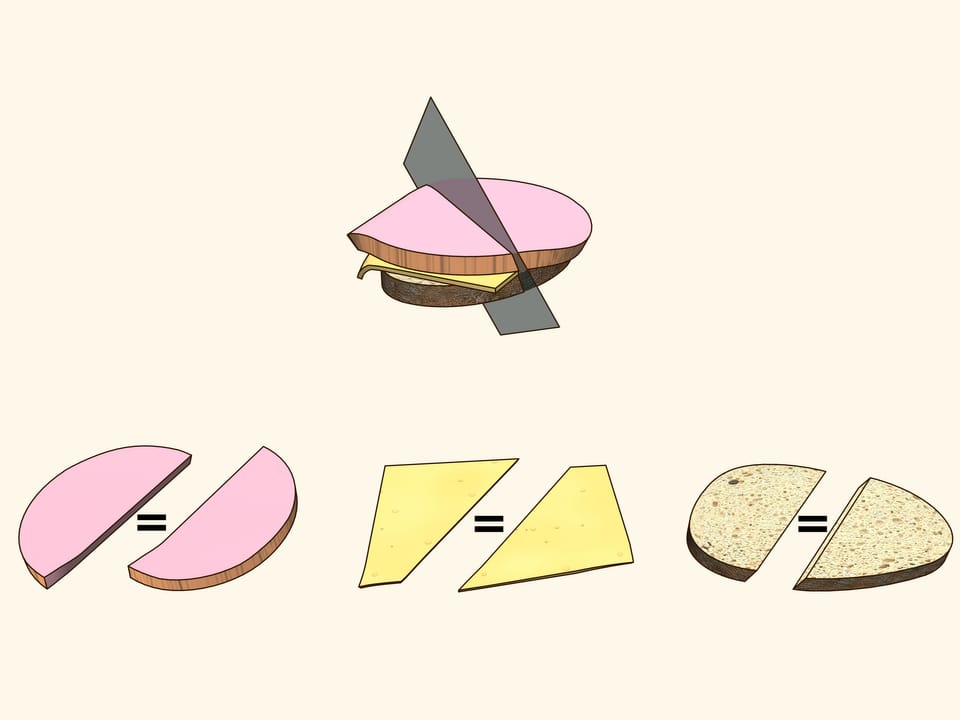Si può tagliare con un solo taglio un sandwich composto da una fetta di pane, una di formaggio e una di prosciutto in modo che le due parti contengano le stesse quantità di pane, formaggio e prosciutto? Mostreremo che è possibile…
Consideriamo prima di tutto il problema bi-dimensionale. Supponiamo che siano date nel piano due regioni qualsiasi. Esiste una retta che contemporaneamente taglia in due parti esattamente della stessa area sia la prima regione che la seconda?
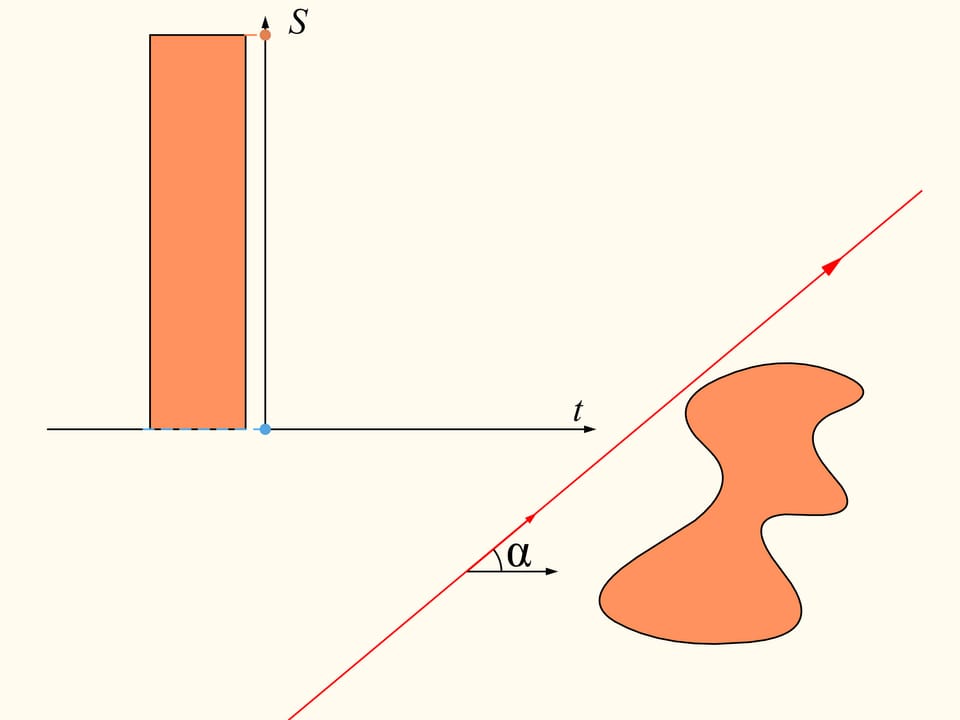
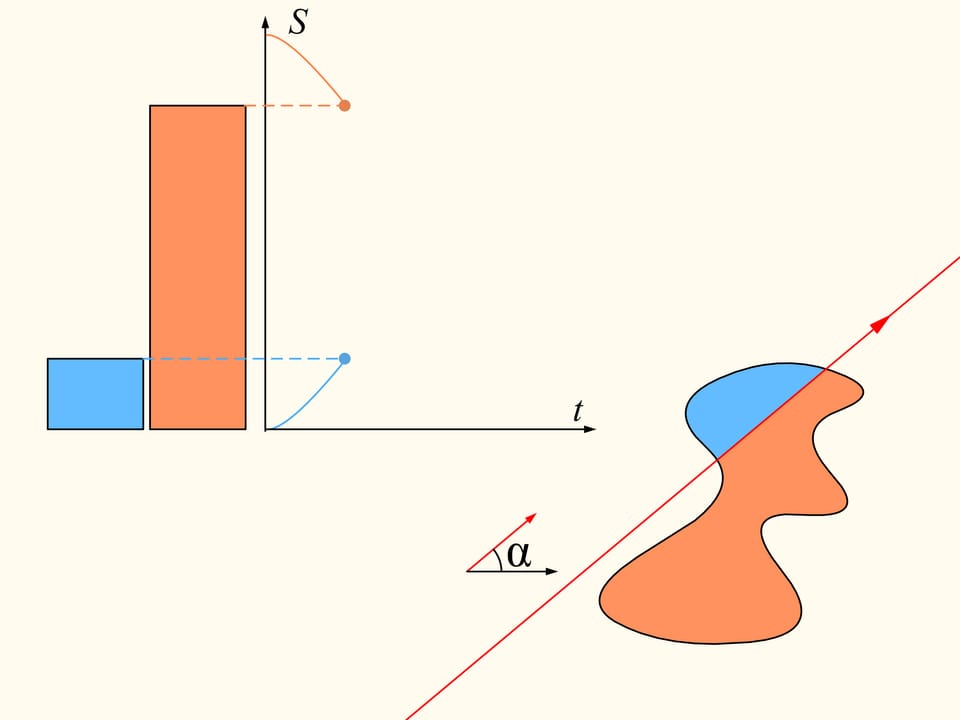
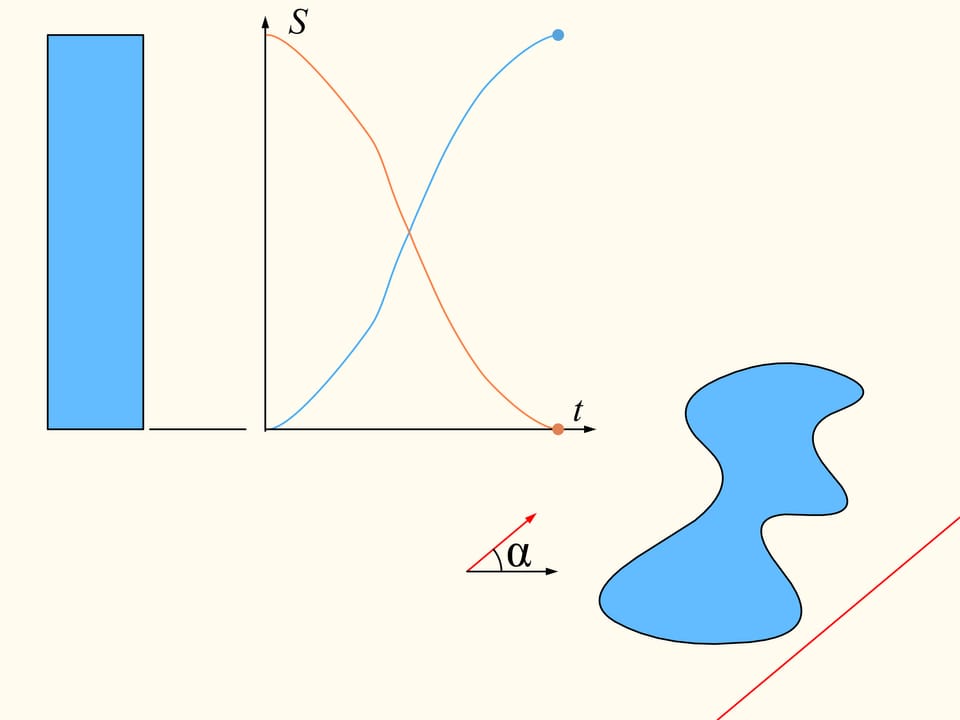
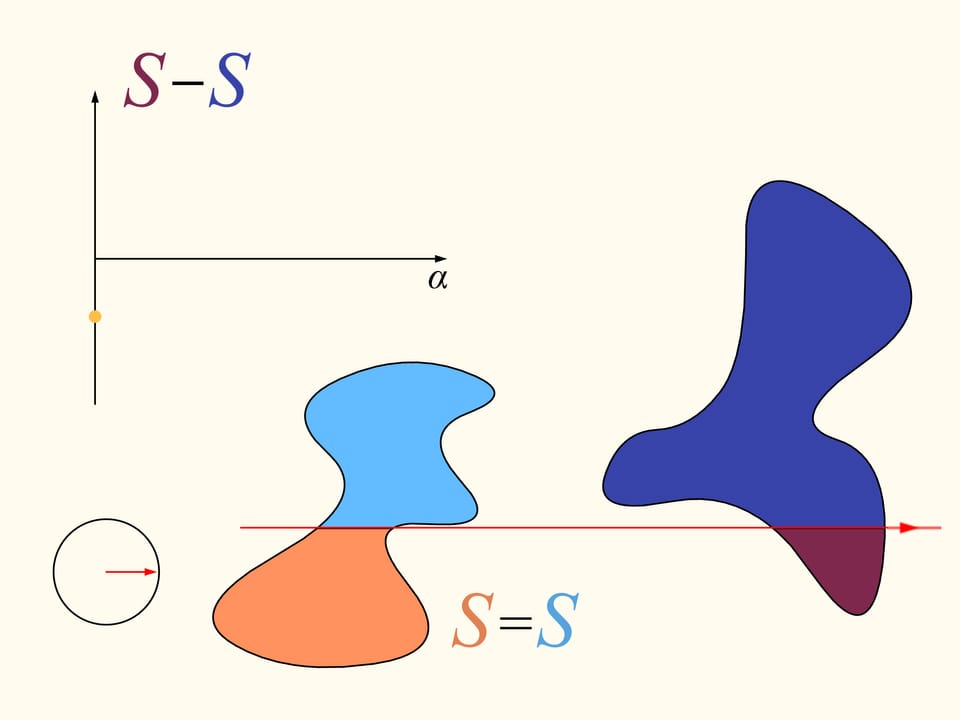
Per dimostrare che esiste, occupiamoci inizialmente di una sola delle regioni date. Scegliamo una direzione arbitraria. Esiste una retta avente questa direzione che divide la regione in due parti di uguale area? Dimostriamo che questa retta esiste qualsiasi direzione venga scelta. Prendiamo una retta così lontana che la regione sia completamente da una stessa parte rispetto ad essa. Costruiremo due grafici, rappresentanti le aree della regione che si trovano rispettivamente a destra e a sinistra della retta, in funzione della distanza di questa retta dalla sua posizione iniziale. All’inizio tutta la regione è a destra della retta, il che significa che l’elemento sinistro dell’istogramma è nullo e quello destro rappresenta tutta l’area della regione. Incominciamo a spostare la retta verso destra in modo che sia sempre parallela alla sua posizione iniziale. Durante questo spostamento l’area della regione che si trova alla sua destra diminuirà con continuità, mentre l’area alla sua sinistra aumenterà con continuità. Alla fine tutta la regione si troverà alla sinistra della retta. L’elemento sinistro dell’istogramma (in azzurro) rappresenterà allora l’area di tutta la regione mentre quello destro sarà nullo.
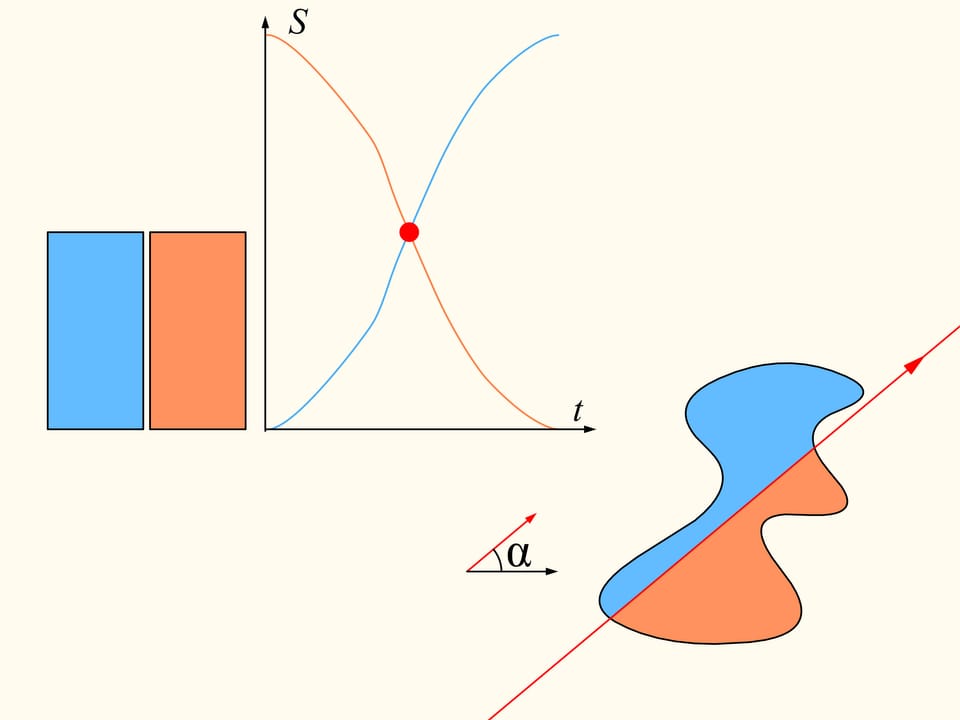
Se osserviamo i grafici rappresentanti le aree a destra e a sinistra della retta in funzione della distanza della retta dalla sua posizione iniziale, proprio a causa della loro continuità, esisterà da qualche parte un punto di intersezione. Questo punto dirà esattamente la posizione della retta che divide l’area della regione in due parti uguali.
Siccome la direzione della retta è stata scelta arbitrariamente, una retta che divide la regione in due parti uguali esiste in qualsiasi direzione.
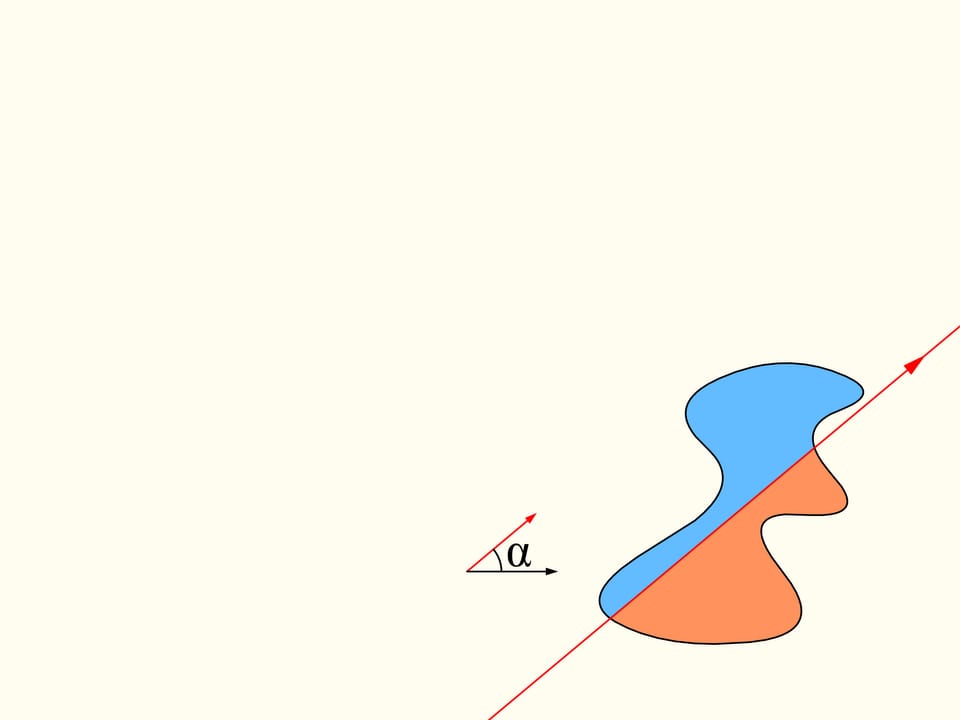
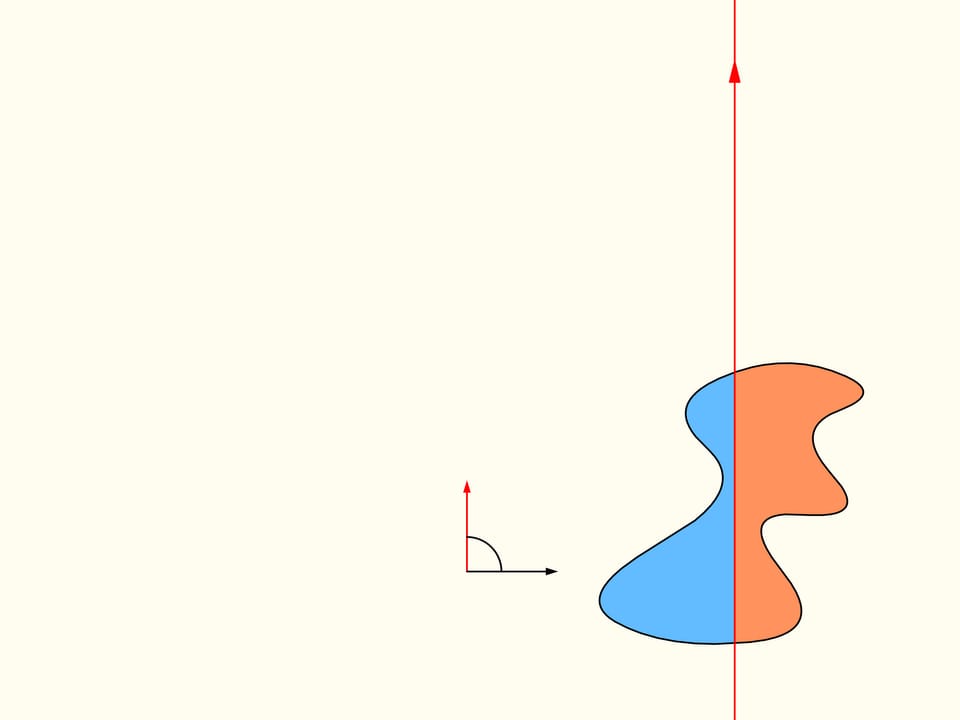
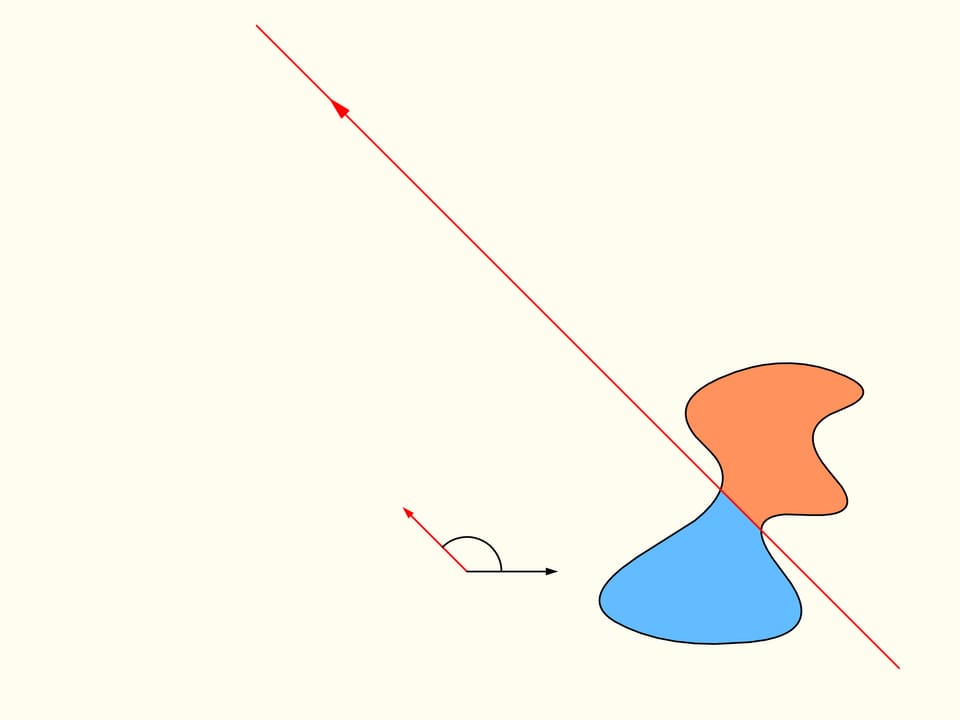
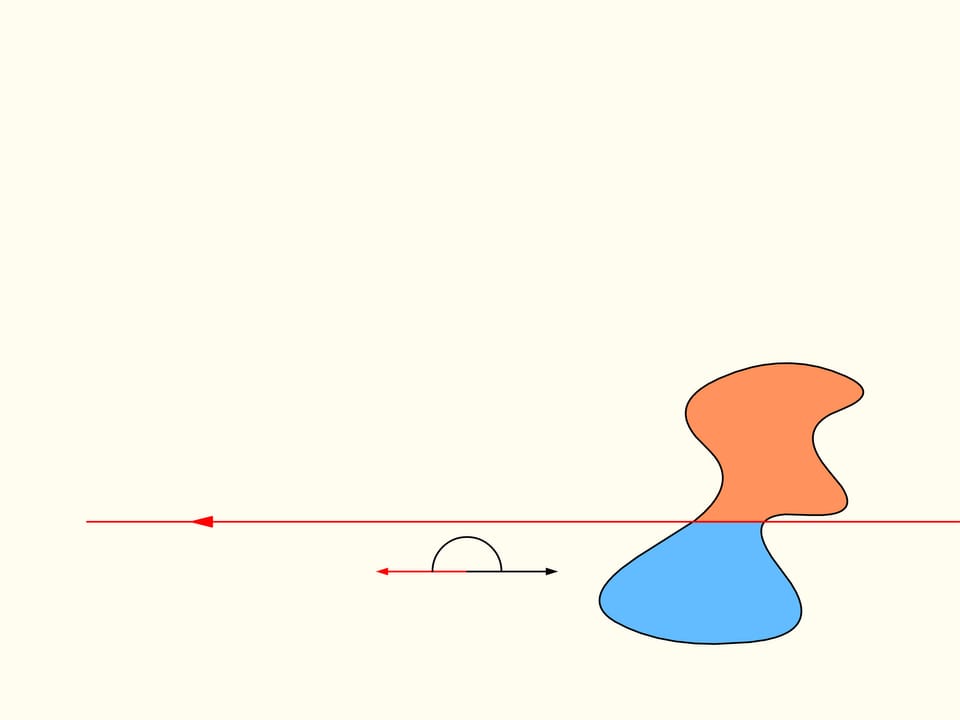
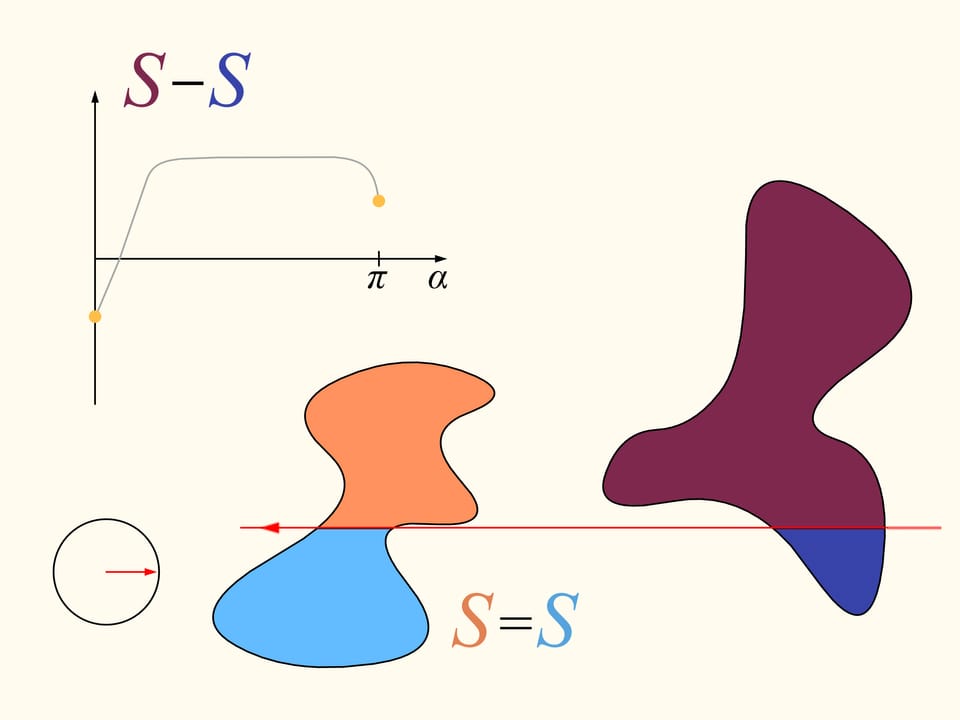
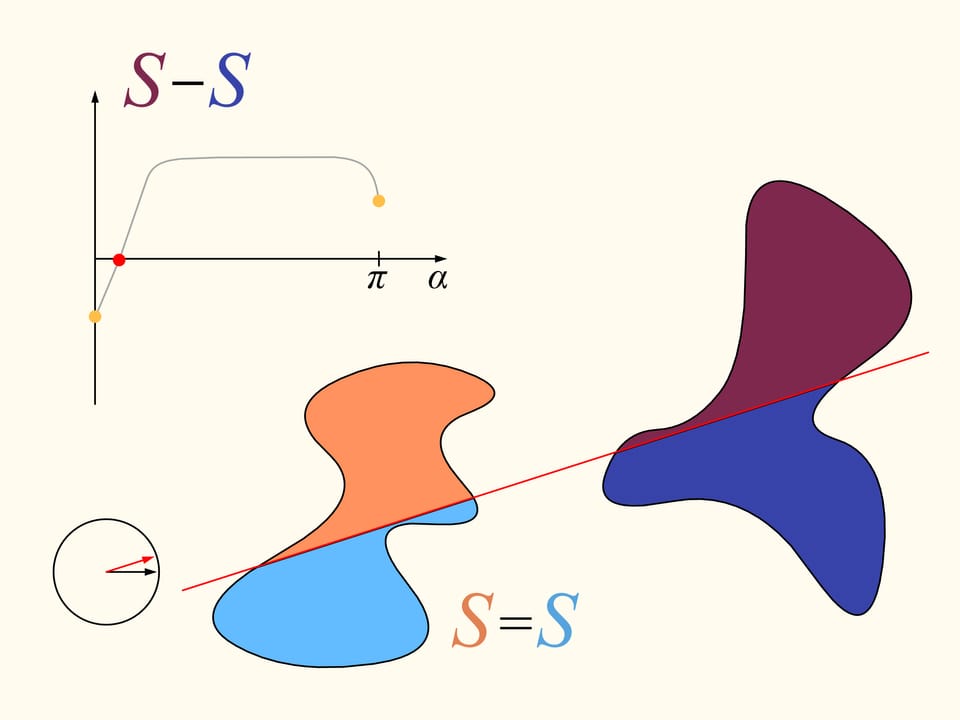
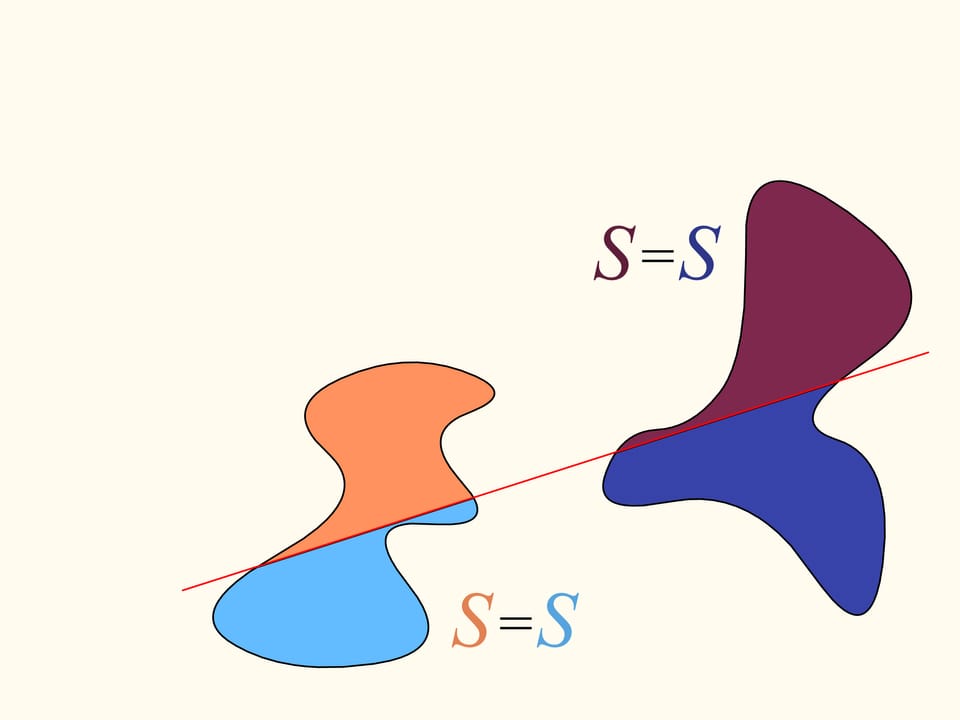
Torniamo al caso di due regioni. Considereremo solo quelle rette che tagliano la regione a sinistra in due parti uguali, e per iniziare scegliamo quella che è orizzontale e orientata verso destra. Essa taglierà la regione di destra in qualche modo. Ora cambiamo la direzione della retta, muovendoci nell’insieme delle rette che dividono in due la regione di sinistra. Costruiamo il grafico della differenza delle aree della regione di destra che si trovano a sinistra e a destra della retta, in funzione dell’angolo fatto dalla retta con quella iniziale, che è orizzontale. All’inizio questa differenza è negativa. Cambiando direzione con continuità la retta infine si troverà nella posizione iniziale, ma capovolta, ossia le aree a destra e a sinistra risultano scambiate tra loro. In questo istante il valore della differenza sarà positivo. Poiché la differenza cambia con continuità, il suo grafico, andando da un valore negativo a uno positivo deve incontrare la linea del valore nullo. A questo valore corrisponde un angolo che identifica la retta che divide esattamente in due la regione di destra. Abbiamo così trovato la retta cercata, che divide entrambe le regioni in due parti di uguale area.
Ecco come viene utilizzato il teorema di Bolzano-Cauchy. Purtroppo come tracciare questa linea in funzione delle forme delle regioni considerate, disposte arbitrariamente l’una rispetto all’altra, non lo possiamo sapere senza utilizzare altre idee e conoscenze. Ma essa esiste, per qualsiasi coppia di regioni! I teoremi di questo tipo si chiamano “ teoremi di esistenza”.
Passiamo ora al caso tridimensionale. Al posto di due regioni nel piano bi-dimensionale consideriamo tre oggetti arbitrari, disposti arbitrariamente uno rispetto all’altro. Al posto delle aree, considereremo i volumi, e al posto della retta, un piano. Avviene che anche in questo caso con un ragionamento simile a quello usato nel piano, possiamo dimostrare un teorema di esistenza. Per tre oggetti qualsiasi esiste un piano che divide ciascuno di essi in due parti di uguale volume.
Perché la vita abbia più sapore, consideriamo un sandwich fatto di pane, formaggio e prosciutto. Si tratta di tre oggetti, disposti in qualche modo uno rispetto all’altro. Cercate di dimostrare che esiste un piano che taglia il prosciutto in parti uguali e contemporaneamente taglia anche il formaggio e il pane in parti uguali. Utilizzando ragionamenti supplementari, questo piano è stato trovato per il sandwich mostrato nel film, ed effettivamente è evidente dalla verifica che tutti e tre gli oggetti sono stati divisi in due parti uguali!