In seguito all’invenzione della macchina a vapore di James Watt si pose il problema di costruire un meccanismo a cerniere, che trasformasse il moto circolare di una cerniera nello spostamento di un’altra cerniera in linea retta.
Per lungo tempo sia scienziati sia ingegneri cercarono di risolvere questo problema, ma non vi riuscirono. Costruirono solo dei meccanismi capaci di far muovere una cerniera in modo quasi rettilineo, ma non perfettamente. Venne in loro aiuto, infine, una bella teoria matematica…
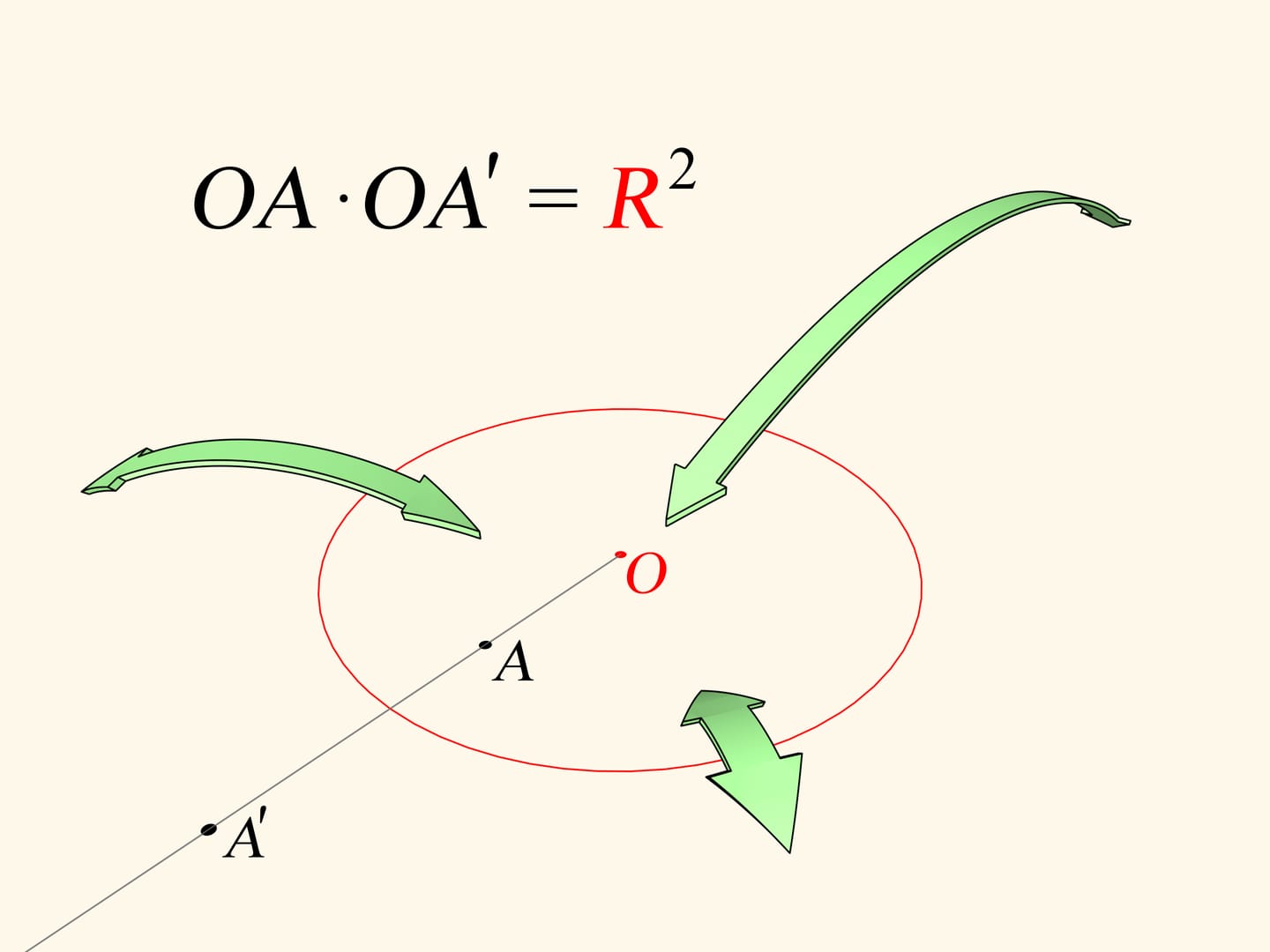
Ricordiamo che nel piano l’inversione rispetto a un cerchio è un’applicazione biunivoca dell’interno del cerchio (escluso un punto, il centro) nel resto del piano all’esterno del cerchio. L’immagine del punto $A$ è un punto $A’$, che sta nel raggio uscente dal centro del cerchio e passa attraverso il punto $A$. La posizione sul raggio è definita dall’uguaglianza $OA \cdot OA'=R^2$, dove $O$ è il centro del cerchio, e $R$ è la lunghezza del suo raggio. Con l’aiuto dell’inversione si risolvono molti problemi di geometria. Come vedremo, questa applicazione permette di risolvere non solo dei problemi teorici.
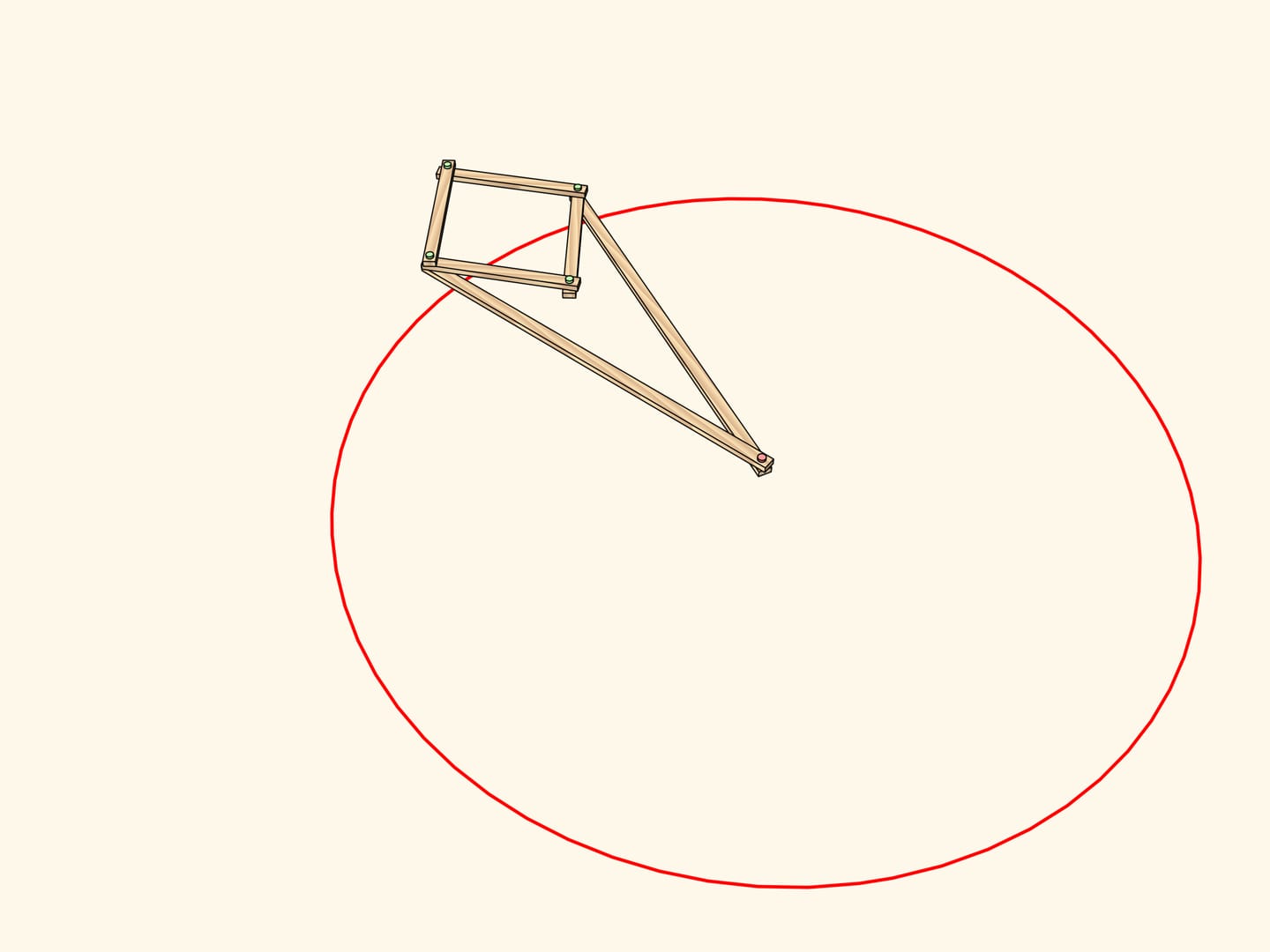
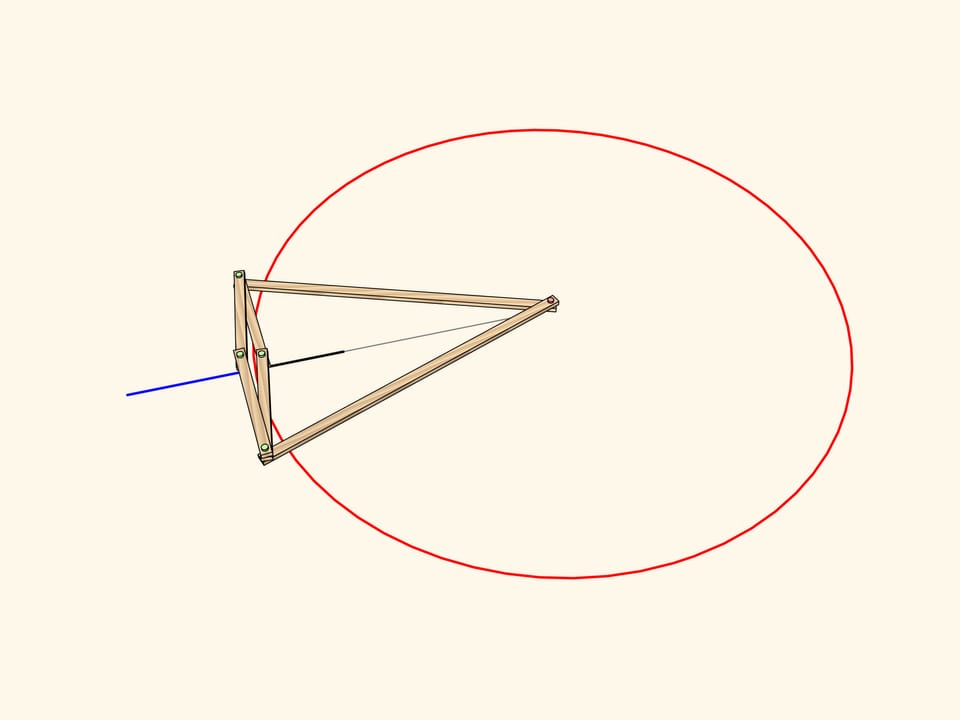
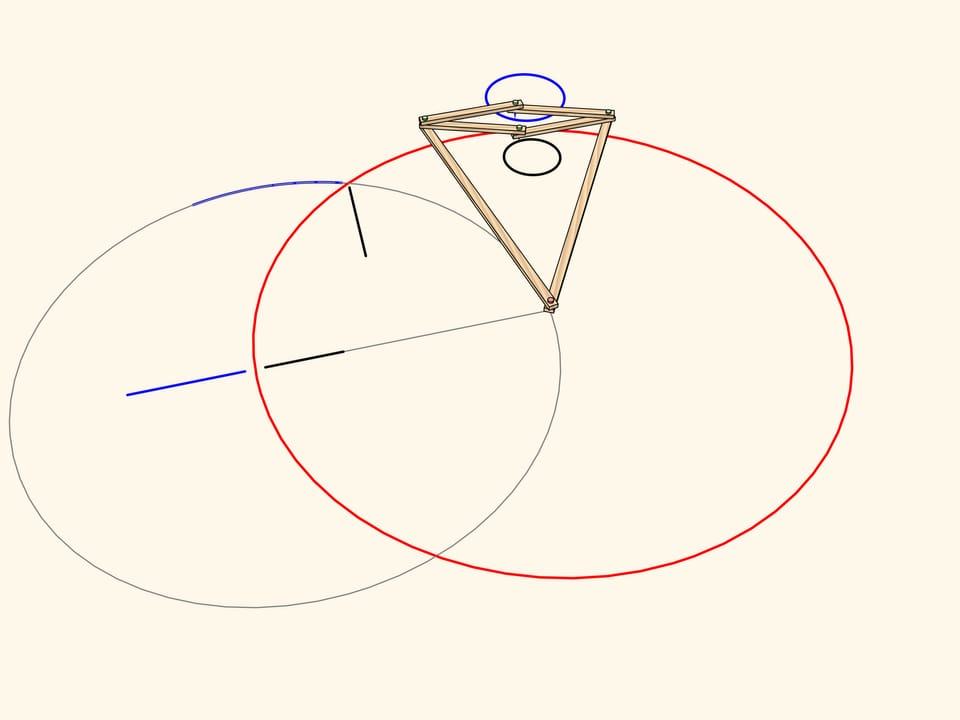
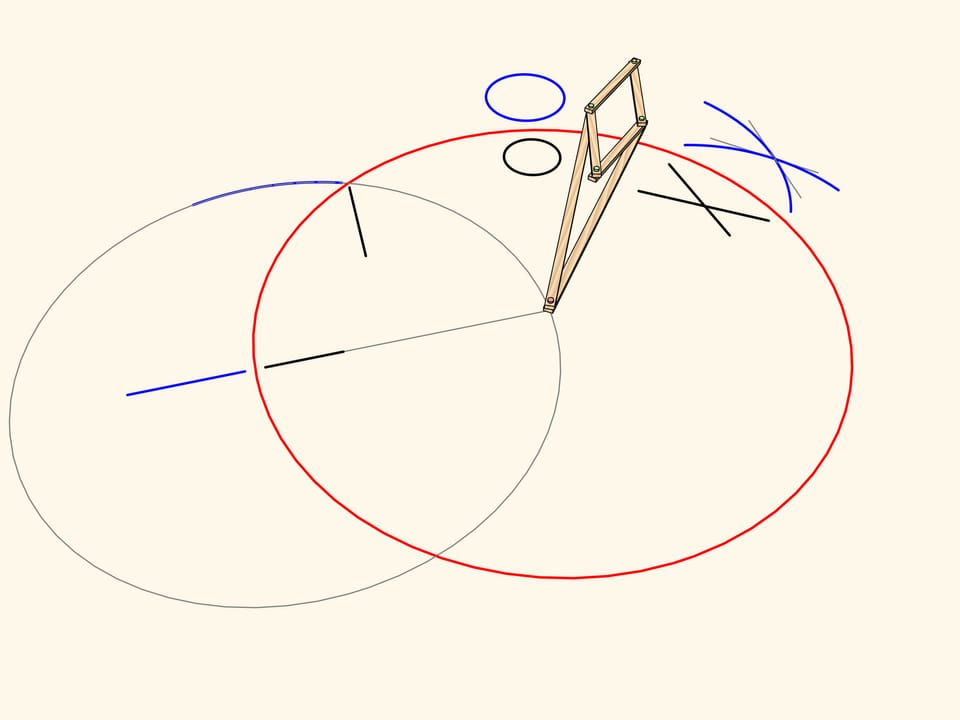
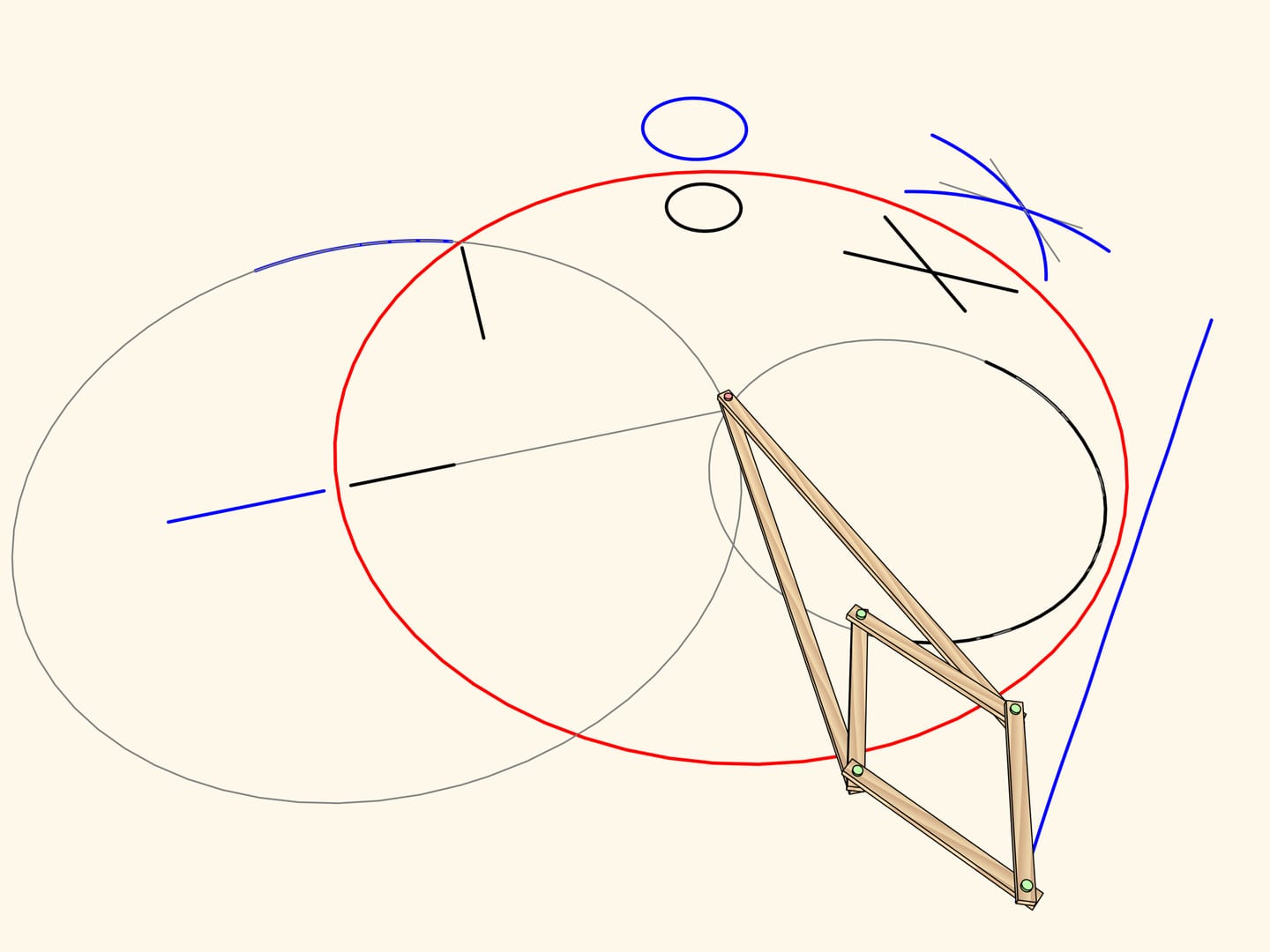
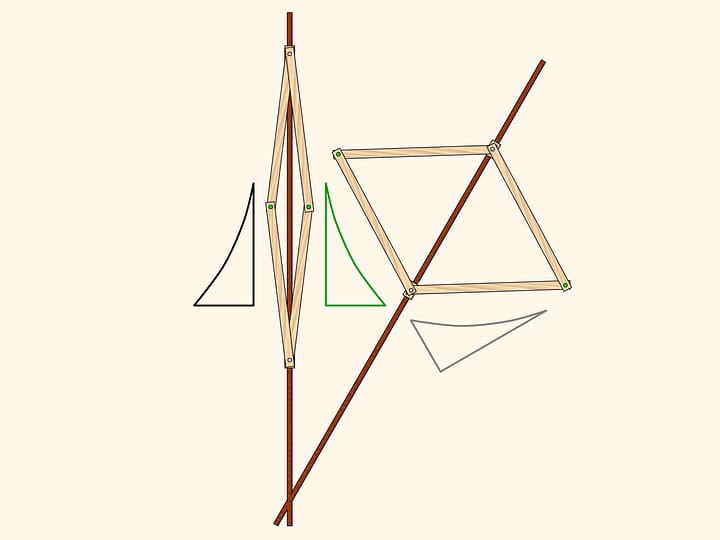
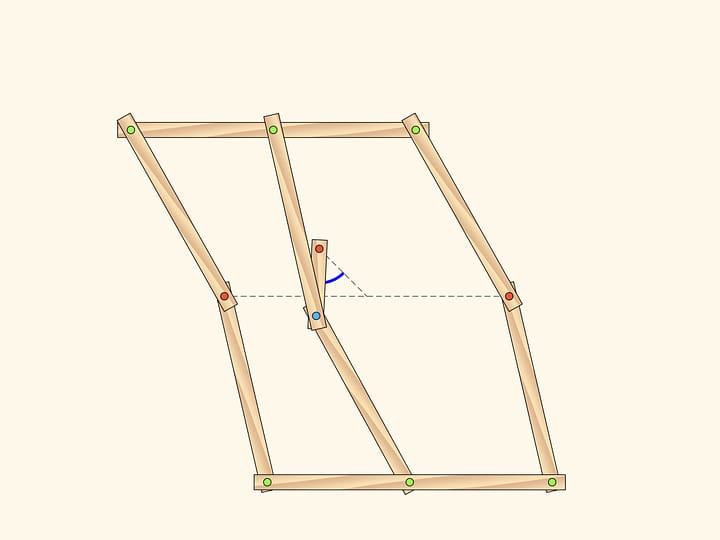
Consideriamo un meccanismo con una cerniera applicata a un punto fisso (marcato in rosso). Due lunghe barre della stessa lunghezza sono applicate ad una estremità a questa cerniera, mentre alle altre estremità sono applicate le due cerniere opposte di un rombo, fatto di quattro barre più corte unite da quattro cerniere.
Questo meccanismo realizza l’inversione rispetto al cerchio col centro nel perno fisso e con un raggio che dipende dalle lunghezze degli elementi del meccanismo. La curva tracciata da una delle due cerniere libere del rombo risulta essere l’immagine, per inversione, della curva tracciata da quell’altra.
Con l’aiuto del nostro meccanismo osserviamo ora che proprietà ha l’applicazione di inversione.
Dalla stessa definizione dell’inversione è evidente che l’immagine di un segmento, che sta su una retta passante per il centro del cerchio, è un segmento che sta ancora su quella stessa retta.
L’immagine di un segmento, che sta su di una retta che non passa per il centro dell’inversione, è un arco di cerchio, che passa per il centro dell’inversione.
Un cerchio, che non passa per il centro e che non interseca il cerchio dell’inversione, viene trasformato dall’inversione in un altro cerchio.
L’inversione conserva gli angoli tra due curve, però ne inverte le orientazioni. Queste applicazioni in matematica vengono dette “anticonformi” (Sono conformi quelle che conservano sia gli angoli, sia le orientazioni).
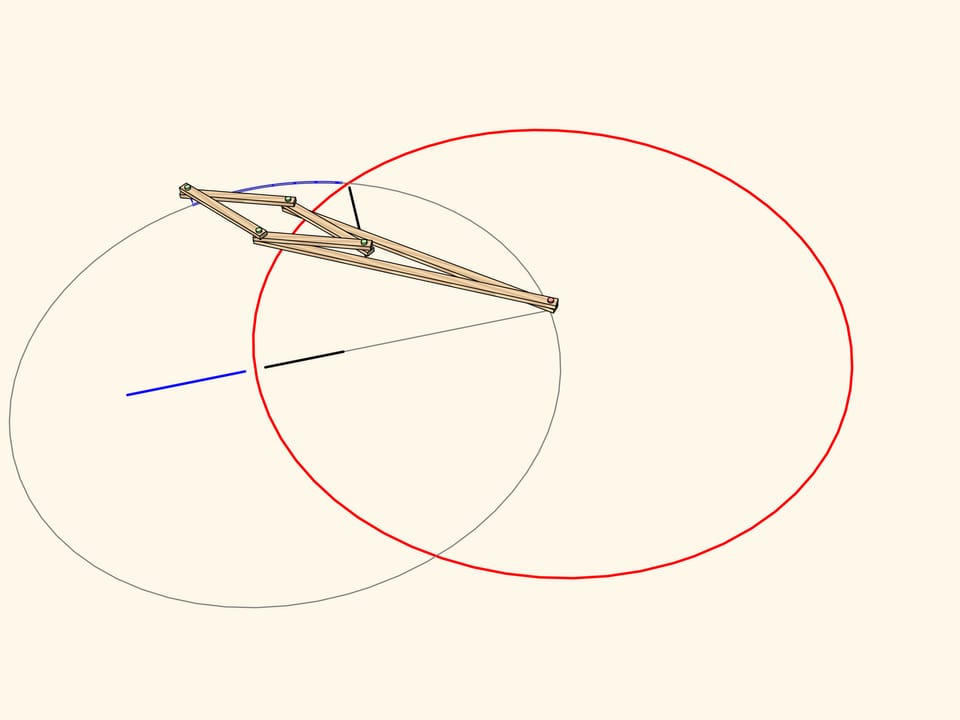
Un arco di cerchio, passante per il centro dell’inversione, viene trasformato… esattamente in un segmento di retta!
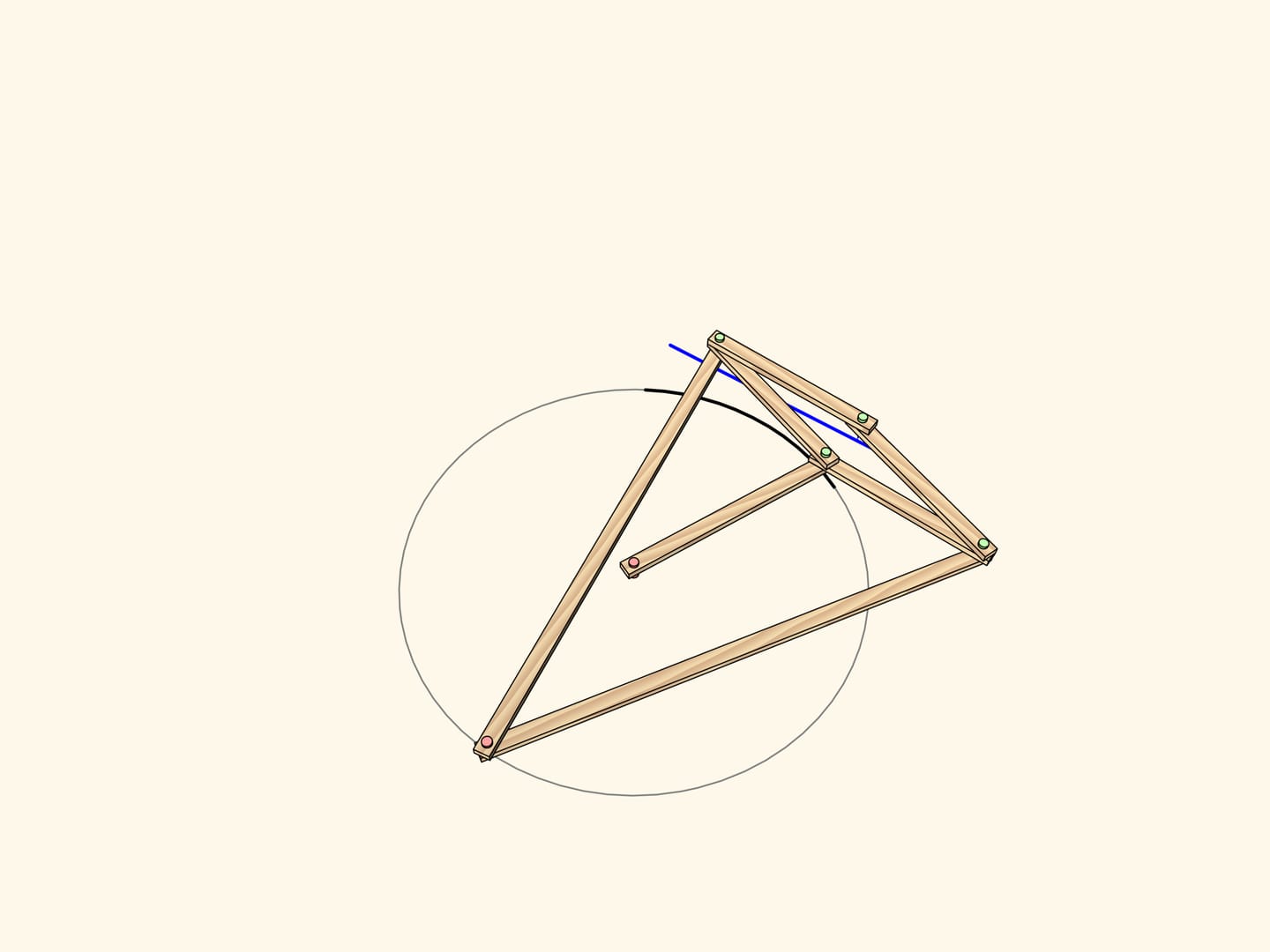
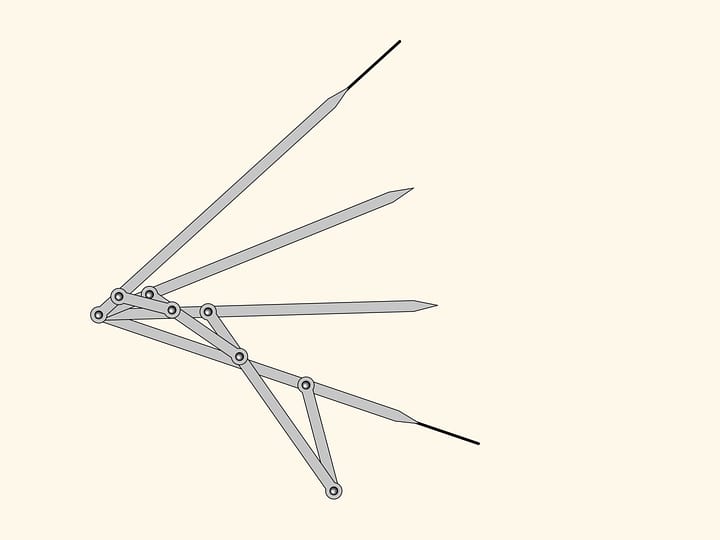
È proprio questa proprietà che fu usata nella costruzione del primo meccanismo della storia capace di tracciare segmenti rettilinei. Affinché una cerniera del rombo tracci esattamente un cerchio passante per il centro del cerchio dell’inversione, aggiungiamo una cerniera fissa nel centro del cerchio passante nel centro dell’inversione, e un elemento lungo quanto il suo raggio, fissato a questa cerniera e a una cerniera del rombo. L’altra cerniera libera traccerà sempre un segmento di linea retta. A causa del fatto che viene utilizzata la proprietà dell’inversione, questi meccanismi vengono spesso chiamati inversori.
Peaucellier (Charles Nicolas Peaucellier, 1823—1913) informò gli ufficiali del corpo degli ingegneri dell'esercito della costruzione di un inversore nel 1864 in una lettera privata. Egli tuttavia non fornì alcun dettaglio sulla costruzione del meccanismo. Nel 1868 Lipman Lipkin (1846—1876), studente di Chebyshev, inventò l’inversore. Il suo articolo dettagliato fu pubblicato nel 1870, e solo nel 1873 apparve l’articolo di Peaucellier con la descrizione di quello stesso meccanismo e con riferimento al lavoro di Lipkin.
In seguito furono inventati altri meccanismi per tracciare rette, basati su altre idee matematiche. Ma l’inversore si distingue per la sua bellezza e le sue buone proprietà meccaniche per le quali ha trovato molte applicazioni in ingegneria.