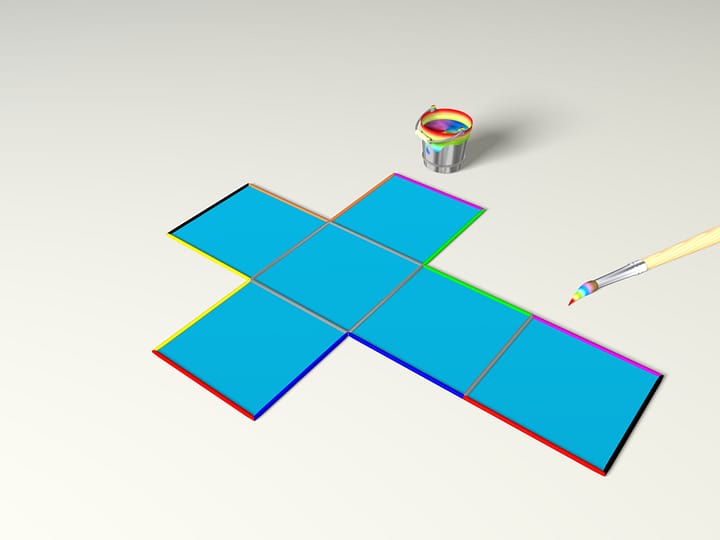
Gli sviluppi dei poliedri a noi più familiari non sono di un solo tipo. Ma non vorreste da questo pezzo di cartone ottenere un tetraedro regolare?
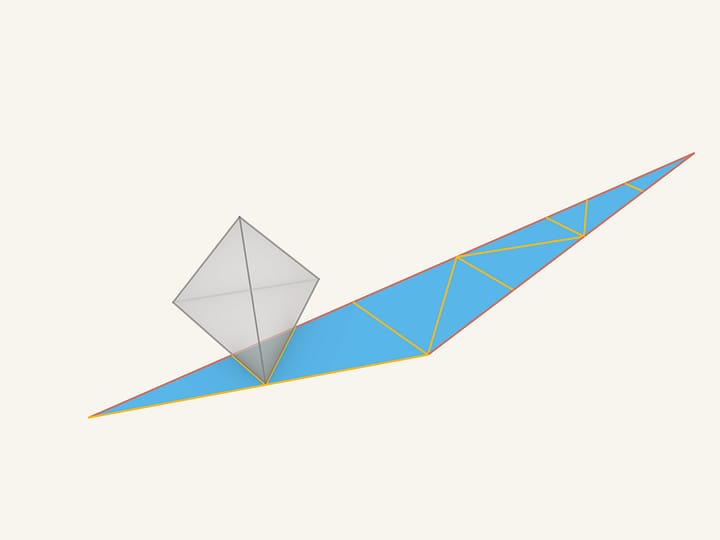
Prendiamo lo sviluppo più comune del tetraedro.
Tracciamo un segmento dall’angolo del grande triangolo sino al punto medio del lato opposto, (che è un vertice del tetraedro iniziale) e tagliamo il nostro pezzo di cartone lungo di esso. Ruotiamo un pezzo dello sviluppo intorno al punto corrispondente al vertice del tetraedro. Dopodiché incolliamo i due spigoli. Osservate che nel tetraedro iniziale questi spigoli erano già attaccati, perciò le condizioni di incollamento dei bordi del nostro sviluppo sono rispettate. Ma ora abbiamo in più un pezzo di bordo, che non esisteva nello sviluppo iniziale. Coloriamo di rosso questo “falso spigolo”.
Ripetiamo l’operazione ancora una volta.
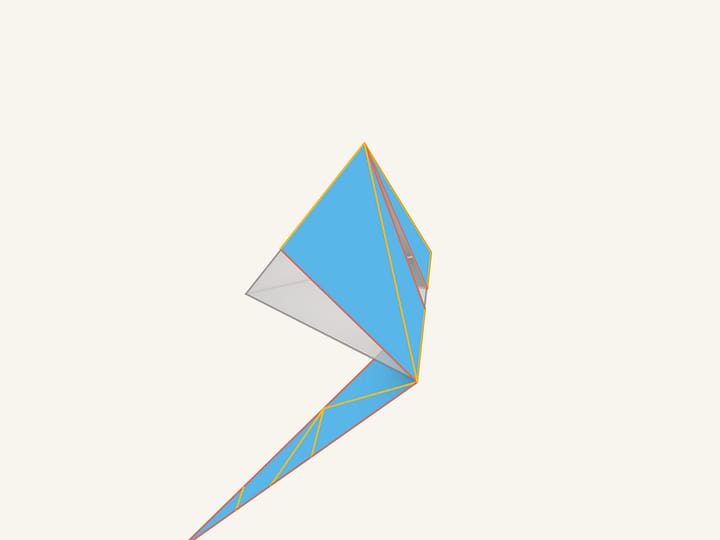
Tracciamo di nuovo un segmento dall’angolo al punto medio del lato opposto e tagliamo il cartone lungo di esso. Facciamo ruotare e incolliamo. Otteniamo quello stesso pezzo di cartone che si è visto all’inizio del film!
Vedremo ora che il pezzo di cartone appena ottenuto è lo sviluppo del poliedro iniziale. Nella parte sinistra del triangolo ci sono dei pezzi che non abbiamo spostato durante tutte le operazioni. Uno dei piccoli triangoli corrisponde a una parte della base del tetraedro iniziale.
Partendo da questo ripieghiamo la nostra figura fino ad ottenere il tetraedro. Come potete vedere, tutti i pezzi combaciano!
Ognuno dei segmenti rossi, i “falsi spigoli”, separa due triangoli che giacciono su uno stesso piano, il che significa che dopo l’incollamento questi spigoli si possono eliminare. Gli altri segmenti, invece, che erano stati colorati di giallo, si trovano sugli spigoli del tetraedro e sono dei veri spigoli.
Ma alla questione, se si può ottenere un poliedro convesso da un dato pezzo di cartone, risponde un teorema del grande geomètra russo Aleksander Danilovich Aleksandrov. Dove saranno i vertici di questo poliedro, si può facilmente capire. Ma come tracciare i veri spigoli tra questi vertici, finora i matematici non lo sanno in generale definire. Ma questa è già un’altra storia, per un successivo Studio…