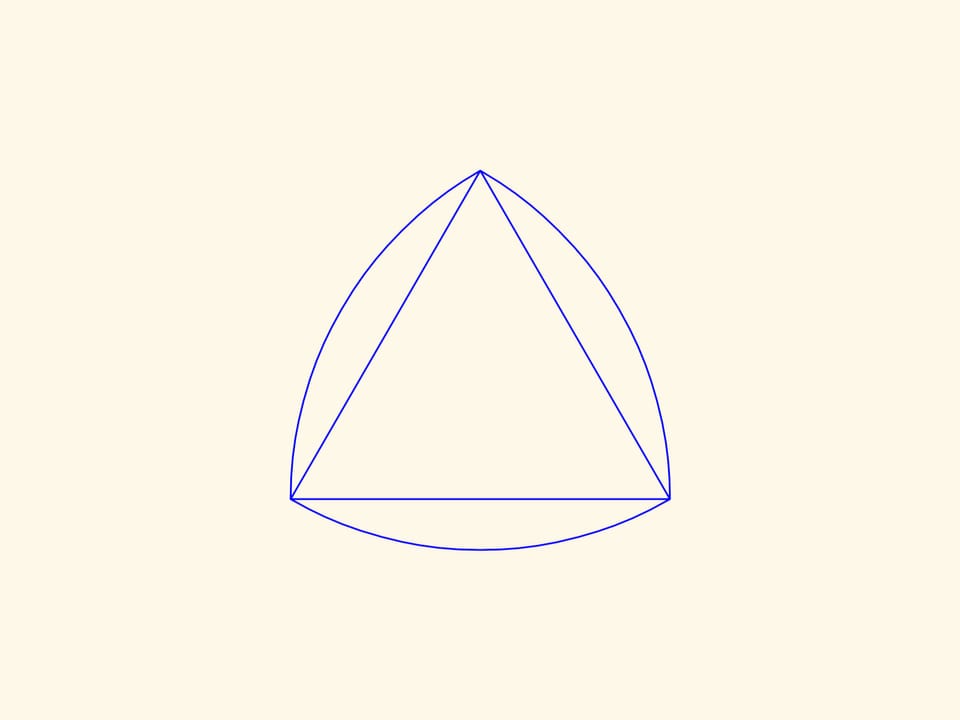
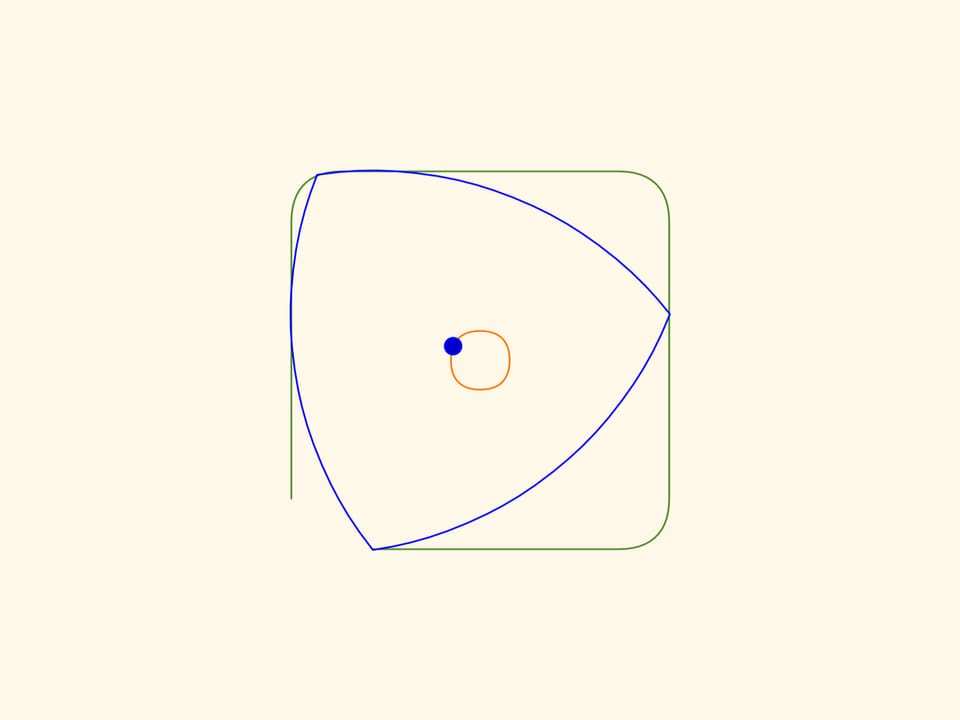
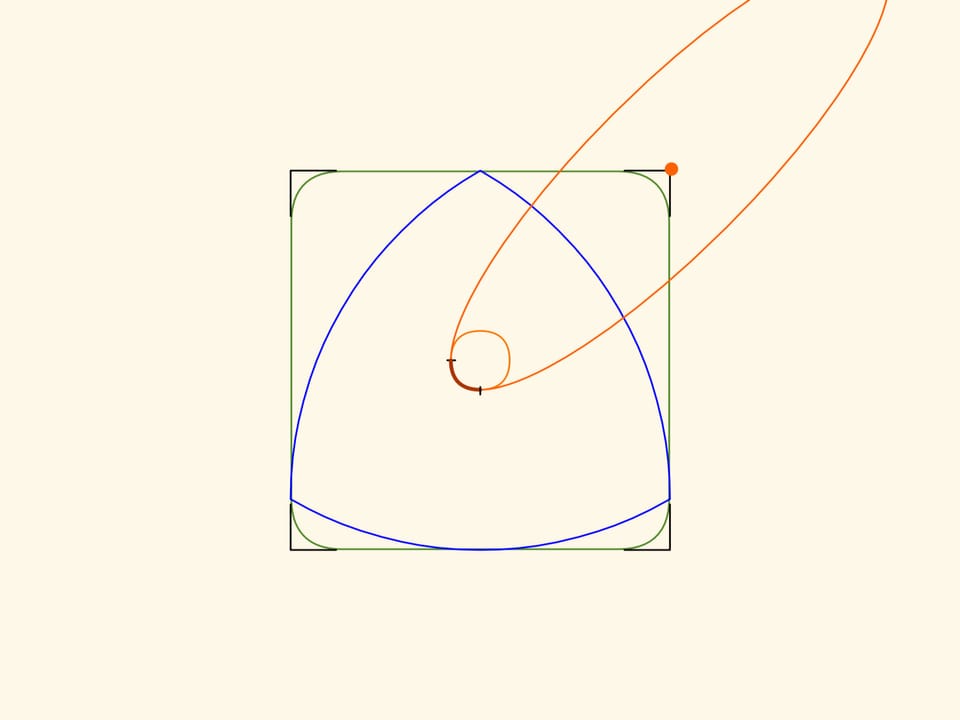
The film Circular Reuleaux triangle tells about the figures of constant width. The Reuleuaux triangle —, the simplest figure of constant width will help us to drill square holes. If one moves the center of the this «triangle» along some trajectory, its vertices will draw almost a square and itself will cover the area inside this figure.
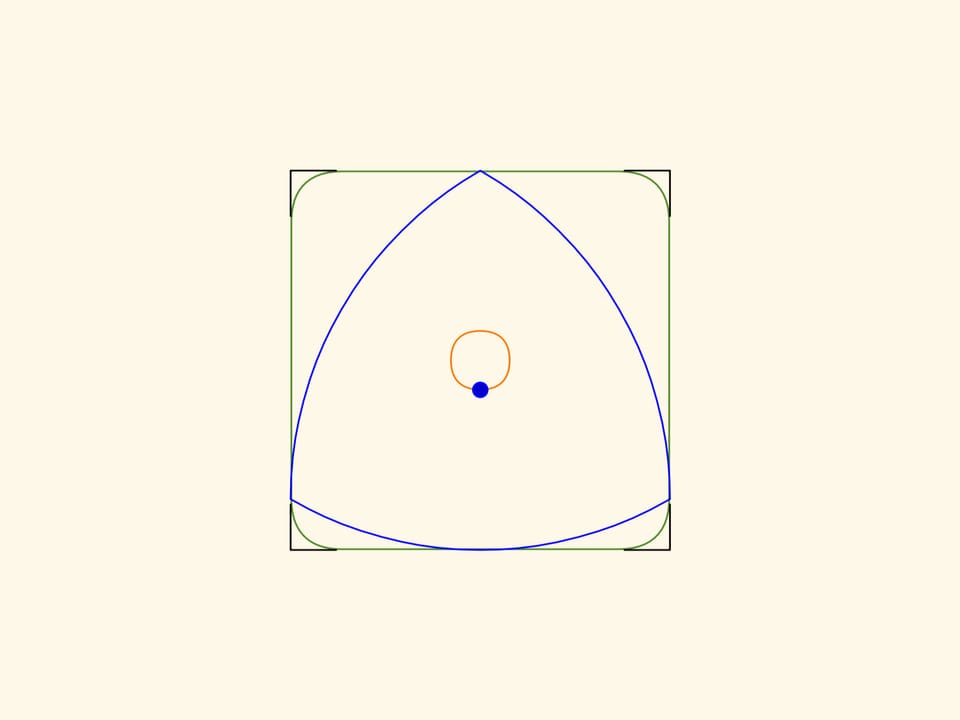
The borders of the obtained figure, except small angular pieces, will be straight segments! And if one extends the segments adding the corners, we get an exact square.
To achieve what we described above, the center of the Reuleaux triangle should move along the trajectory that consists of four equal patched arcs of ellipses. The centers of the ellipses are placed in the vertices of the square, the semi-axes forming an angle of $45^\circ$ with the sides of the square and equal $k\cdot(1+1/\sqrt{3})/2$ and $k\cdot(1-1/\sqrt{3})/2$ where $k$ is the side of the square.
The curves rounding the corners are also arcs of ellipses centered in the vertices of the square, semi-axes forming an angle of $45^\circ$ with the sides of the square and equal $k\cdot(\sqrt{3}+1)/2$ and $k\cdot(\sqrt{3}-1)/2$.
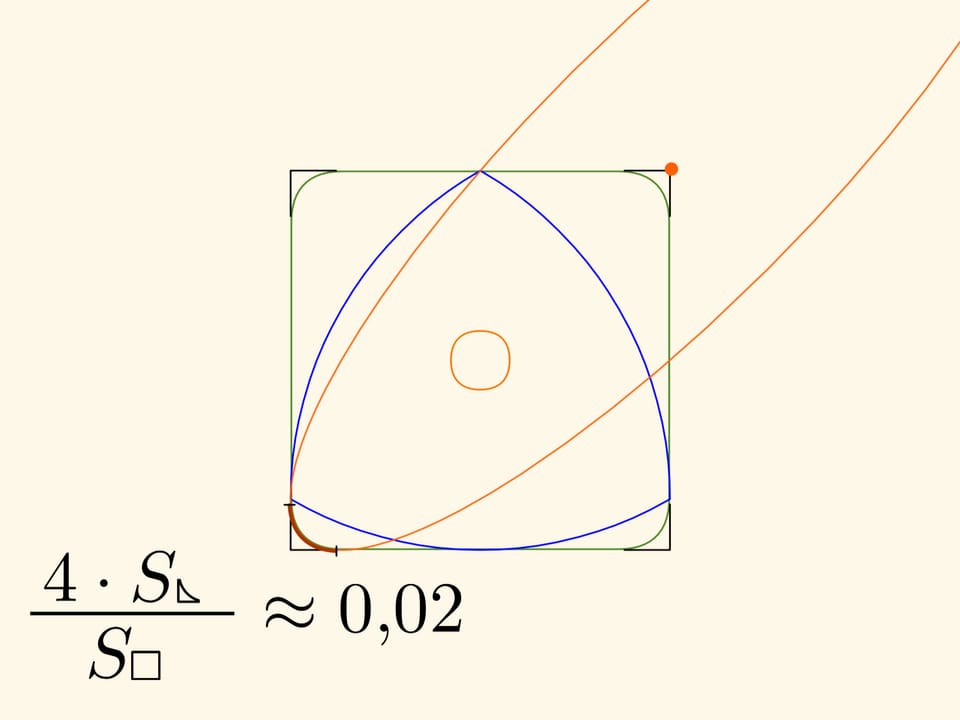
The area of the non-covered corners forms only around 2 percent of the area of the square!
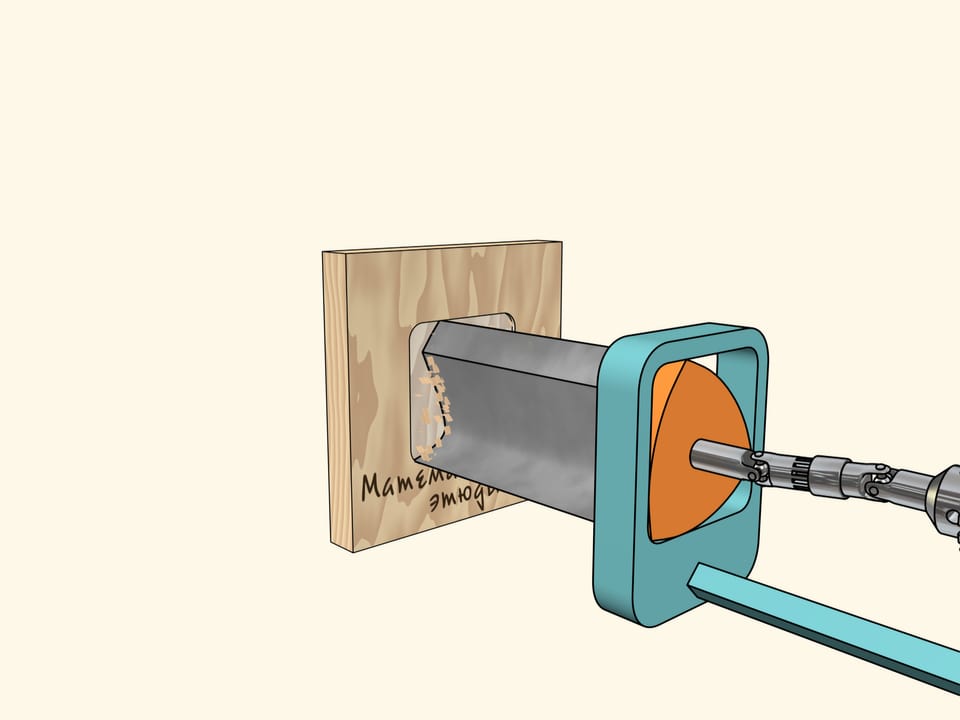
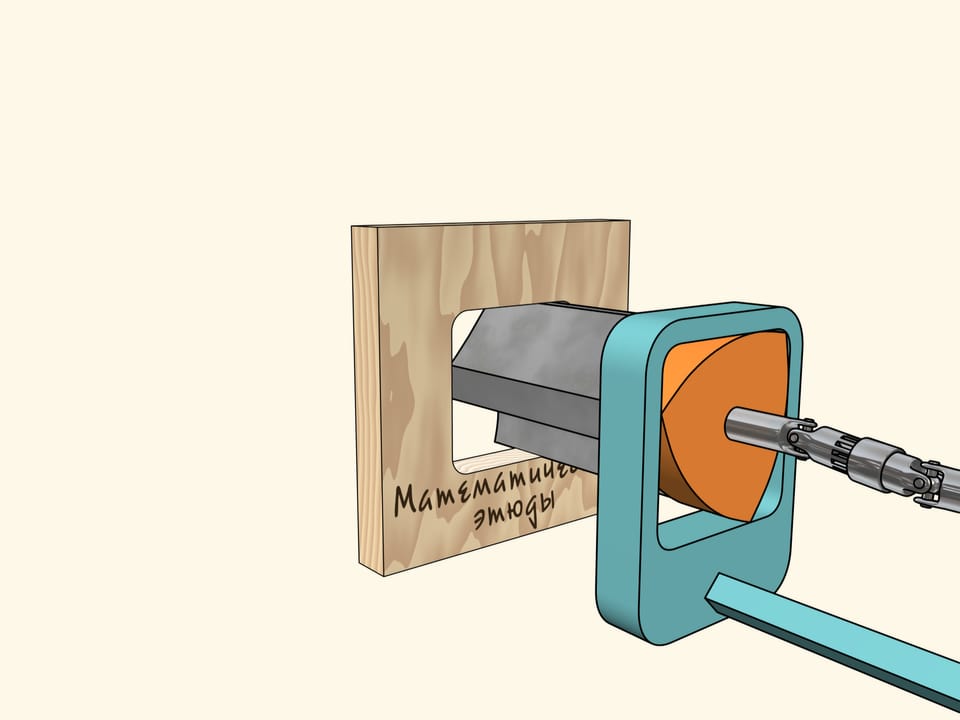
Now if one makes a Reuleaux triangle shaped drill, one will be able to drill square holes with slightly rounded corners but absolutely straight sides!
What is left is to make such a drill… Well, it's not hard to make the drill, its section should only remind of Reuleaux triangle and its cutting edges should coincide with its vertices!
The point is that its center's trajectory should consist of four arcs of ellipses, as we mentioned before. Visually this curve is very close to a circle and is even mathematically close to it, but it's still not a circle. In addition, all the eccentrics (a circle placed on a circle of different radius with a shifted center) used in technics provide circular motion.
In 1914 an english engineer Garry James Watts invents how to organize such a drilling. On a surface he places a directing template with a square cut in which the drill, «put freely into a chuck», moves. A patent for such a chuck had been given to a company that started manufacturing Watts drills in 1916.
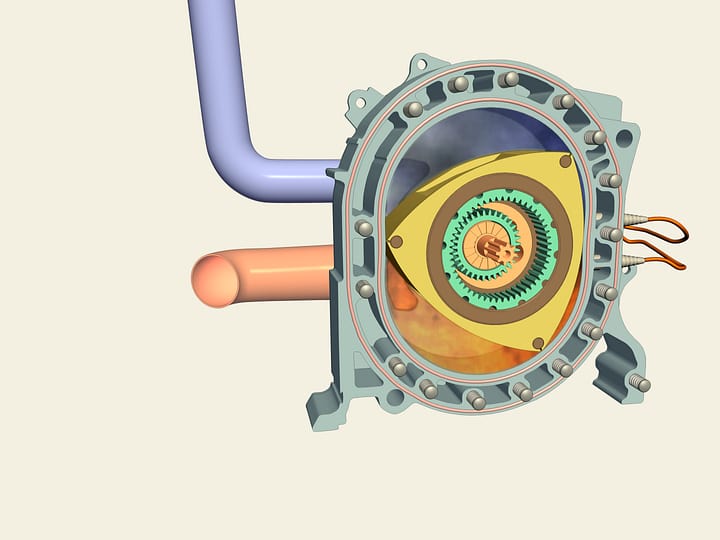
You should have already seen under the passing trucks what helps us: the drive shaft. his transmission is named after Gerolamo Cardano.
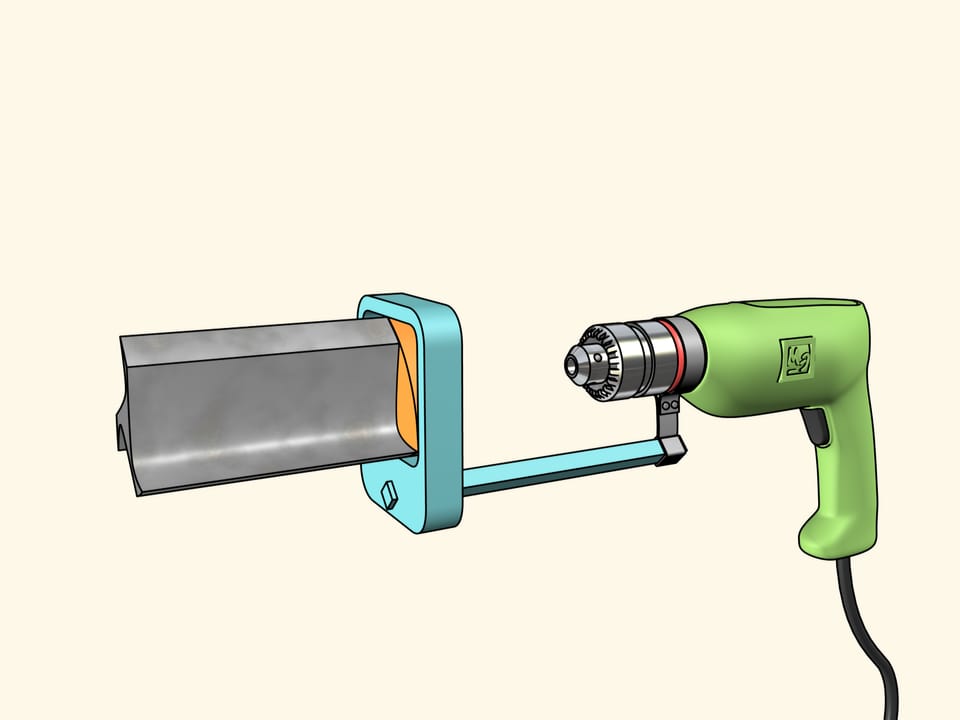
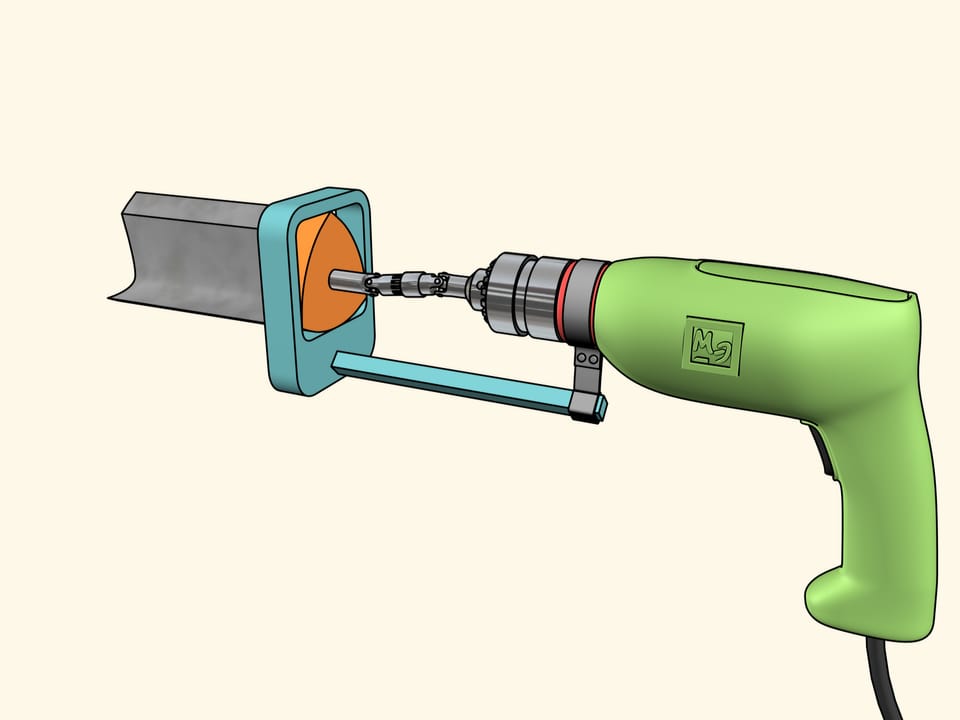
We'll use another known construction. Fix the drill to the Reuleaux triangle placed into a square directing frame. The frame is attached to the drill. It's left to transmit the drill chuck rotation to the Reuleaux triangle.
Gerolamo Cardano 1501—1576
When in 1541 the emperor Charles V triumphally entered conquered Milano, the rector of the doctors college Cardano was walking near the canopy.
In response to this honor he suggested to supply the royal carriage with a suspension with two shafts, the rolling of which would keep the carriage horizontal […]
To keep justice we have to mention that the idea of such a system goes back to antique times, at least the «Atlantic Codex» by Leonardo da Vinci has a drawing of a ship compass with a gimbal suspension.
Such compasses became widespread in the first half of the XVI century, apparently, without Cardano's influence.
S. G. Gindikin. Stories about physicists and mathematicians.
Now we have everything to start drilling. Take a sheet of veneer and… drill a square hole! As we've said before, the sides will be strictly straight and only the corners will be sightly rounded. If needed, on may correct them with a broach file.