It is common to speak of “exponential growth” when the aim is to emphasize the significant speed of change (growth or decline) of some value. If we consider time to be discrete and changing in leaps, then the concept of “exponential growth” is easily described using geometric progressions.
The most famous example, illustrating the speed of growth of a geometric progression, is the legend about the origin of chess. If you put one grain of wheat on the first field of the chess board, two — on the second, four — on the third and so on, then it turns out that filling the last 64-th field of the chess board requires to harvest crops from the entire Earth for more than a thousand years.
You can also get an idea of the speed of growth of a geometric progression just by folding a piece of paper. After the first fold the thickness of the paper would increase twice, after the second — 4 times, and if one could manage to fold the paper 42 times, the thickness of the paper would be greater than the maximal distance from the Earth to the Moon.
Examples demonstrating the decrease of the geometric progression are no less fascinating.
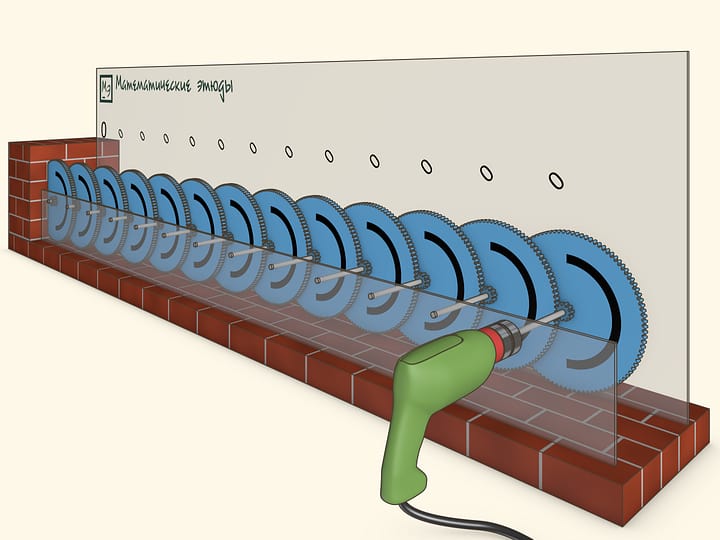
Imagine a sequence of gears connected successively in such a way that each gear is rotating 10 times less frequently than the previous one. If the first gear completed 10 full rotations, the second would complete a single one, the next one — 1/10 of a full rotation etc. Therefore, the angular velocities of the gears form a geometrical progression with common ratio 1/10.
In the movie the first gear turns with a rate of 3 full rotations per second. It turns out that even a few steps of the geometric progression are sufficient for the last gear nearly not to move in any “reasonable” time and it is even possible to completely fix it in a wall.
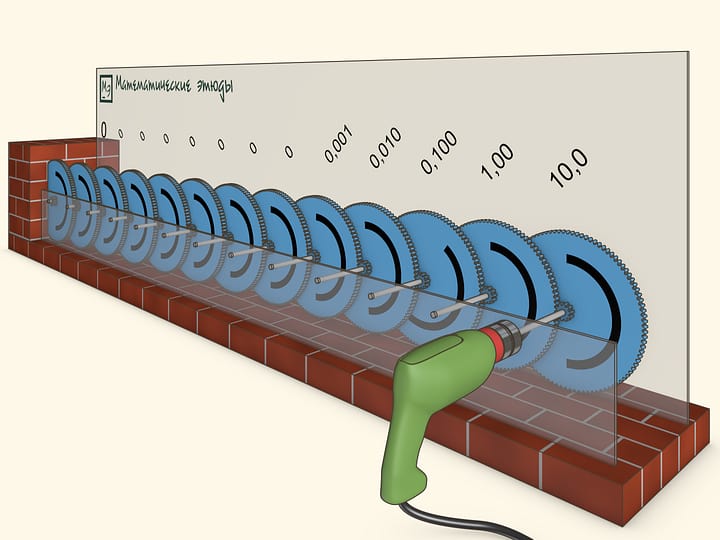
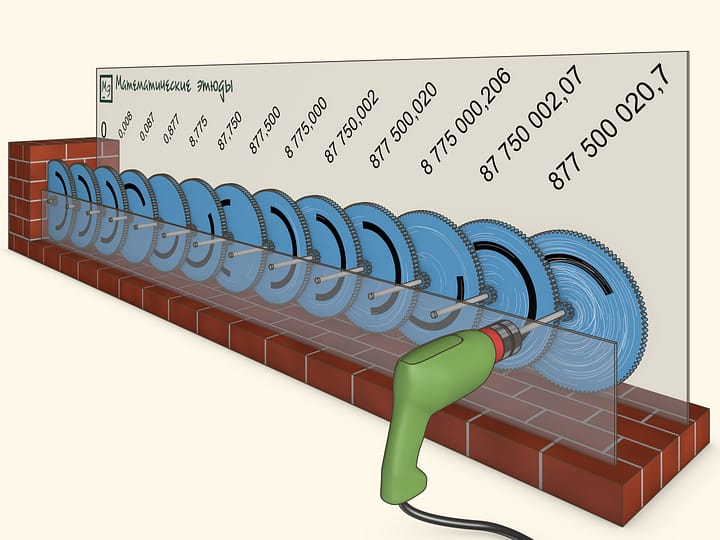
Let us watch how many rotations will the gears complete after a long time. For example, what will happen 10 years later...
After 10 years of the drill's constant work the first gear will have completed more than 877 million rotations, and the last, 13th, gear will not have budged even one thousandth of a rotation.
What would happen if we applied the drill to one of the intermediate gears? Despite the intuition suggesting that the gears to the right of the driven gear will move very fast, the system will not move at all. It turns out that the friction force emerging on the right side of the driven gear grows in a geometrical progression as well. Rotating such a system while applying force not to the rightmost gear is impossible.