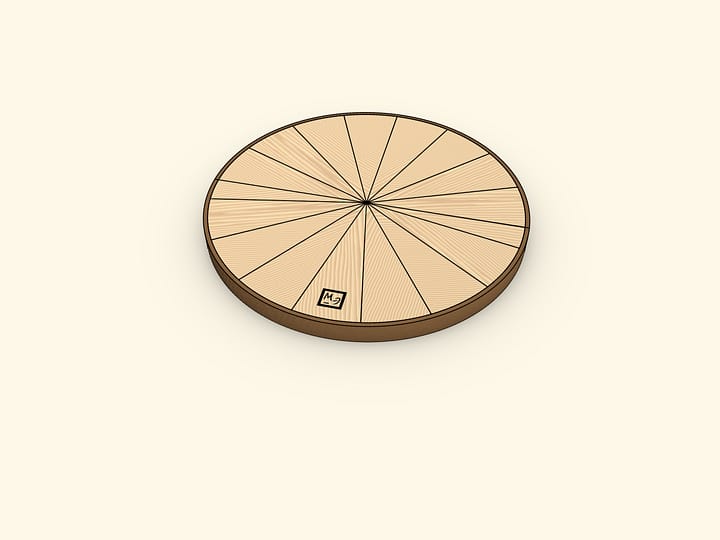
Area enclosed by a circle of radius $R$ is $S = \pi \cdot R^2$. Let's make sure of this, using the ability to calculate the area of a rectangle.
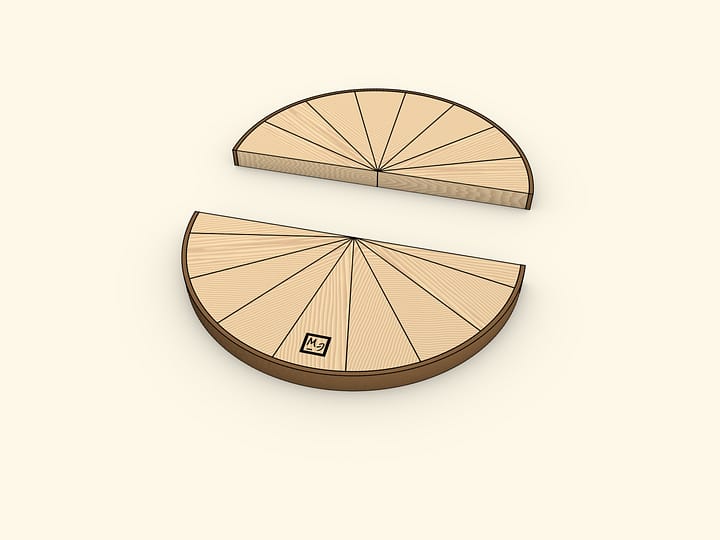
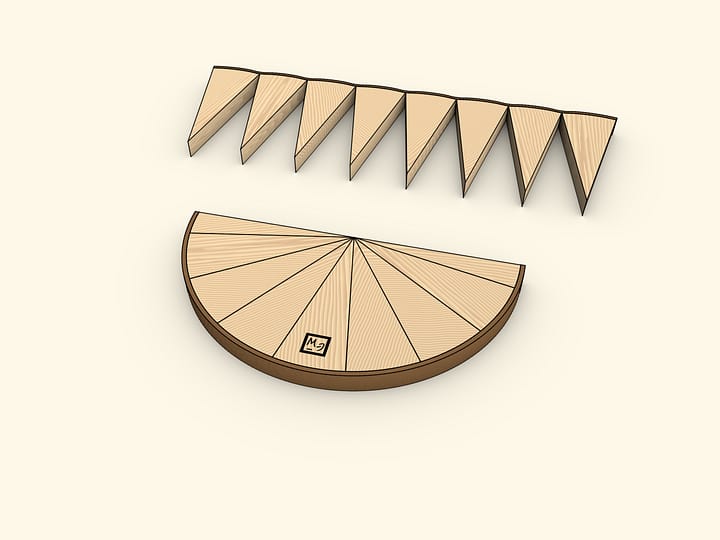
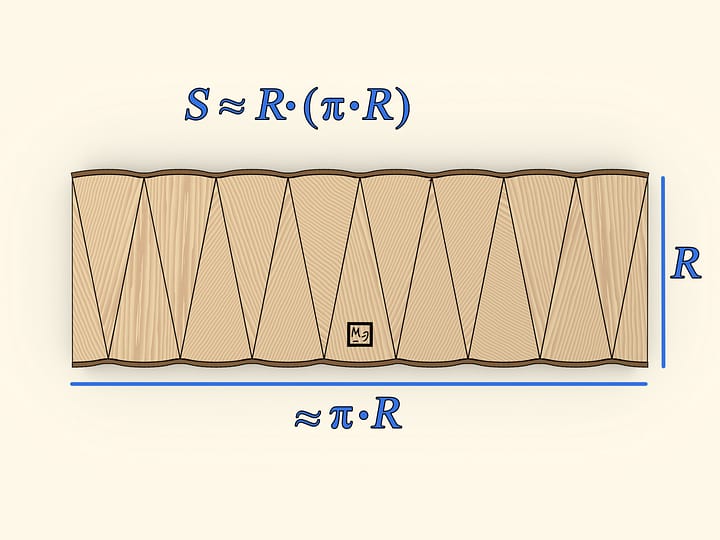
Divide the circle in two halves with its diameter. Divide each half into equal sectors. ”Opening” the halves and inserting one into the other, one gets a shape of the same area that of the initial circle. This shape is almost a rectangle. Almost — because the longer sides are not quite straight. These sides are half the length of the circle long, that is, $\pi \cdot R$. The short side of the shape obtained is exactly as long as the radius of the initial circle. Rectangle area is given by the product of its sides' lengths: $S≈(\pi \cdot R)\cdot R = \pi \cdot R^2$.
We've used the formula for the area of a rectangle, though the shape obtained is not exactly a rectangle, thus the approximate equality sign. It is clear though that if the circle is divided into a larger number of equal parts, the difference from a rectangle would get lesser and lesser. In the limit, the shape wouldn't differ from a rectangle, so this model is not only illustrative, but also quite valid.
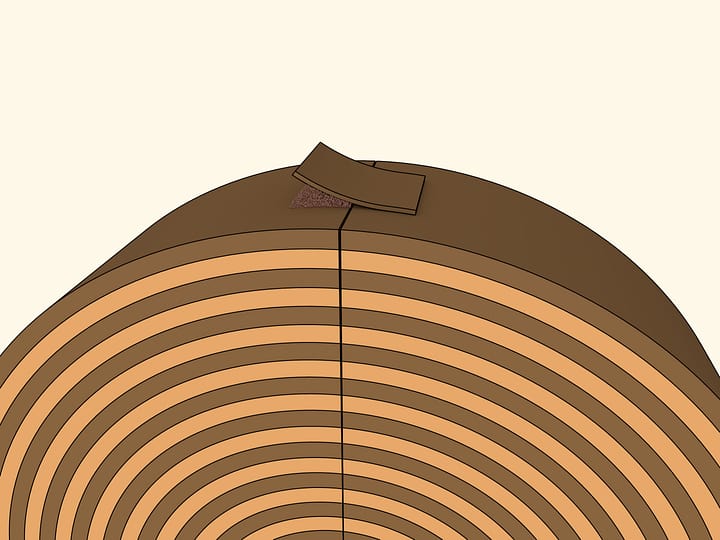
The model can be manufactured from wood and a stripe of leather. The latter should be picked of a different color than the wood's, so that the circumference and the rectangle's long sides were clearly distinguishable. In one of the two parts, one sector should be divided in two halves — so that the external pieces were halves of standard sectors. Then the shape obtained would look more like a rectangle when put together, otherwise — like a parallelogram.
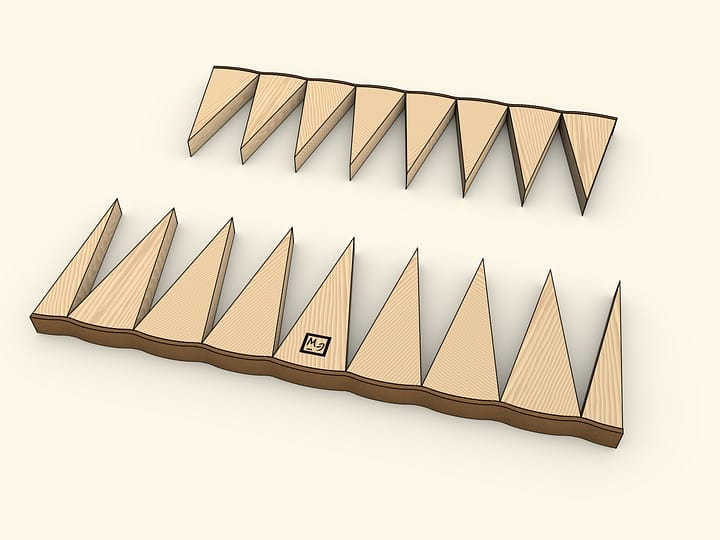
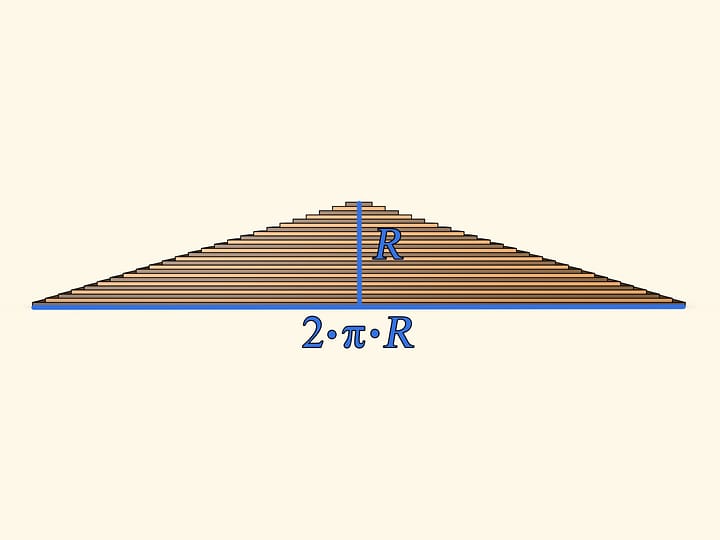
To use the formula for the area of a triangle, assemble a circle of concentrically arranged stripes of, say, leather. The external one should be the longest, next one — a bit shorter etc. Lengths should be chosen so that the circle is formed when wrapping a circle. The stripes' ends meet along one radius.
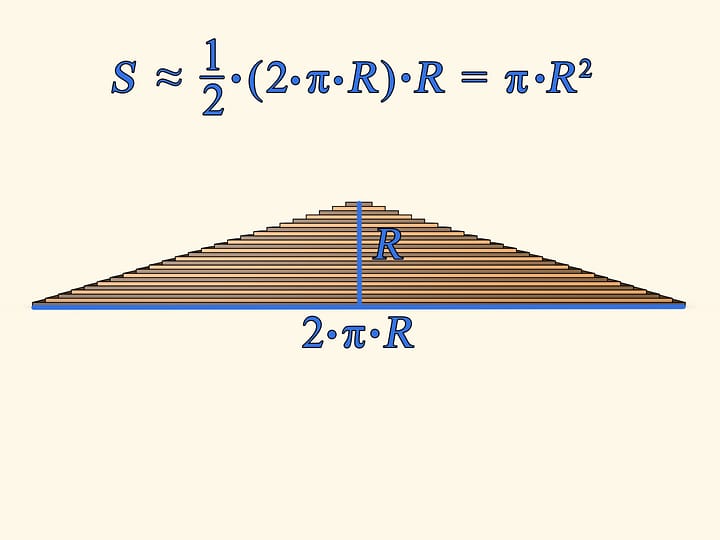
Now unwrap all the stripes at once and the circle turns into almost a triangle. "Almost" — because its legs are not straight lines, but are comprised of steps. Several formulae for finding the area of a triangle are studied at school (and all of them provide the same answer!). Let us use one of those — the area of a triangle equals half of a product of side length (of the base, for example) by the length of its altitude. The base length in our case exactly equals the length of the initial circle's circumference, that is $2 \cdot \pi \cdot R$. The altitude is simply the circle's radius. Thus the area of the shape is $S ≈ (1/2) \cdot (2 \cdot \pi \cdot R) \cdot R ≈ \pi \cdot R^2$.
We've used a formula for the area of triangle, though the shape obtained is not exactly a triangle, that's why the equality is approximate. It is nevertheless clear that if the circle is composed of thinner and thinner stripes, the steps on triangle's legs will be smaller. And in the limit the shape will not differ from a triangle, so the reasoning is quite valid.