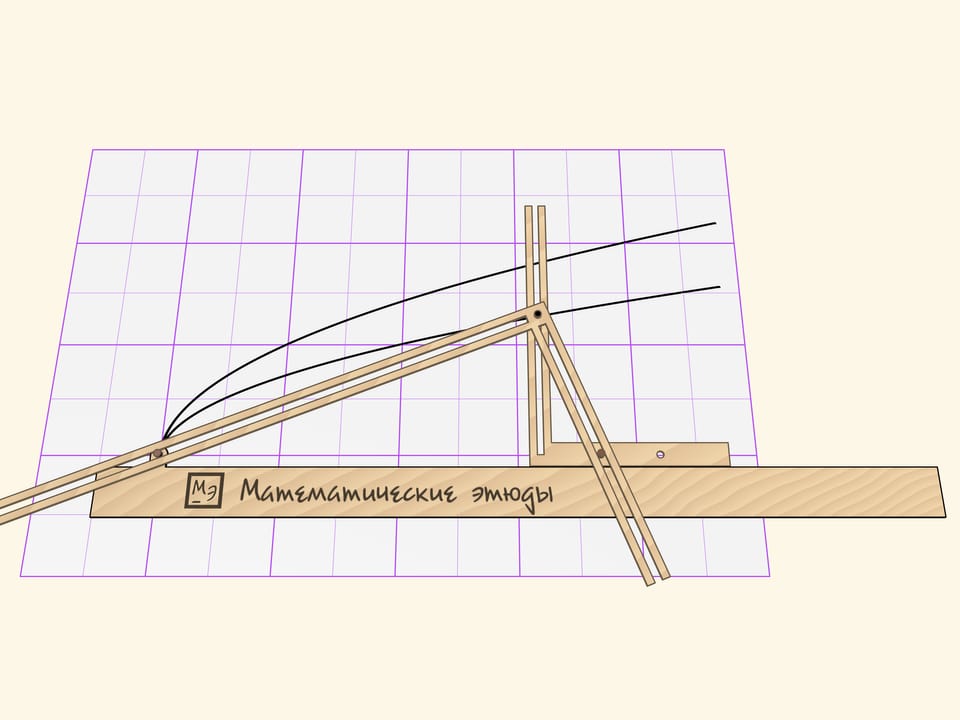
A beautiful tool for drawing a parabola was invented by an Italian mathematician Bonaventura Cavalieri (it. Bonaventura Francesco Cavalieri, lat. Cavalerius, , 1598—1657) back in the XVII century.
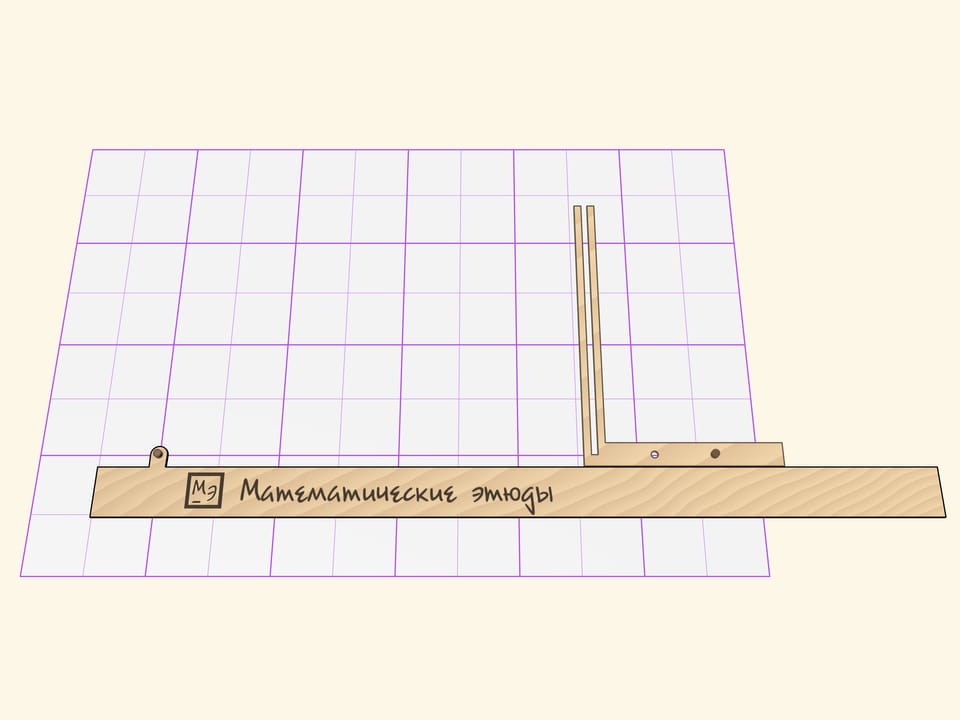
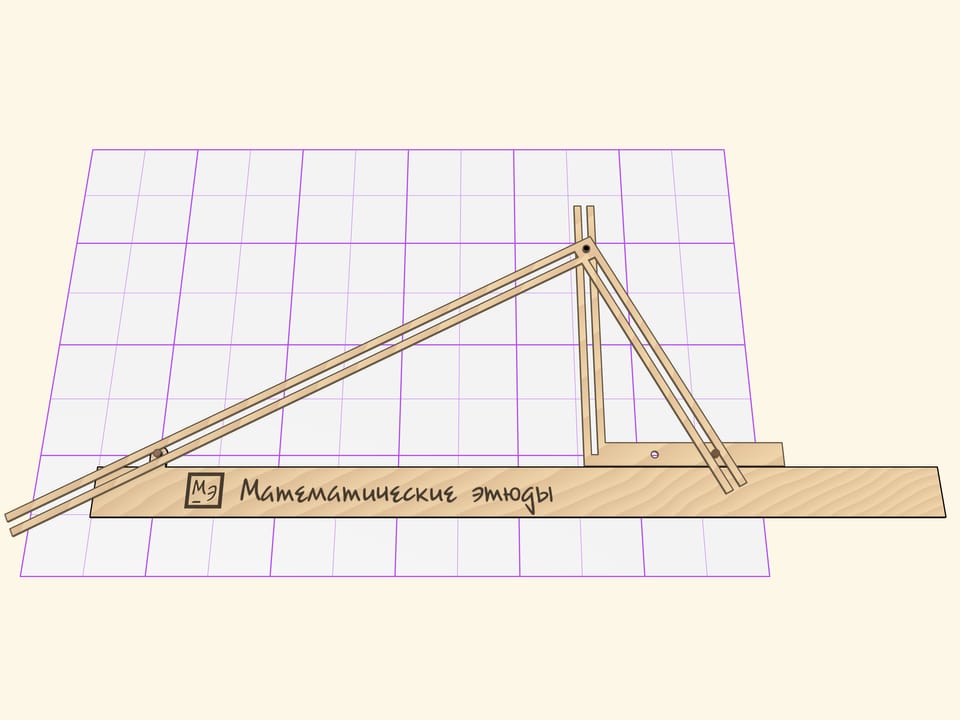
The Cavalieri’s parabolograph consists of three parts: a ruler and two rigid right angles with slots on their sides.
One right angle slides on a ruler, which is fixed relative to a sheet, in such a way that its horizontal side constantly touches the ruler.
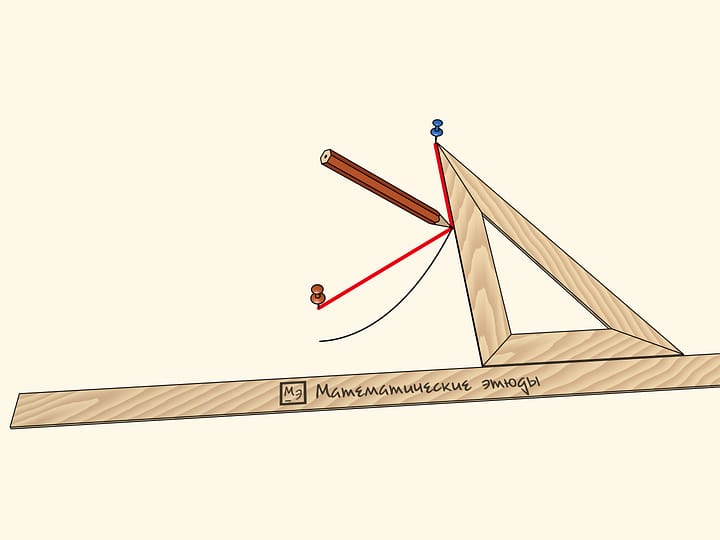
The second right angle forms a right triangle with the ruler. The right angle vertex is equipped with a stylus and slides along the slot of the first right angle vertical side. Two other sides of the second right angle slide their slots on the guide pins, one of which is fixed to the ruler, and the other — to the horizontal side of the movable angle.
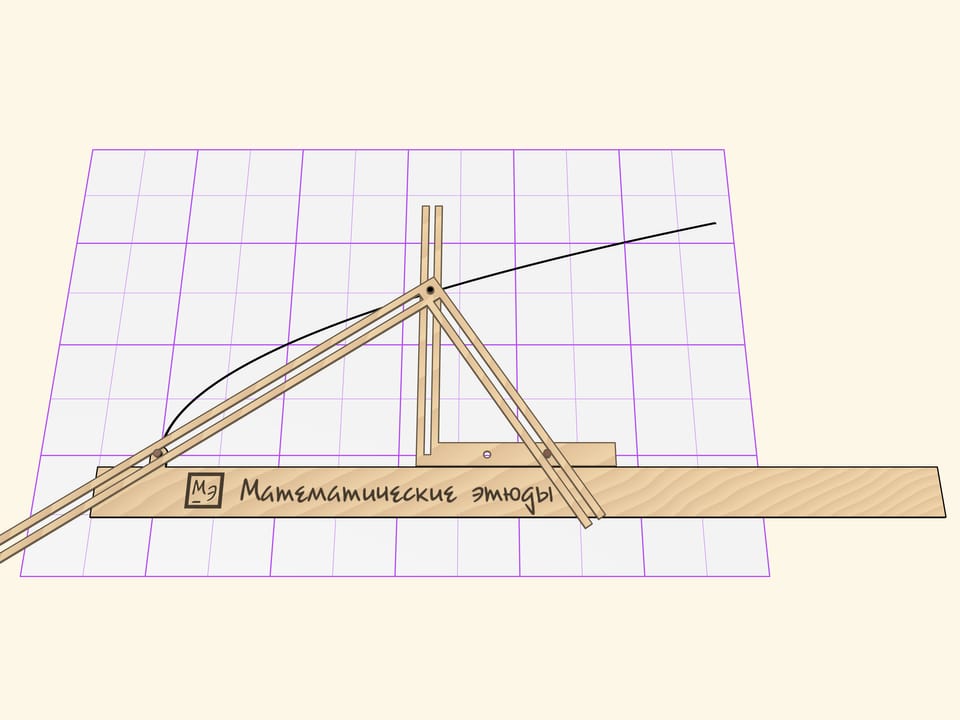
When the Cavalieri’s parabolograph is moving, the stylus is drawing a parabola. The distance from the pin to the vertex of the right angle, which is adjacent to the ruler, is a parameter of the parabola. The curve changes then the pin is moved, but it remains being the parabola.
The proof that the curve being drawn is the parabola is based on the theorem from the modern school mathematics course. Consider the triangle formed by the sides of the second right angle and the ruler. In this triangle, the square its altitude length (the distance from the stylus to the ruler), dropped on its hypotenuse is equal to a product of catheti projections on the hypotenuse. The projection of the “right” сathetus is constant by the parabolograph design and it is the parameter that defines the parabola.