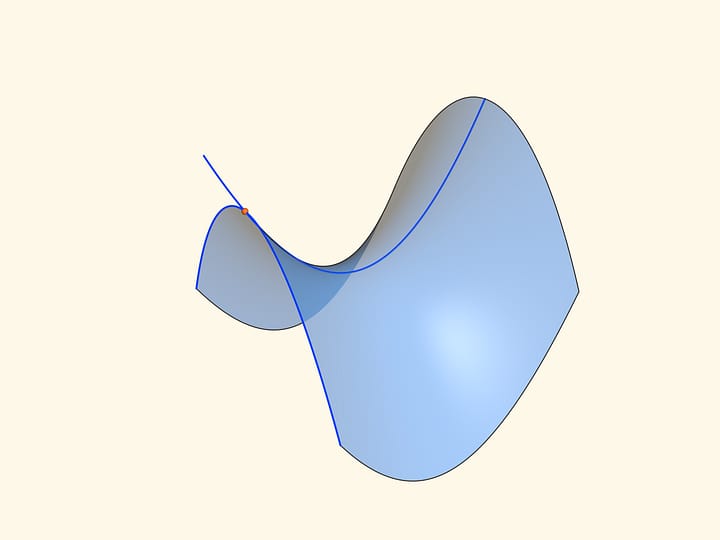
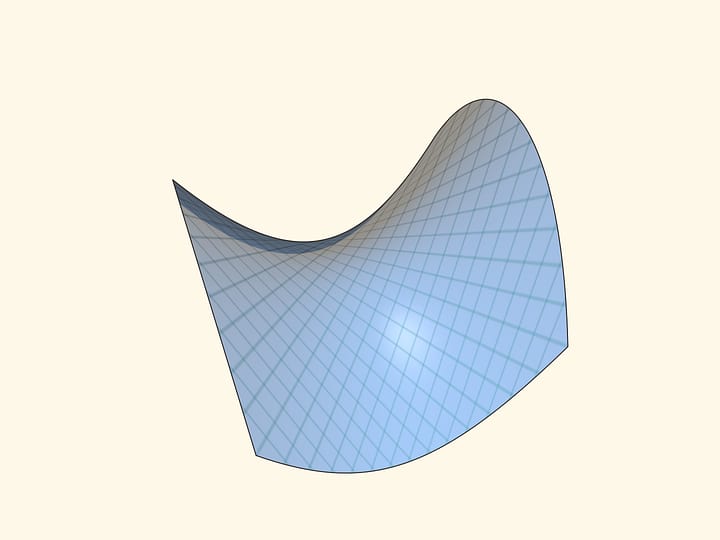
A hyperbolic paraboloid is a surface, which looks like a saddle. It is formed during such a movement of a parabola open down that its top glides on the other static parabola open up. Planes containing parabolas are perpendicular at every moment, while the axes are parallel.
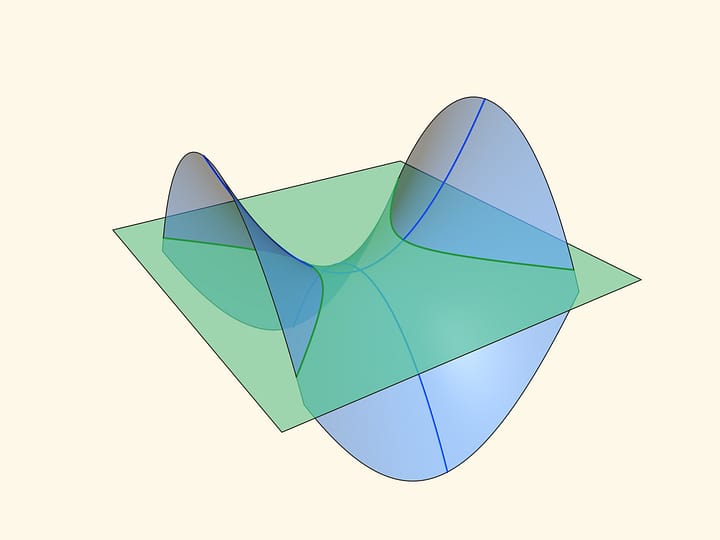
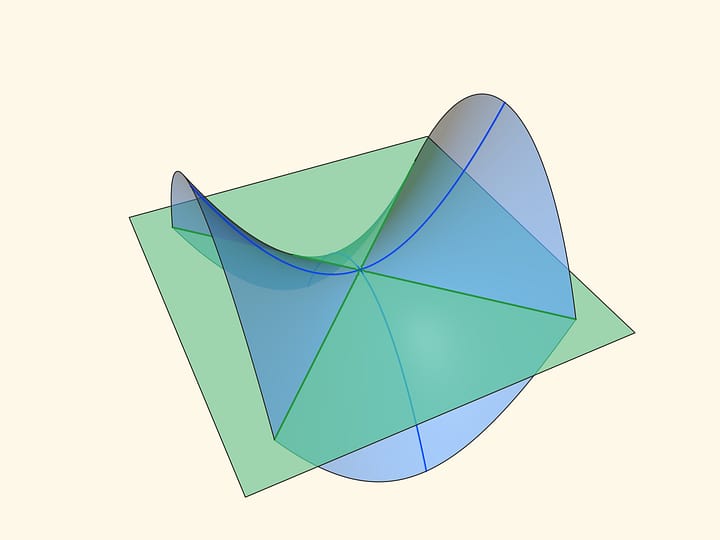
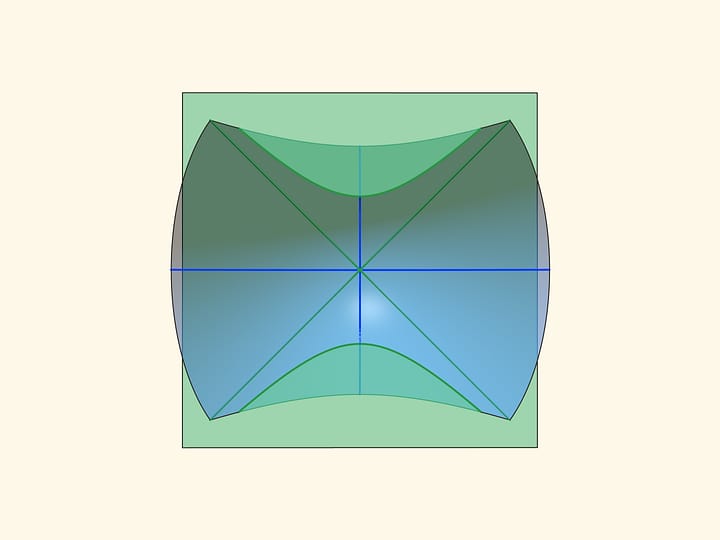
When a hyperbolic paraboloid crosses any horizontal plane, a hyperbola is formed. If a plane passes through the centre of a saddle, a hyperbola degenerates into a pair of intersecting straight lines (if we project a hyperbola from a parallel section on this plane, the straight lines will be an asymptote of a hyperbola-projection).
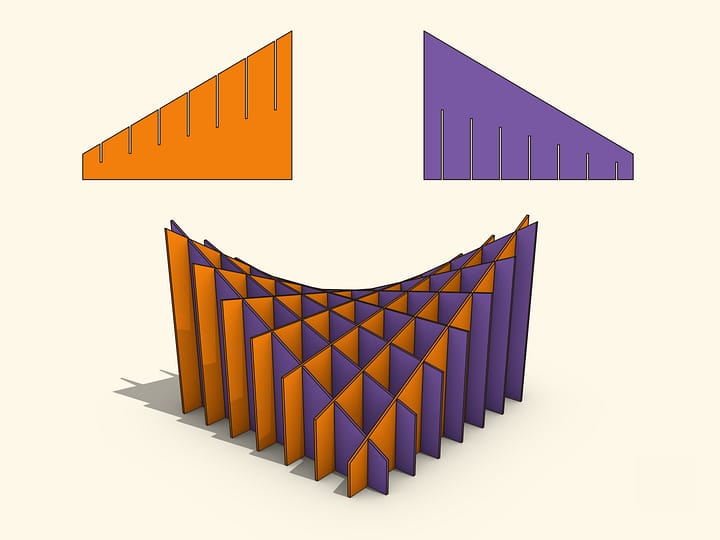
It turns out that a hyperbolic paraboloid is a ruled surface, which can be also formed by movement of a straight line!
Let’s draw a set of segments between two parallel lines at equal distances. Then let’s rotate straight lines around the central segment in opposite directions (lengths of all segments, except the central, will change). So the segments positioned in space this way all lie on a hyperbolic paraboloid.
This surface can be beautifully realized as a model made of thin tubes.
The Gaussian curvature is negative at every point of a hyperbolic paraboloid. These surfaces are also called saddle, as they are visually similar to saddles for horse-riding.