Если «прожигать» CD– или DVD–диск на компьютере, то записанная часть «болванки» выглядит более темной, чем неиспользованная.
Чего больше на диске, изображенном на картинке в начале фильма, — записанной информации или свободного места?
С точки зрения математики, и CD-, и DVD–диск — это кольцо. Радиус внутренней окружности, ограничивающей круг, на который ничего не пишется, равен 2 сантиметрам, а радиус всего стандартного диска — 6 сантиметрам. Информация записывается по спиральной дорожке, разматывающейся от меньшей окружности к большей. Так как одинаковому количеству информации соответствует одинаковая длина дорожки, то объём информации, записанной на «болванку», пропорционален площади занятого кольца.
Начнём «прожигать» диск так же, как это делает компьютер. Если ширина записанного кольца будет равна ширине незаписанного и составлять по 2 сантиметра, то видно, насколько площадь использованной части меньше свободной. При этом, даже если к площади записанного кольца добавить площадь всего внутреннего круга, на который ничего не пишется, то их суммарная площадь всё равно будет меньше площади незаписанной части «болванки».
Для того чтобы была занята ровно половина «болванки», внутреннее кольцо должно иметь ширину, приблизительно равную 2,5 см, а внешнее кольцо — около 1,5 см.
Отчего же возникает такой эффект?
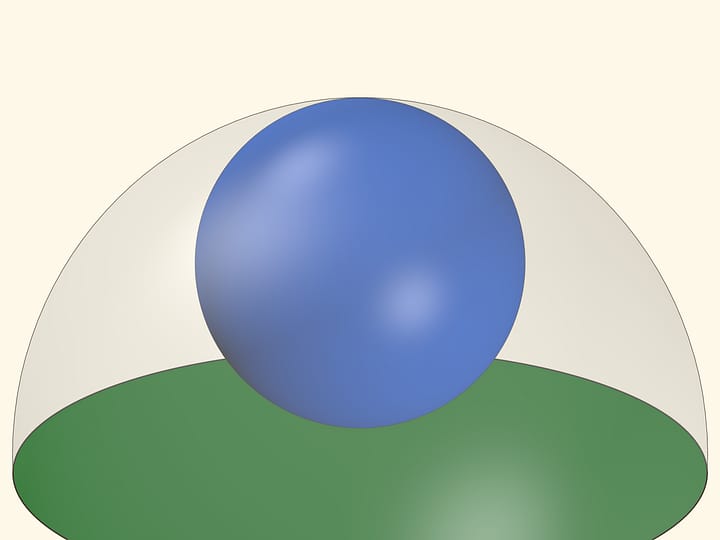
На плоскости шаром является круг и, соответственно, объём есть площадь этого круга. Как вы все хорошо знаете, площадь круга радиуса $R$ равна $\pi R^2$. Чтобы посчитать площадь кольца, нужно из площади большого круга вычесть площадь неиспользуемого маленького — $\pi\cdot(R^2-r^2)$. И так как всё зависит от радиуса, да ещё в квадрате, то, чем ближе к большему радиусу описано кольцо, тем больше, при той же ширине, его вклад в площадь.
В нашем трёхмерном пространстве объём шара зависит от радиуса, возведённого в третью степень. А значит, и рассматриваемый эффект становится ещё более выраженным: бóльшая часть объёма шара сосредоточена рядом с границей!
Чего больше по объёму в этом апельсине — кожуры или мякоти? Кожура занимает, казалось бы, не очень толстый слой, но он расположен рядом с границей шара. И его объём на приведённом рисунке равен объёму всей вкусной части апельсина. Покупая апельсин с толстой кожурой, по объёму вы приобретаете в основном кожуру.
Смотри также
Объём шкурки апельсина // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 92, 326—327.