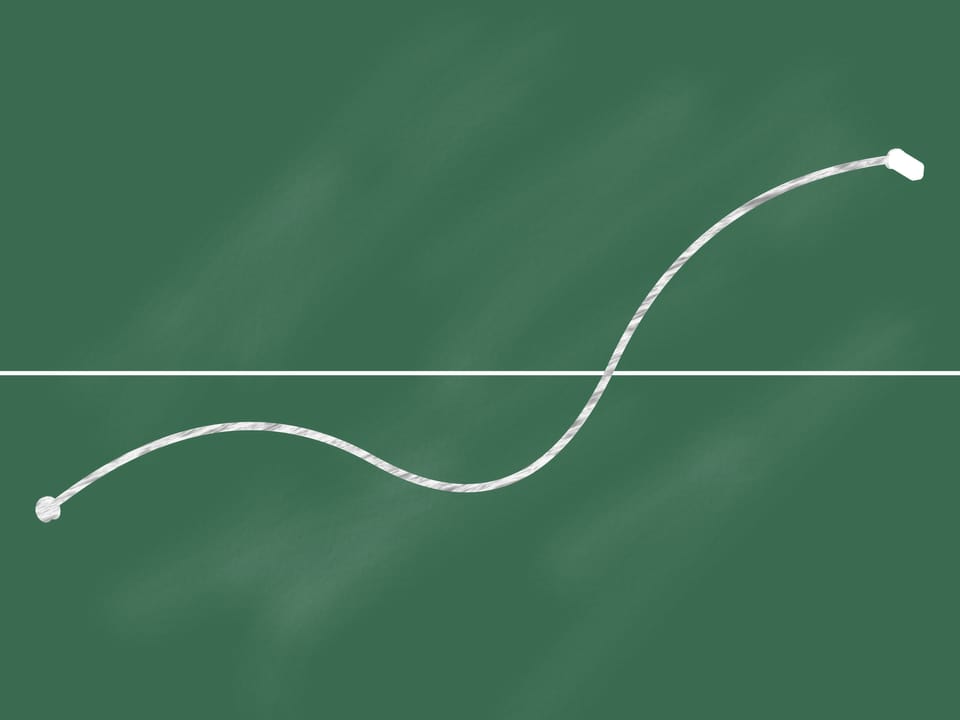
Sulla lavagna tracciamo una retta orizzontale che la divide in due parti. Segniamo due punti, uno situato nella parte inferiore e uno in quella superiore.
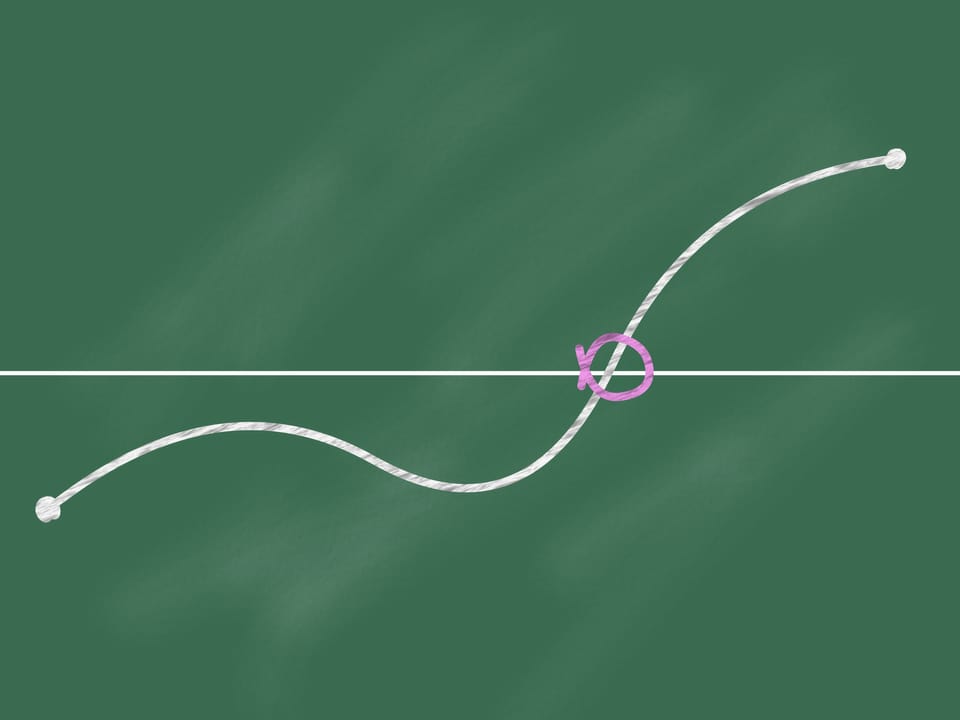
Uniamo questi punti per mezzo di una linea continua (cioè non staccando mai il gesso dalla lavagna). Allora in un certo punto (che può essere non unico) la nostra linea interseca la retta orizzontale.
Pensereste voi che questo fatto ovvio anche per i bambini può essere utile in matematica? Nonostante l'apparente ovvietà, questa proposizione è un teorema, precisamente il teorema di Bolzano-Cauchy, e richiede una dimostrazione.
Non daremo qui la dimostrazione di questo teorema, ma osserveremo soltanto che tutte le sue ipotesi sono importanti, ossia necessarie. Se la linea non fosse continua (se cioè fosse consentito staccare il gesso dalla lavagna) è ovvio che si potrebbe saltare dalla parte inferiore a quella superiore della lavagna, senza attraversare la retta orizzontale. Se non si fosse considerata l’intersezione con la retta orizzontale (che rappresenta l’insieme di tutti i numeri reali), ma, per esempio, l’intersezione con l’insieme dei soli numeri razionali, allora di nuovo l’intersezione si sarebbe potuta evitare.
La cosa più sorprendente è che questa osservazione apparentemente infantile è uno strumento molto potente usato nella dimostrazione di alcune proposizioni matematiche. L'inconveniente sta nel fatto che la dimostrazione non è di tipo costruttivo : la linea da qualche parte attraverserà la retta orizzontale, ma in che punto esattamente, data una precisa linea continua, è impossibile dirlo usando questo teorema.
Alcuni esempi dell’utilizzo del teorema di Bolzano-Cauchy saranno mostrati nei film della sezione “Continuità”