Il numero dei gradi di libertà è la quantità di parametri indipendenti che definiscono in modo univoco lo stato di un sistema meccanico.
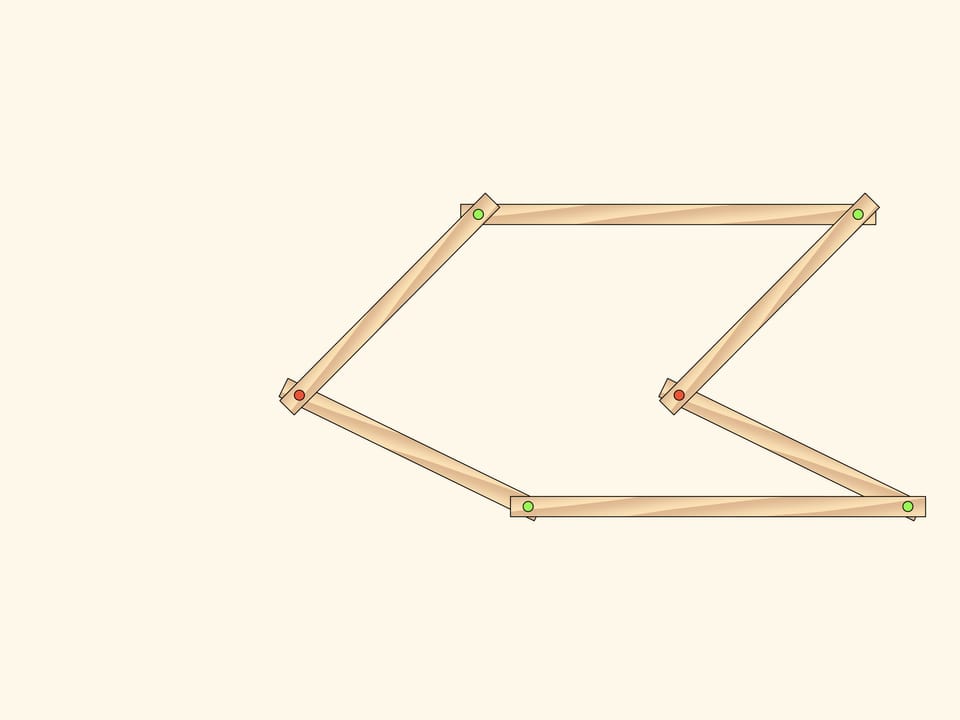
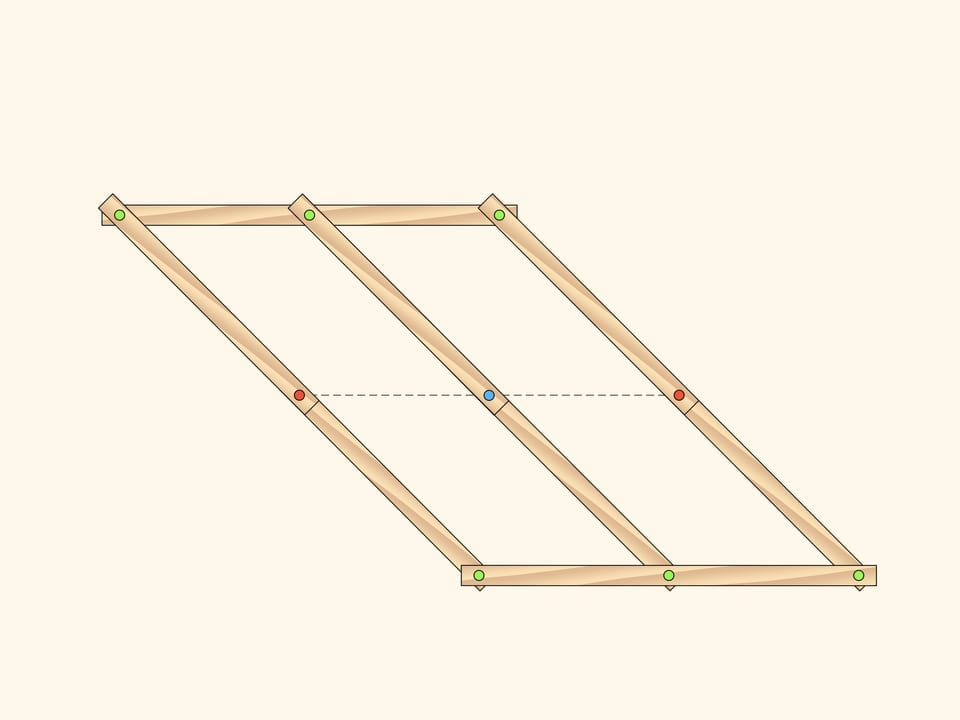
Consideriamo un meccanismo planare a cerniere, che consiste di due parallelogrammi identici, aventi in comune un lato e due cerniere, fisse, alle sue estremità (marcate in rosso). Il numero di gradi di libertà di questo meccanismo è, ovviamente, uguale a due, perché i parallelogrammi possono inclinarsi indipendentemente l’uno dall’altro, e come parametri si possono scegliere, per esempio, gli angoli di inclinazione dei parallelogrammi, misurati a partire dall’orizzontale.
Dato uno specifico meccanismo, è sempre definito il numero dei suoi gradi di libertà? Oppure esistono dei meccanismi che hanno un numero variabile di gradi di libertà? La risposta è che esistono…
Il primo meccanismo planare a cerniere con un numero variabile di gradi di libertà fu inventato da V. Vunderlikh nel 1954. Era composto di due cerniere fisse e 12 barre. Noi considereremo un meccanismo più semplice, con 9 barre, inventato dal matematico russo Mikhail Kovalev.
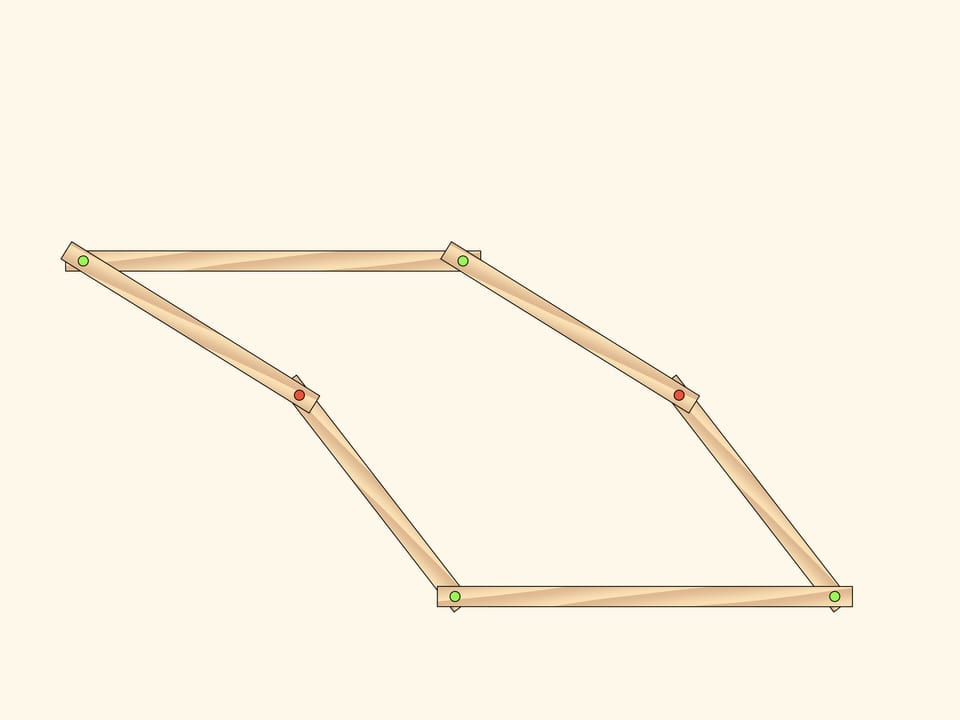
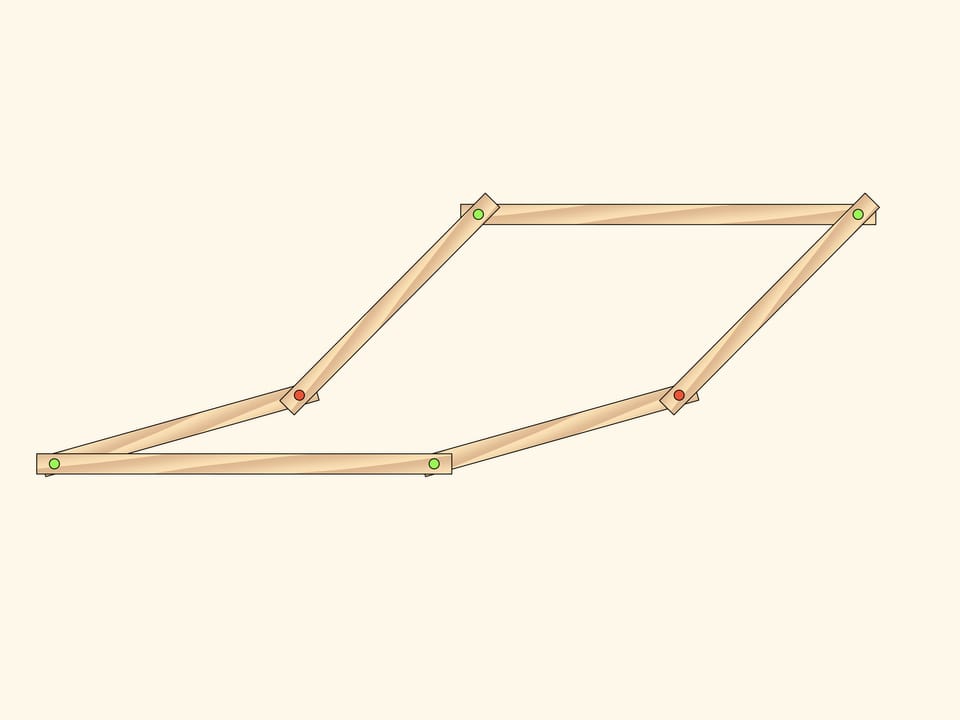
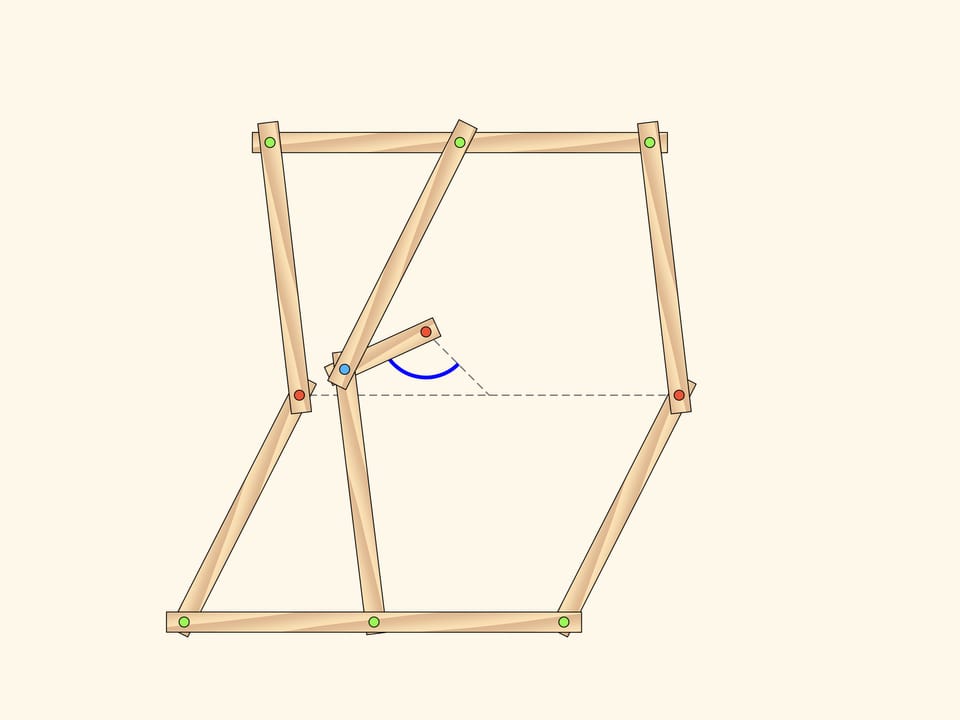
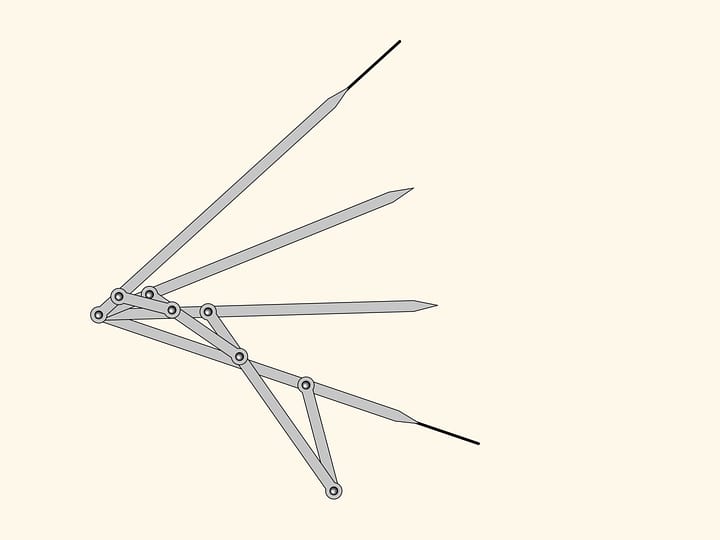
Aggiungiamo al parallelogramma doppio, composto dall’unione dei due parallelogrammi che abbiamo considerato, una “linea mediana spezzata”, composta di due barre uguali unite da una cerniera. Ed a questa cerniera aggiungiamo una barra corta, la cui seconda estremità verrà fissata con una cerniera (in rosso) al piano.
Finché la cerniera blu rimane sul segmento centrale che unisce le due cerniere rosse iniziali, l’aggiunta della barra non incide sulla quantità di gradi di libertà del meccanismo. Il suo stato è dato, per esempio, dai due angoli di inclinazione dei parallelogrammi.
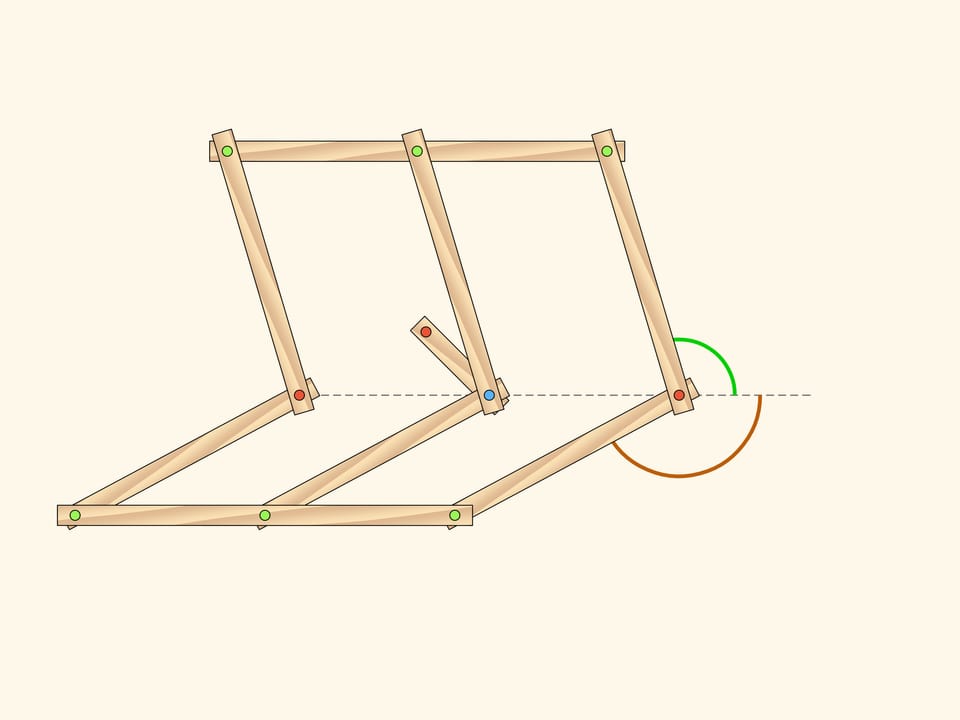
Tuttavia la cerniera blu può uscire dal segmento centrale nel momento in cui le barre mediane e la barra piccola si trovano tutte sulla stessa retta. E appena la cerniera blu esce dal segmento centrale, lo stato di tutto il meccanismo è definito da un solo parametro! In qualità di questo parametro si può scegliere, per esempio, l’angolo tra la posizione della barra corta aggiunta e la sua posizione iniziale.