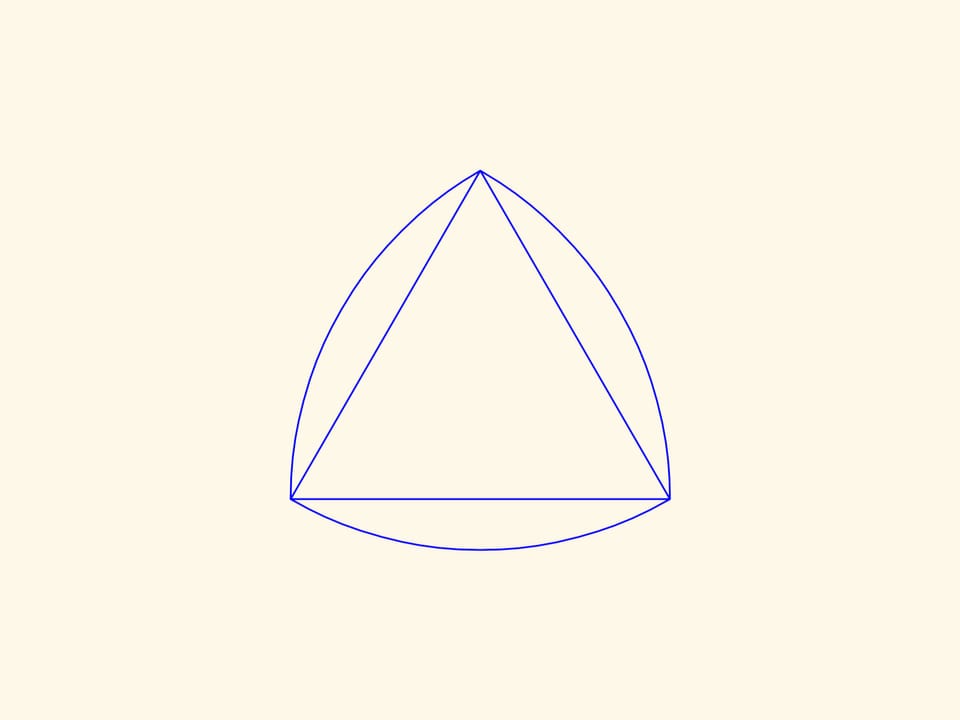
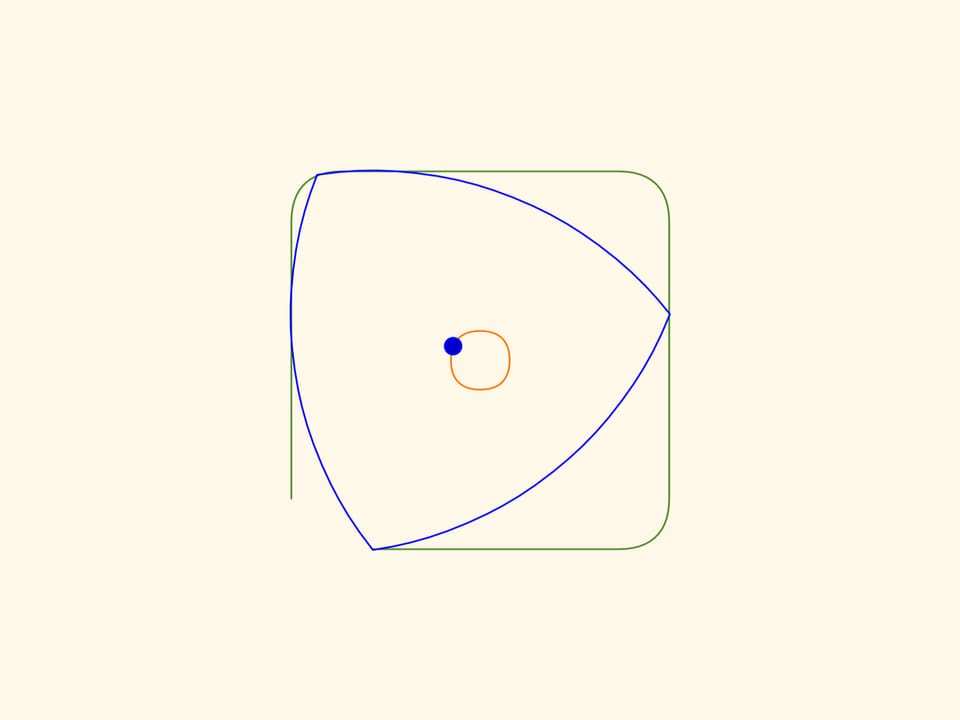
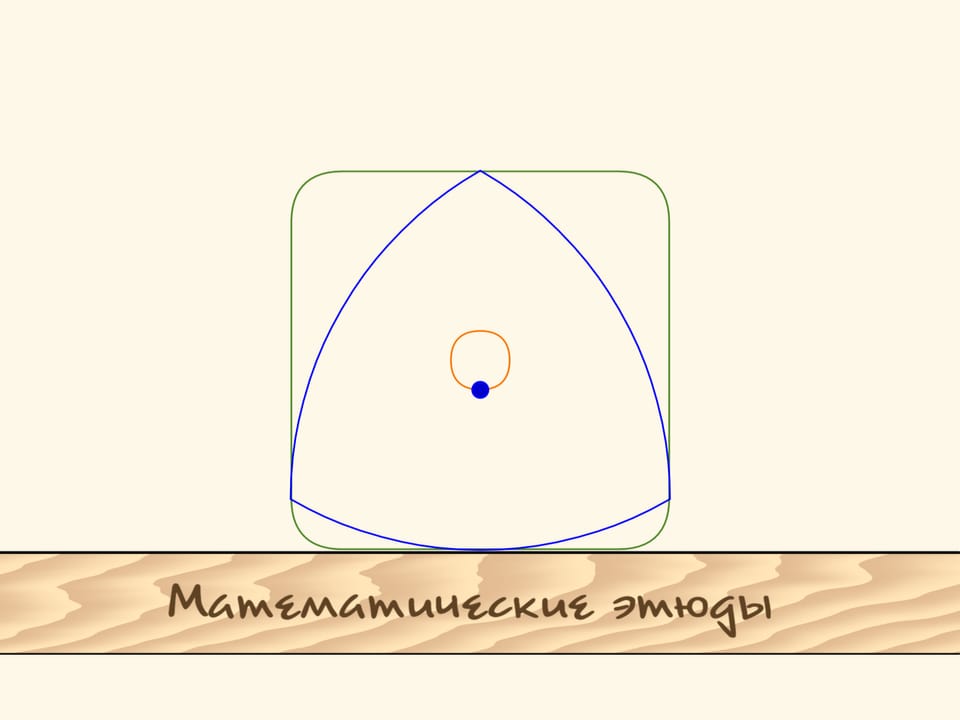
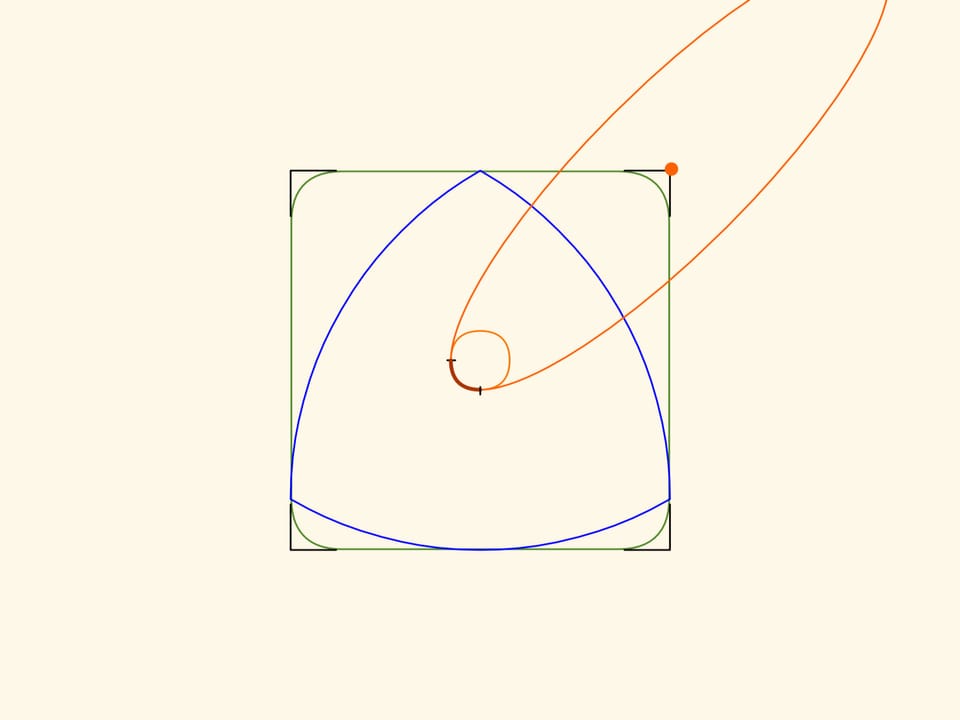
Nel filmato Il triangolo curvo di Reuleaux abbiamo visto delle figure che hanno una larghezza costante. Che il triangolo di Reuleaux sia la figura più semplice di larghezza costante ci aiuterà a realizzare dei fori quadrati. Se si fa muovere il centro di questo “triangolo” lungo una certa traiettoria, i suoi vertici disegnano quasi un quadrato, e lo stesso triangolo spazza tutta l’area all’interno della figura così ottenuta.
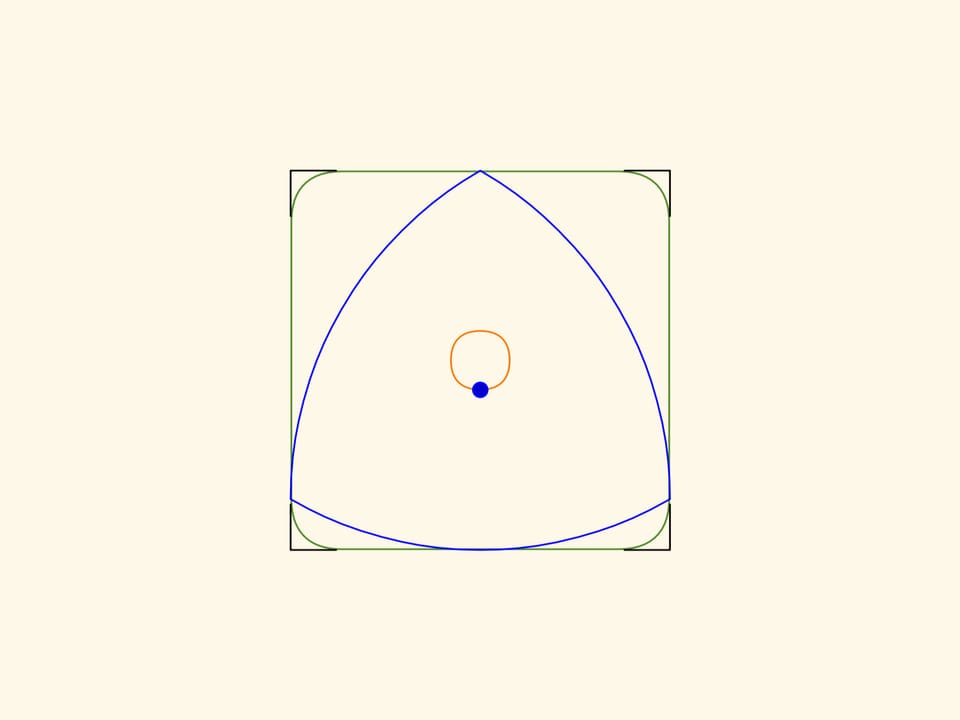
I bordi della figura ottenuta, fatta eccezione per dei piccoli tratti sugli angoli, saranno rigorosamente rettilinei! E prolungando questi segmenti rettilinei si ottiene esattamente un quadrato.
Al fine di ottenere ciò che abbiamo descritto, il centro del triangolo di Reuleaux deve muoversi lungo una traiettoria, che è l’unione di quattro archi uguali di ellissi. I centri delle ellissi sono situati sui vertici del quadrato mentre i semiassi sono ruotati di $45^\circ$ rispetto ai lati del quadrato, e sono uguali a $k\cdot(1+1/\sqrt{3})/2$, $k\cdot(1-1/\sqrt{3})/2$, dove $k$ è la lunghezza del lato del quadrato.
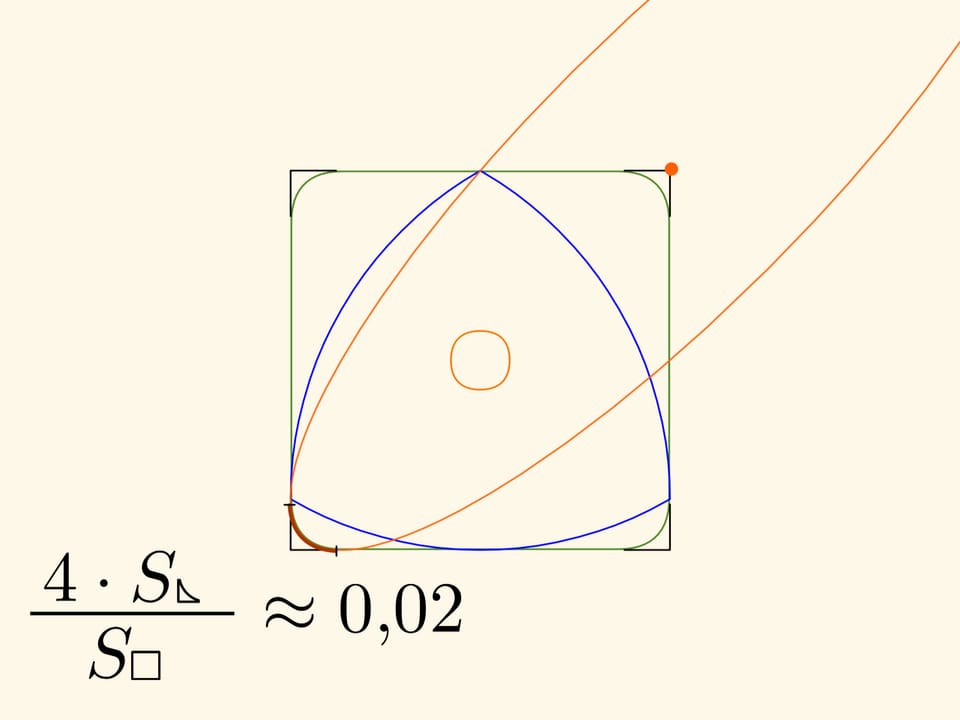
I tratti di curva che rimpiazzano gli angoli retti sono anch’essi degli archi di ellissi, con centri nei vertici del quadrato, con semiassi ruotati di $45^\circ$ rispetto ai lati del quadrato lunghi rispettivamente $k\cdot(\sqrt{3}+1)/2$, $k\cdot(\sqrt{3}-1)/2$.
La superficie del quadrato non inclusa agli angoli risulta essere intorno al 2 percento dell’area dell’intero quadrato!
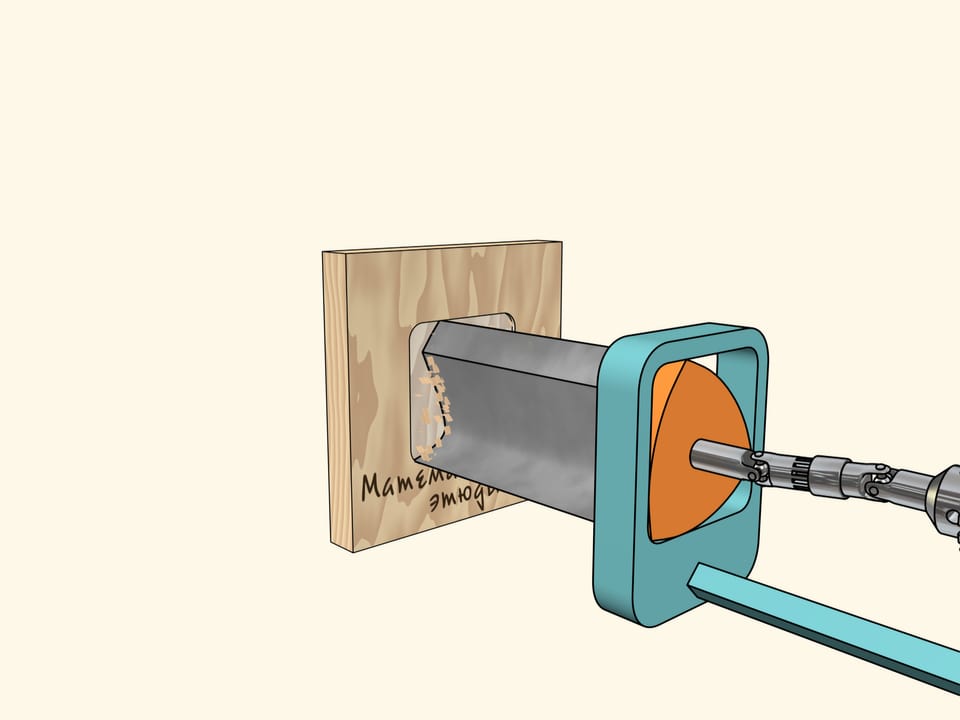
Se ora facciamo la punta di un trapano a forma del triangolo di Reuleaux, allora sarà possibile praticare dei fori quadrati con angoli un po’ arrotondati, ma con i lati assolutamente dritti!
Rimane da costruire un trapano siffatto... O meglio, costruire la punta stessa non è complicato, è sufficiente che abbia sezione simile a un triangolo di Reuleaux, e che i bordi taglienti corrispondano ai vertici del triangolo.
L’unica difficoltà sta nel fatto, come abbiamo già osservato, che la traiettoria del centro del triangolo deve consistere di quattro archi di ellisse. A occhio, questa curva è molto simile a un cerchio, e anche matematicamente è molto vicina ad esso, ma non è un cerchio, mentre qualsiasi eccentrica (ottenuta da un cerchio il cui centro si muove su un altro cerchio di raggio diverso) usata nei meccanismi tecnici, dà un movimento che è rigorosamente circolare.
Nel 1914 l’ingegnere inglese Harry James Watts inventò un modo per superare questa difficoltà. Su una superficie viene ritagliata la sagoma con la forma del quadrato, nella quale si muoverà la punta del trapano. Questa punta è libera di muoversi nel mandrino in modo da coprire tutta l’area all’interno della sagoma. La fabbrica, che ottenne il brevetto di questo meccanismo, iniziò a produrre trapani Watts nel 1916.
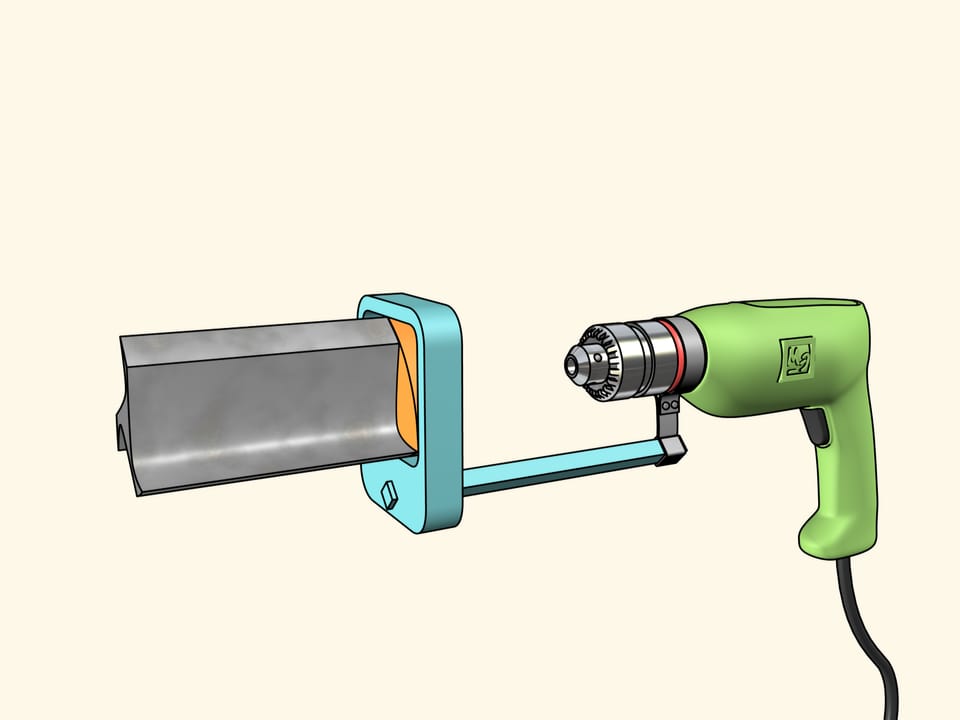
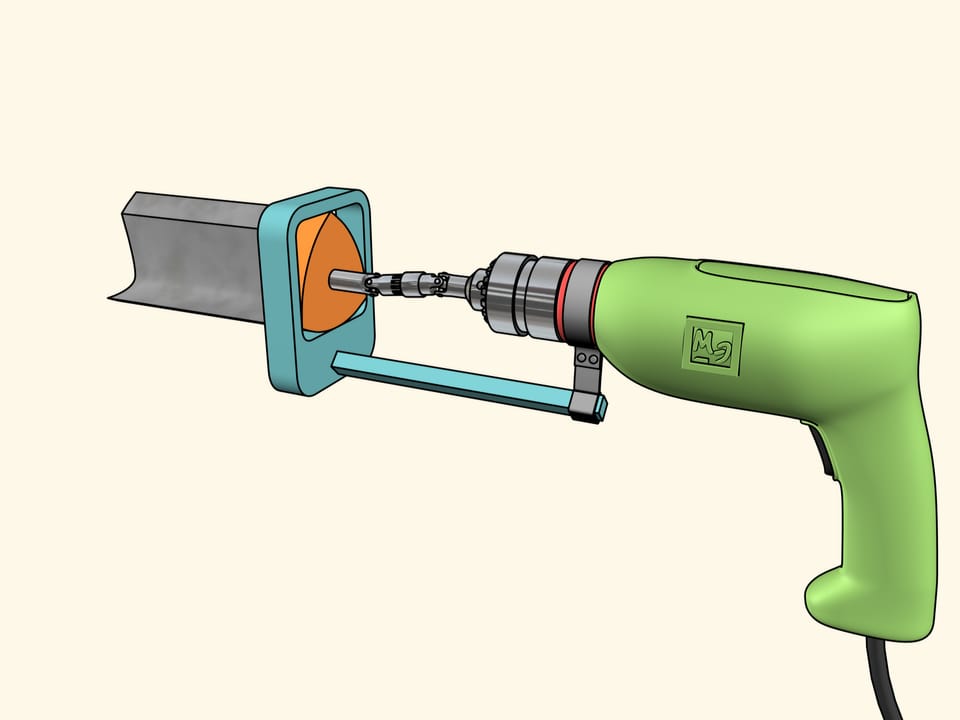
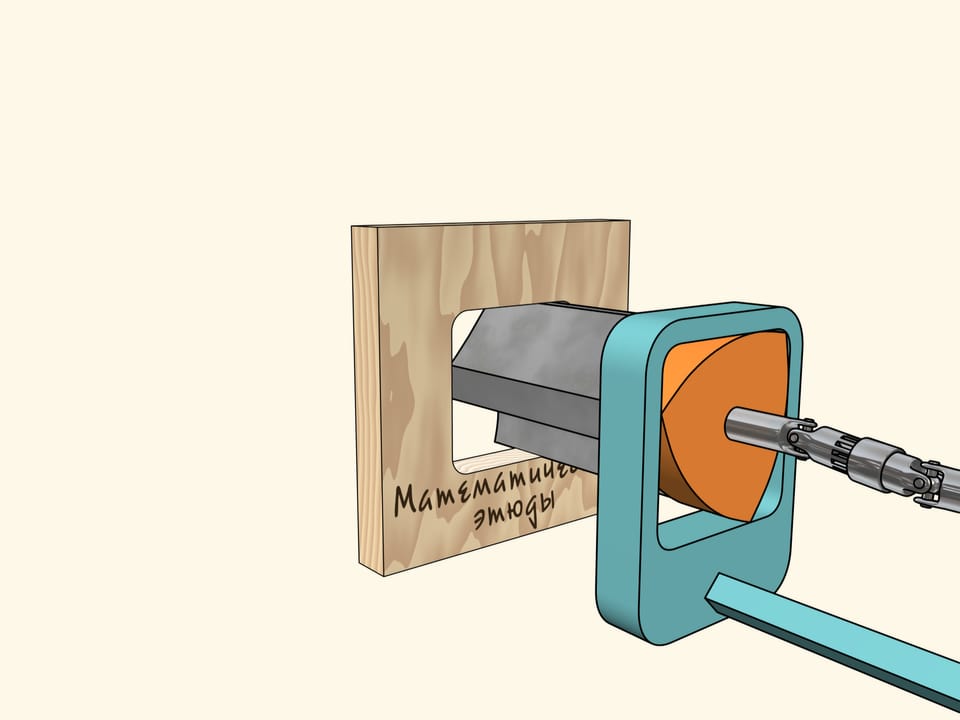
Noi useremo un’altra costruzione. Fissiamo la punta al triangolo di Reuleaux, che si muove in una cornice quadrata che funge da guida. La cornice stessa viene fissata al trapano. Ora non resta che far girare il triangolo di Reuleaux.
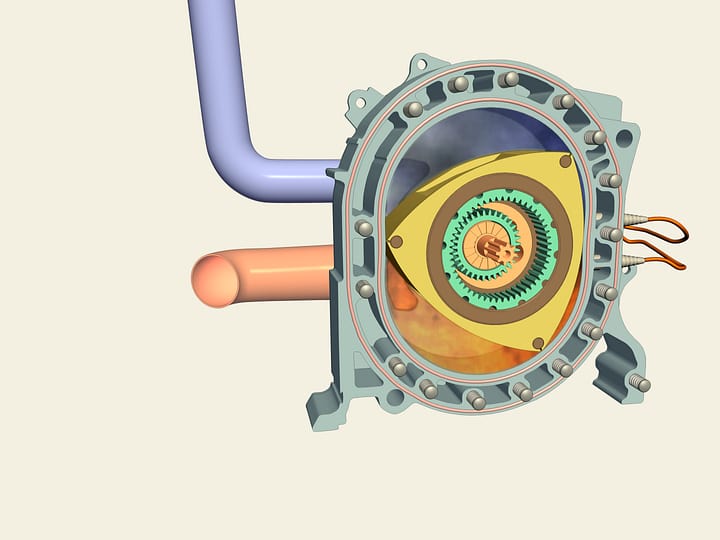
Questo problema tecnico si risolve con l’aiuto di una costruzione che sicuramente avrete visto molte volte, nelle giunzioni che connettono un autocarro al rimorchio. Si tratta del giunto cardanico. Questo giunto prende il nome da l suo inventore, Gerolamo Cardano.
Gerolamo Cardano 1501—1576
Quando nel 1541 l’imperatore Carlo V entrò trionfalmente in Milano, appena conquistata, Cardano, rettore del Collegio dei Medici, gli stava vicino sotto un baldacchino. In ringraziamento per quell’onore propose di modificare il traino della carrozza imperiale per mezzo di due giunti, la cui rotazione permetteva alla carrozza di mantenere la posizione orizzontale [...]
Onestamente bisogna notare che l’idea di un simile meccanismo risale all’antichità, e che già nel “Codice Atlantico” di Leonardo da Vinci c’è il disegno di una bussola per una nave con sospensione cardanica. Tali bussole furono adottate nella prima metà del XVI secolo, probabilmente, indipendentemente da Cardano.
S. G. Gindikin, Racconti di Fisica e Matematica.
Ora tutto è pronto per la foratura. Prendiamo un foglio di compensato e facciamo un foro quadrato! Come abbiamo già detto, i lati saranno perfettamente rettilinei, e soltanto gli angoli saranno un po’ smussati. Se necessario, possiamo correggerli con una lima.