Dopo la guerra, nel 1947, furono introdotte in Unione Sovietica delle nuove banconote, che erano ancora in circolazione nel 1956.
In quell’anno Vladimir Igorevich Arnold pose il problema del rublo ripiegato. Si può costruire un poligono planare ripiegando un foglio di carta (una banconota da un rublo) in modo che il perimetro di questo poligono sia più grande del perimetro del foglio originale?
Nel 1961 in Russia cambiarono di nuovo le monete e le banconote, sicché cambiò anche il disegno del rublo, che diventò un foglio di carta molto più piccolo. A quell’epoca comunque il problema non era ancora stato risolto.
Osserviamo che, sebbene una risposta positiva “è possibile” contraddica l’intuizione, ci deve essere una ragione matematica per una risposta negativa. Se si piega un rettangolo lungo una linea retta, allora il perimetro può solo ridursi: al bordo già esistente si deve aggiungere il segmento di quella retta lungo la quale si è fatta la piega, ma bisogna togliere una linea spezzata che ha gli stessi estremi di quel segmento. Se si fa un’operazione simile, ossia si piega lungo una retta il poligono ottenuto, la situazione sarà la stessa: il perimetro aumenta della lunghezza di un segmento, ma diminuisce della lunghezza di una spezzata. Questo tipo di piegatura – lungo una retta – viene detto “semplice” e può sempre solo diminuire il perimetro. Questa tuttavia è soltanto una ragione, ma non è ancora una dimostrazione.
Sicché si può o no aumentare il perimetro del rettangolo iniziale? Negli anni 1991 e 1993 vennero cambiate un’altra volta le banconote, e quella del rublo del ’61 uscì di circolazione. Ma il problema di Arnold restava ancora irrisolto.
Da quell’epoca un rublo russo vale, purtroppo, così poco che non esistono più banconote, ma solo monete, di quel valore.
All’inizio del XXI secolo tuttavia il problema fu risolto. La prima soluzione matematicamente rigorosa la diede un allievo di N.P. Dolbilin, Aleksej Tarasov. Egli inventò un algoritmo per ripiegare un quadrato in modo che in totale si ottenga un poligono planare con un perimetro maggiore.
Coloro che desiderano solo godersi il film, possono saltare la parte seguente, che invece aggiungiamo per coloro che desiderano capire per bene come va piegato il foglio.
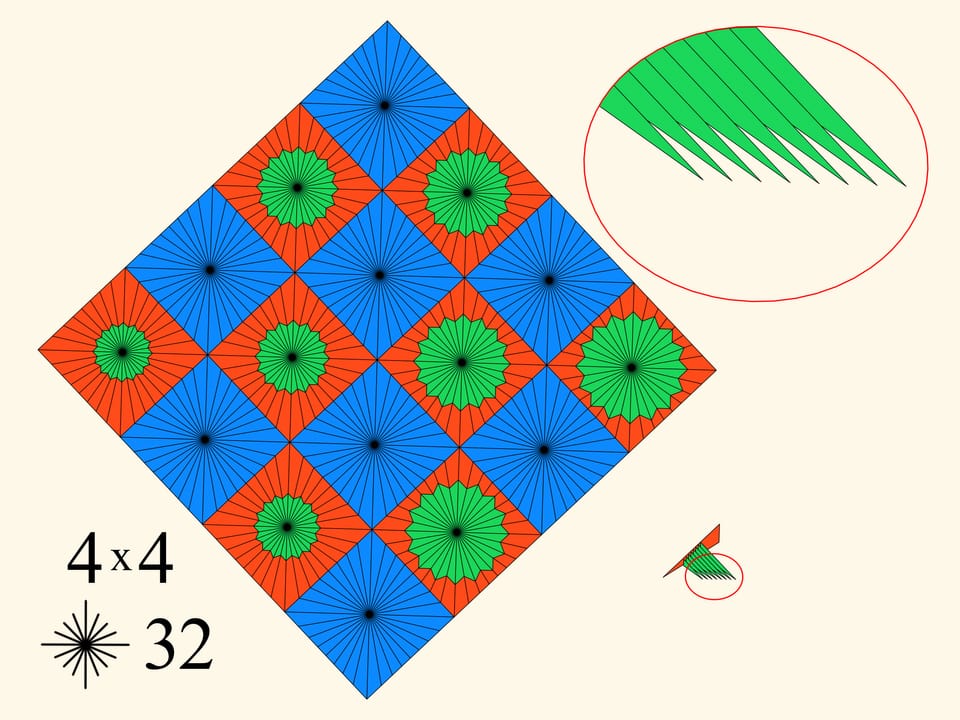
Prendiamo un foglio di carta quadrato e dividiamolo in celle quadrate, per esempio, 4 x 4. Coloriamo le celle con due colori come una scacchiera e in ogni quadrato tracciamo dal centro un numero definito di raggi. Aggiungiamo poi nei quadrati rossi delle stelle verdi, in modo che le loro dimensioni crescano nella direzione di una diagonale. Ora ripieghiamo il foglio di carta in una striscia, e quindi in un rettangolo, e, alla fine, in un triangolo. L’oggetto ottenuto è fatto nel modo seguente. Contiene diversi strati azzurri in una delle sue metà, e in quell’altra strati rossi. Il modo di tracciare le stelle verdi è stato tale che dopo il ripiegamento esse aumentano di dimensione man mano che si passa da uno strato all’altro nella sezione del triangolo, come se fossero una dentro l’altra. Incominciamo quindi a ripiegare il triangolo in modo che gli strati blu vengano fuori parallelamente da una parte, e quelli verdi e rossi dall’altra. Si ottiene una superficie che, alla fine, si ripiega ancora in un poligono planare.
Questo poligono ha una parte rossa (i triangoli blu si trovano all’interno dell’oggetto ripiegato) e un pettine verde. Osserviamo che il pettine ha tanti denti quante erano le stelle verdi, cioè i quadrati rossi.
Ma è cresciuto il perimetro rispetto al quadrato iniziale? È stato risolto il problema? Se si paragonano le figure, si vede subito che il perimetro è diminuito. Perché allora si è fatta questa piegatura tanto complicata?
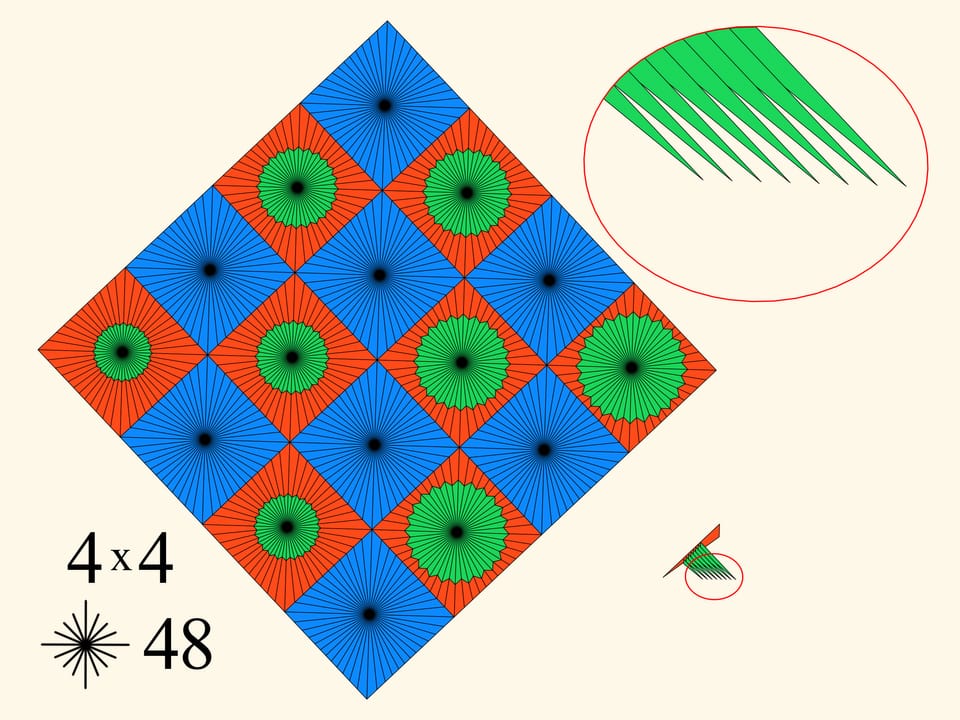
Nell’esempio concreto abbiamo impiegato un algoritmo generale. E in questo algoritmo ci sono due parametri: il numero delle celle in cui è suddiviso il quadrato iniziale e il numero dei raggi in ogni quadrato. Osserviamo cosa succede se cambiamo questi parametri.
Per la stessa suddivisione 4x4 aumenteremo il numero dei raggi dentro ogni cella. Questo porta a un assottigliamento dei denti del pettine, a una minore intersezione di essi, e di conseguenza, a una modesta crescita del perimetro.
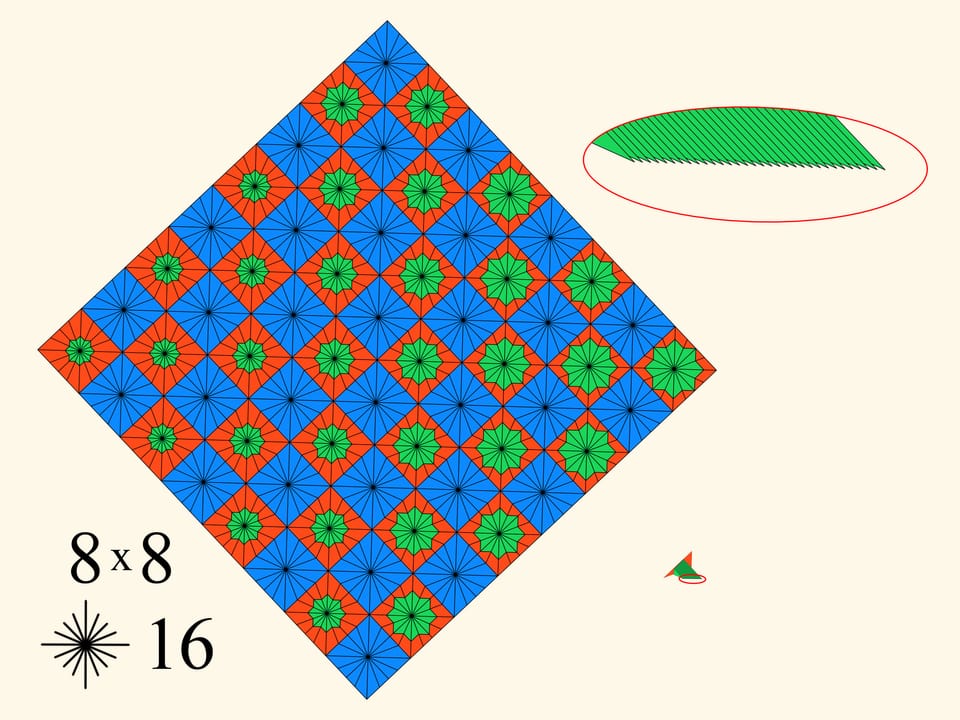
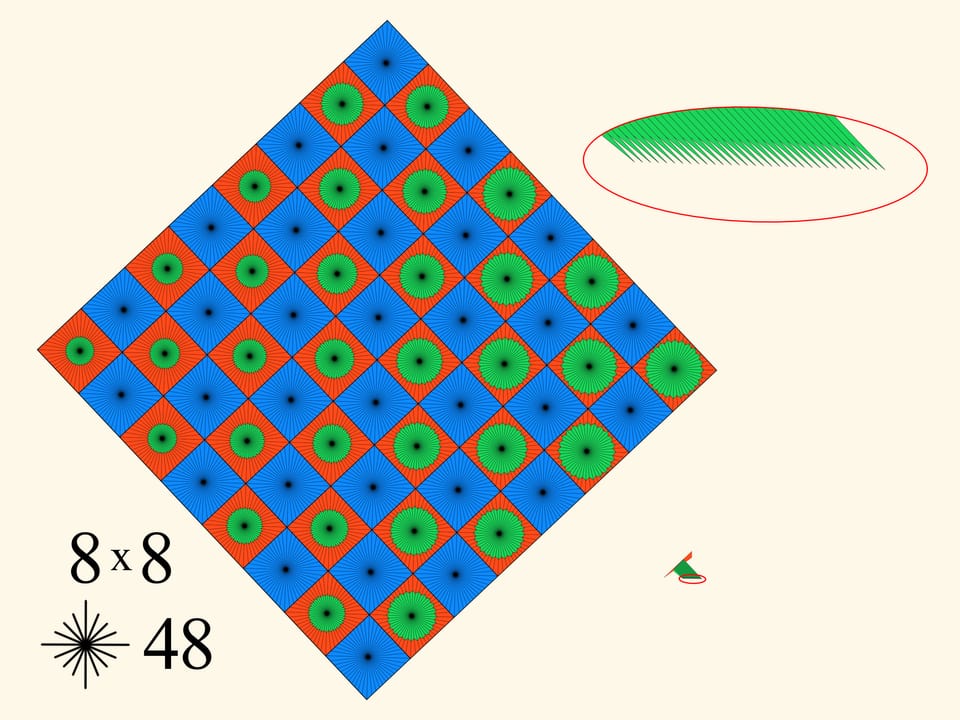
C’è ancora un altro parametro, la quantità di celle in cui si è suddiviso il quadrato iniziale. Se si aumenta questo parametro, allora nella costruzione aumenta il numero di denti del pettine.
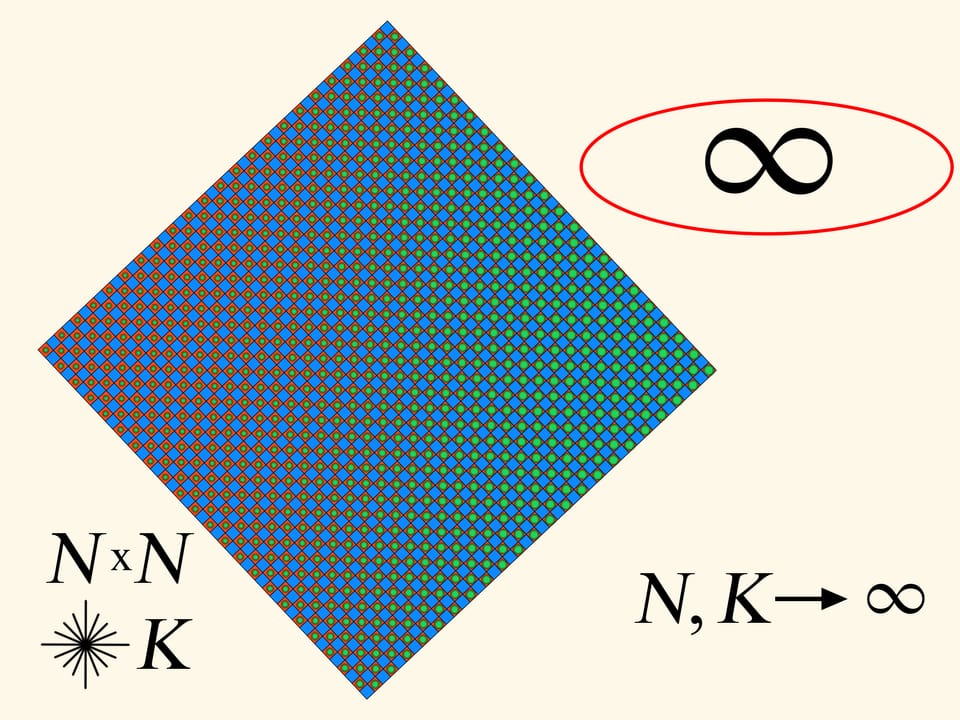
L’aumento contemporaneo dei due parametri –– sia del numero di celle, sia della quantità di raggi – dà un aumento del perimetro. Ma di quanto può aumentare? Si trova, fino all’infinito. Ma questo significa che ad un certo momento esso supererà il perimetro del quadrato iniziale!
Il problema del rublo ripiegato – ripiegare un rettangolo e aumentarne il perimetro – è risolto. Ma quante volte bisognerà fare delle pieghe? Piuttosto tante. Dal lavoro di A. Tarasov si può ottenere una stima: per una suddivisione in 16x16 celle e un numero di raggi in ogni cella di 16²•30 il perimetro del poligono ottenuto sarà più grande del perimetro del quadrato iniziale.
Nel film questo non si può mostrare, ma si può realizzare nella realtà? Sicuramente ricordate bene che piegare un foglio di carta, sia pure molto sottile, si può per non più di 7–8 volte. Se non fate questo da molto tempo, provateci con un semplice esperimento. Sicché che cosa offre allora il problema stesso, posto da V.I. Arnold, e tale soluzione con un algoritmo “non realizzabile”? Certamente uno strumento di avanzamento nella scienza, che senza dubbio tornerà utile in uno sviluppo futuro.