Ricordate che forma aveva un pacchetto di latte cinquanta anni fa? È sorprendente che tutta l’Italia comprasse dei pacchetti simili quasi ogni giorno, per più di venti anni, ma pochi ora ricordano precisamente cosa ci fosse scritto sopra. Lo steso avviene per tutta la Russia!
Ma tutti ovviamente ricordano che il pacchetto di latte aveva la forma di un tetraedro (una piramide triangolare regolare). I pacchetti a forma di tetraedro furono inventati dalla fabbrica Tetra Pak negli anni 40 del XX secolo, che da essi stessi prese il nome. Le innovazioni apportate a quei tempi dalla TetraPak erano due. In primo luogo, per la prima volta liquidi alimentari furono messi in imballaggi di cartone. In secondo luogo, la produzione degli imballaggi tetraedrici era così facile che ne fu possibile la fabbricazione direttamente presso le fabbriche di latte.
Il pacchetto di latte più comune in Unione Sovietica era questo.
Ma è possibile ripiegare il pezzo di cartone di cui è fatto un pacchetto di latte in modo da ottenere un pacchetto più capiente?
Matematicamente parlando, è possibile ripiegare lo sviluppo di un tetraedro in un poliedro con un volume maggiore?
Un teorema di A. Aleksandrov dice che non è possibile ripiegarlo in un poliedro convesso con maggiore volume. Tuttavia, potrebbe essere possibile ottenere un poliedro non convesso con maggiore volume.
Per quanto strano possa sembrare, è possibile!
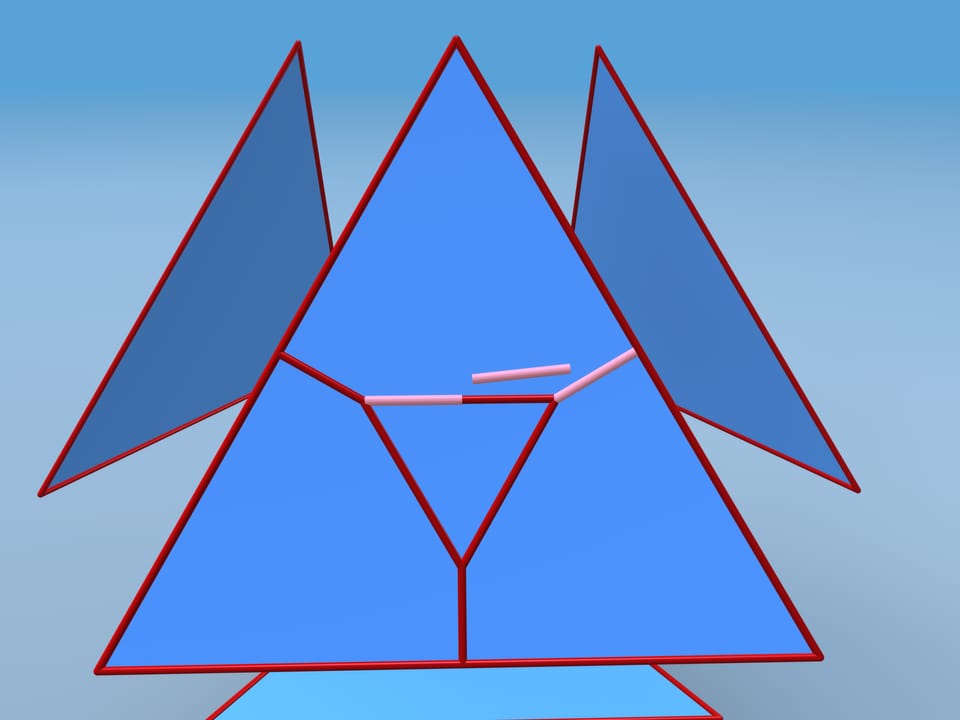
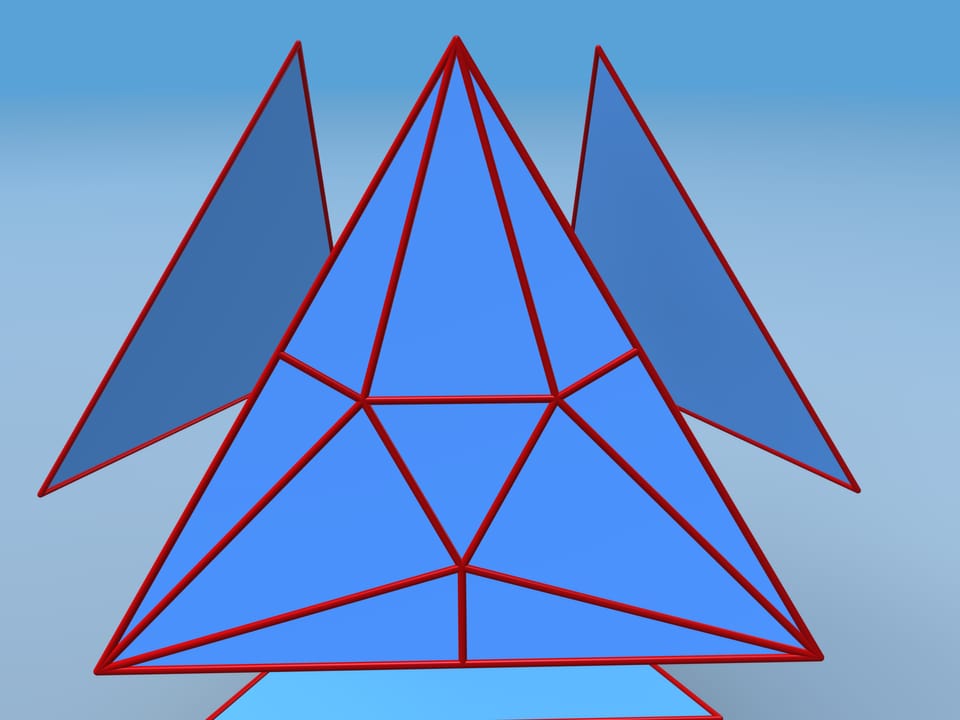
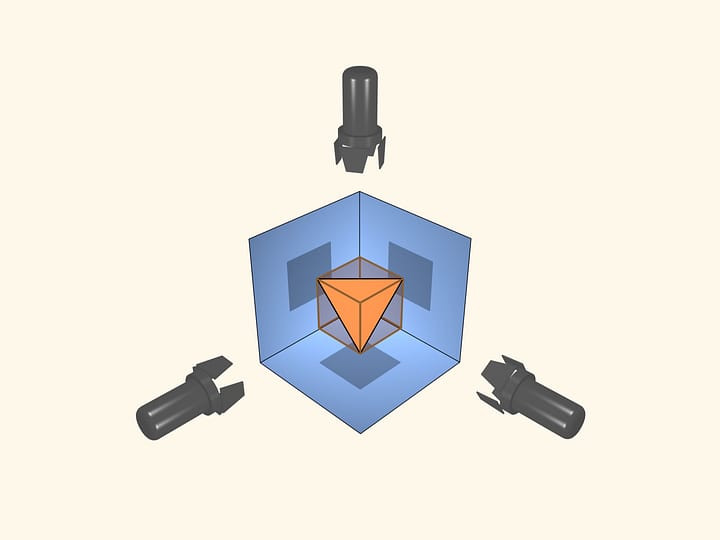
Seguiamo la costruzione che David D. Bleecker ha suggerito nel 1996. Allontaniamo l’una dall’altra le facce e aggiungiamo nuovi vertici e spigoli nel modo seguente. Al centro di ogni faccia consideriamo un triangolo equilatero col lato lungo il doppio della distanza tra il suo vertice e lato della faccia. Tracciamo gli spigoli aggiuntivi.
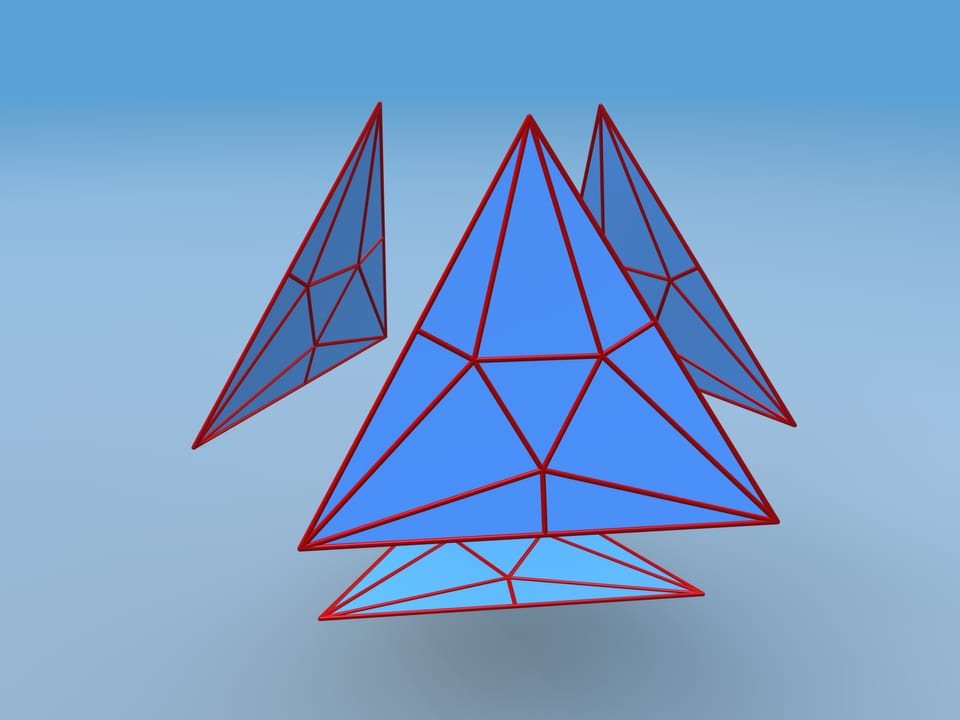
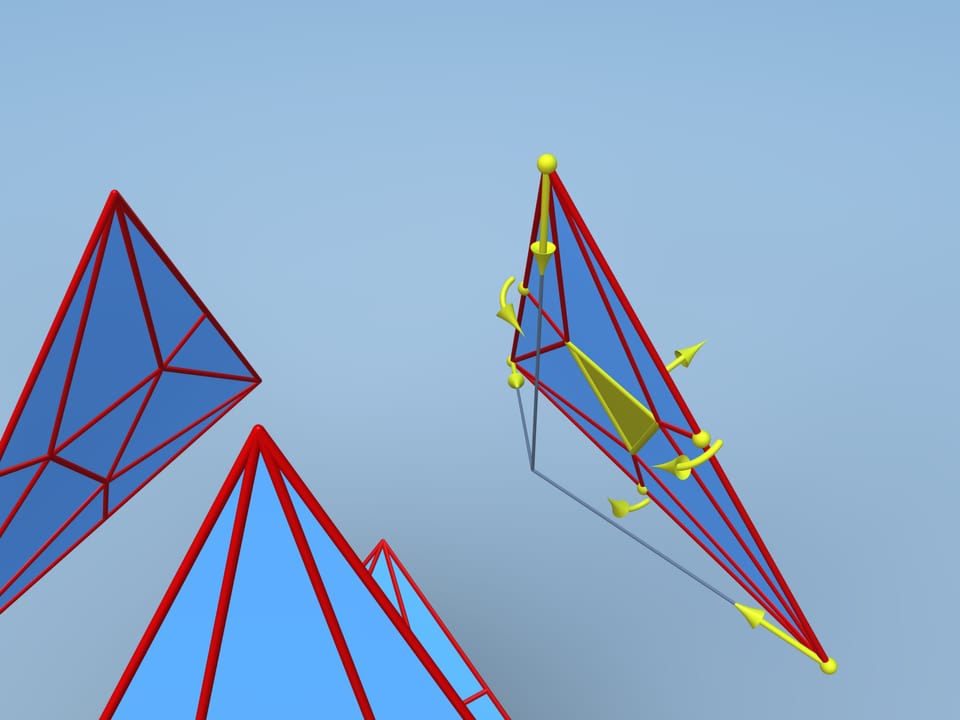
Ripetiamo la stessa procedura su ogni faccia. Ripieghiamo ogni faccia lungo gli spigoli in modo che i suoi vertici e i punti medi dei lati muovano verso il centro del tetraedro, mentre il triangolo al centro ne resti lontano. Riincolliamo le quattro parti. Alcune delle nuove facce risultano complanari per cui gli spigoli che le separano scompaiono.
Per calcolare il volume di questo poliedro, lo divideremo in pezzi. Il nostro poliedro è costituito di quattro piramidi esagonali tutte uguali e di un tetraedro troncato ai vertici. Per semplificare il calcolo, attaccheremo piccoli tetraedri al nostro tetraedro troncato e quindi sottrarremo il loro volume dal volume del tetraedro intero.
Scopriamo così che il volume del poliedro è del 37,7% superiore a quello del poliedro iniziale. Quindi, il pezzo di cartone con cui è stato fatto il pacchetto tetraedrico può essere ripiegato in un pacchetto più di un terzo più capiente!
Sorprendentemente, il tetraedro non è un’eccezione. Si è scoperto che lo sviluppo di qualsiasi poliedro convesso con facce triangolari può essere ripiegato in un poliedro con maggiore volume. Questo teorema è stato dimostrato da D. Bleeker nel 1996, che ha pure proposto un algoritmo per farlo.
Nel suo articolo, D. Bleecker considera, oltre poliedri con facce triangolari, due poliedri che non appartengono a questa classe: il cubo e il dodecaedro. Anche i loro sviluppi possono essere ripiegati in poliedri non convessi che racchiudono più volume rispetto a quelli iniziali.
Congettura
Lo sviluppo di qualsiasi poliedro convesso può essere ripiegato in modo da ottenere un poliedro non convesso con maggiore volume.
Problemi aperti
Dimostrare (o confutare) la congettura.
Quanto può essere grande al massimo il volume del poliedro ottenuto dal ripiegamento dello sviluppo di un tetraedro?