Нахождение соотношения между объёмами шара и описанного около него цилиндра Архимед (Архимед Сиракузский, др.-греч. Ἀρχιμήδης, лат. Archimedes, 287 до н. э. — 212 до н. э.) считал своим главнейшим математическим открытием. Не случайно на надгробии Архимеда были изображены шар и цилиндр.
Архимед Досифея приветствует! Незадолго перед сим я препроводил к тебе некоторые предметы моих иcследований, вместе с найденными мною доказательствами […] Ныне я кончил и другие некоторые мне на мысль пришедшие теоремы, из коих достопримечательнейшие суть сии: […] Цилиндр, имеющий основанием наибольший круг шара, а высоту, равную поперечнику оного, есть полуторный шара; и его поверхность есть полуторная же поверхности шара. Свойства сии без сомнения существовали в сказанных фигурах, но доселе не были ещё замечены никем из занимавшихся Геометрией.
Архимед. О шаре и цилиндре
Когда я был квестором, я отыскал в Сиракузах его <Архимеда> могилу, со всех сторон заросшую терновником, словно изгородью, потому что сиракузяне совсем забыли о ней, словно ее и нет. Я знал несколько стишков, сочиненных для его надгробного памятника, где упоминается, что на вершине его поставлены шар и цилиндр. И вот, осматривая местность близ Акрагантских ворот, где очень много гробниц и могил, я приметил маленькую колонну, чуть–чуть возвышавшуюся из зарослей, на которой были очертания шара и цилиндра. Тотчас я сказал сиракузянам — со мной были первейшие граждане города, — что этого–то, видимо, я и ищу. Они послали косарей и расчистили место. Когда доступ к нему открылся, мы подошли к основанию памятника. Там была и надпись, но концы её строчек стёрлись от времени почти наполовину. Вот до какой степени славнейший, а некогда и учёнейший греческий город позабыл памятник умнейшему из своих граждан: понадобился человек из Арпина, чтобы напомнить о нём.
Цицерон о могиле Архимеда в сочинении «Тускуланские беседы». Перевод М. Гаспарова.
(Цит. по: Цицерон Марк Туллий. Избранные сочинения. Пер. с латин. — М. : Худ. лит., 1975. — С. 342)
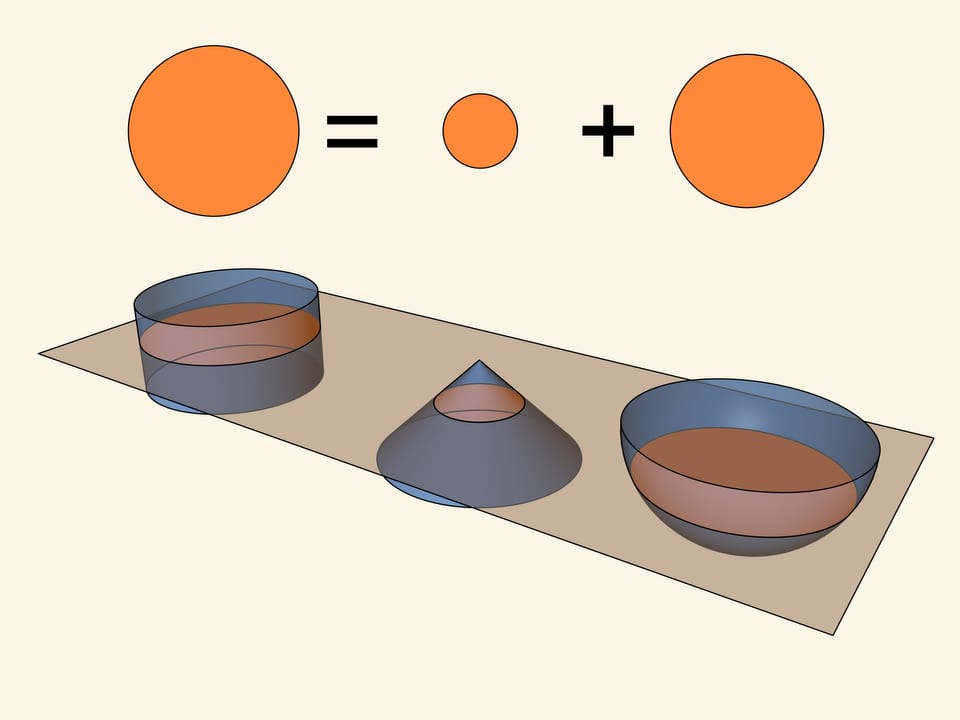
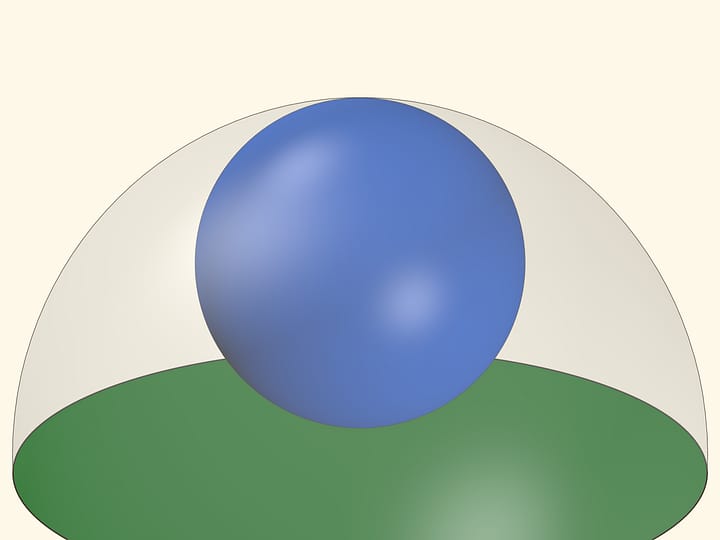
Рассмотрим рычажные весы. Представим, что с одной стороны весов расположен цилиндр, высотой равной радиусу основания, а с другой стороны, на том же расстоянии от подвеса что и цилиндр, — конус и половина шара. Причём такие, что радиус основания конуса и высота равны радиусу цилиндра, радиус шара равен радиусу цилиндра.
Начнём послойно набирать эти фигуры так, чтобы высоты слоёв каждой из трёх фигур были одинаковы. Оказывается, при указанных соотношениях рычажные весы всегда будут приходить в равновесие. Когда фигуры будут полностью собраны, весы будут находиться в равновесии. Значит, объём цилиндра равен сумме объёмов конуса и половины шара, если радиусы и высоты всех трёх фигур совпадают.
Удивительно: с одной стороны весов простая фигура — прямой круговой цилиндр, с другой стороны одна из фигур тоже относительно простая — прямой круговой конус, а уравновешивающая весы фигура — шар.
Дело в том, что если провести плоскость, параллельную основаниям фигур, то площадь круга, получающегося в сечении цилиндра равна сумме площадей кругов, получающихся в сечении рассматриваемых конуса и шара. Несложно (в наше время!) прямым вычислением проверить, что равенство площадей будет выполняться для любого положения секущей плоскости.
Из указанного равенства площадей, как сейчас говорят, по принципу Кавальери (итал. Bonaventura Francesco Cavalieri, лат. Cavalerius, 1598—1647), следует равенство объёмов.
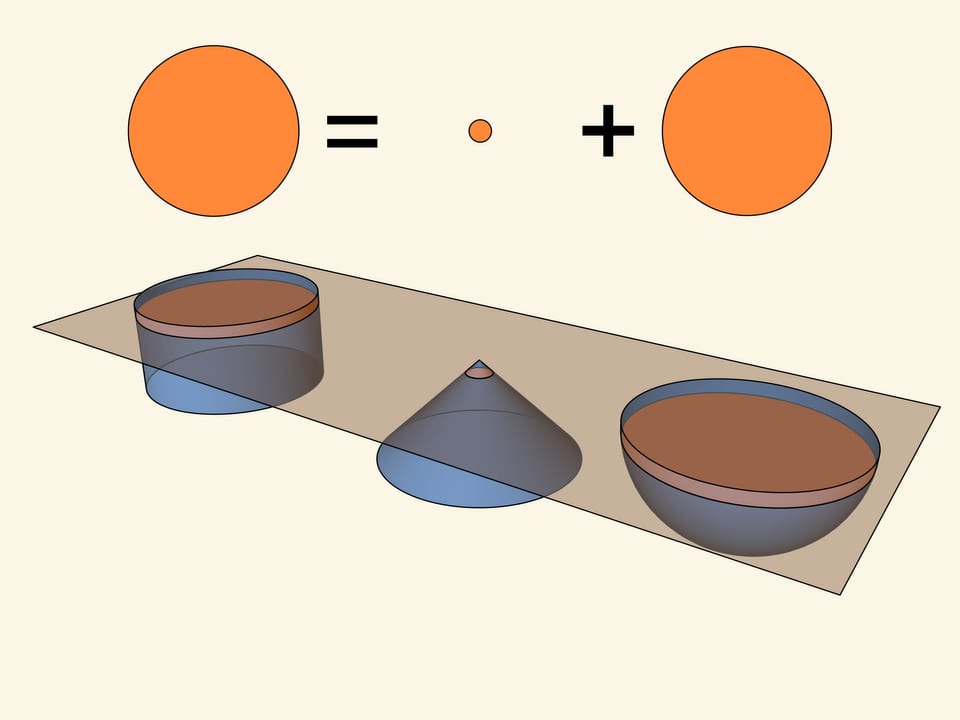
Отношение объёмов цилиндра и конуса было известно до Архимеда:
Таким образом и Евдокс <Евдокс Книдский, др.-греч. Εὔδοξος, лат. Eudoxus, ок. 408 до н. э. — ок. 355 до н. э.> собственным рассуждением открыл многое о телах, например: что всякая пирамида есть треть призмы, имеющей с пирамидой то же основание и ту же высоту; что всякий конус есть треть цилиндра, имеющего с конусом то же основание и ту же высоту.
Архимед. О шаре и цилиндре
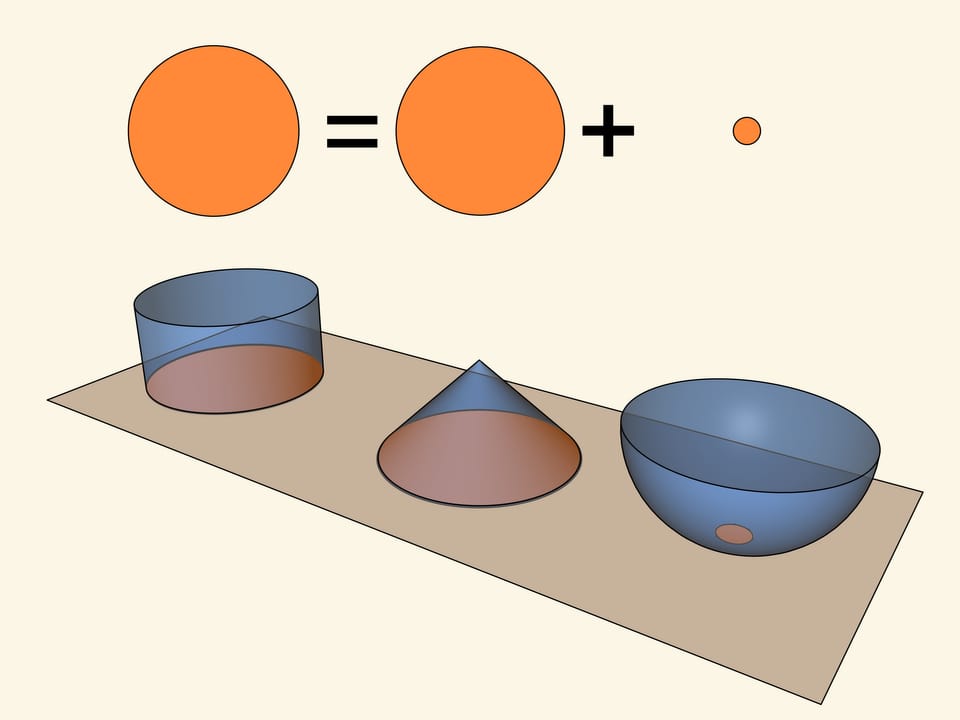
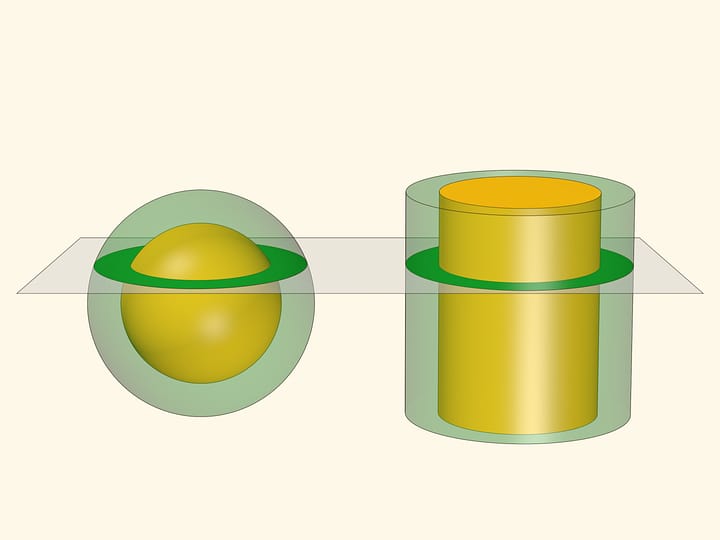
Равновесие весов даёт возможность выразить объём половины шара через объём цилиндра. Вычитая из объёма цилиндра треть — объём конуса с теми же основанием и высотой, что и у цилиндра, — получаем, что объём половины шара равен $2/3$ от объёма цилиндра.
Тем самым, установлено соотношение, описанное у Архимеда: объём шара, равен $2/3$ объёма описанного около шара цилиндра. Интересно, что, как заметил Архимед, в том же отношении находятся и площади их поверхностей.
Из соотношения Архимеда можно вывести явную формулу для объёма шара. В случае цилиндра, описанного вокруг шара радиуса $R$, площадь его основания равна $\pi R^2$, а высота равна $2R$. Значит объём цилиндра равен: $(\pi R^2)\cdot (2 R)=2 \pi R^3$. Умножив на коэффициент $2/3$, получим формулу для объёма шара: $4/3 \cdot \pi R^3$.
Впрочем, оставляя всё сие на уважение людей, могущих судить о таковых вещах, я с моей стороны желал бы выдать в свет сие сочинение при жизни ещё Конона <Конон Самосский, др.-греч. Κόνων, лат. Conon, ок. 280 до н.э. — ок. 220 до н. э.>, который весьма мог вникнуть в оное, и назначить всему настоящую цену. Как бы то ни было, полагая что и другим занимающимся математическими науками не бесполезно будет знать мои теоремы, я посылаю оные к тебе с надлежащими доказательствами, дабы знающие сей предмет, рассмотрели оные.
Архимед. О шаре и цилиндре
Литература
Архимед. О шаре и цилиндре. Книга I // Архимеда две книги о шаре и цилиндре, измерение круга и леммы / Пер. с греч. и лат. Ф. Петрушевского. — СПб., 1823.
Архимед. Сочинения / Перевод, вступительная статья и комментарии И. Н. Веселовского. — М. : ГИФМЛ, 1962.
Цицерон Марк Тулий. Тускуланские беседы // Цицерон Марк Туллий. Избранные сочинения / Пер. с лат. М. Гаспарова. — М. : Художественная литература, 1975. — С. 342.