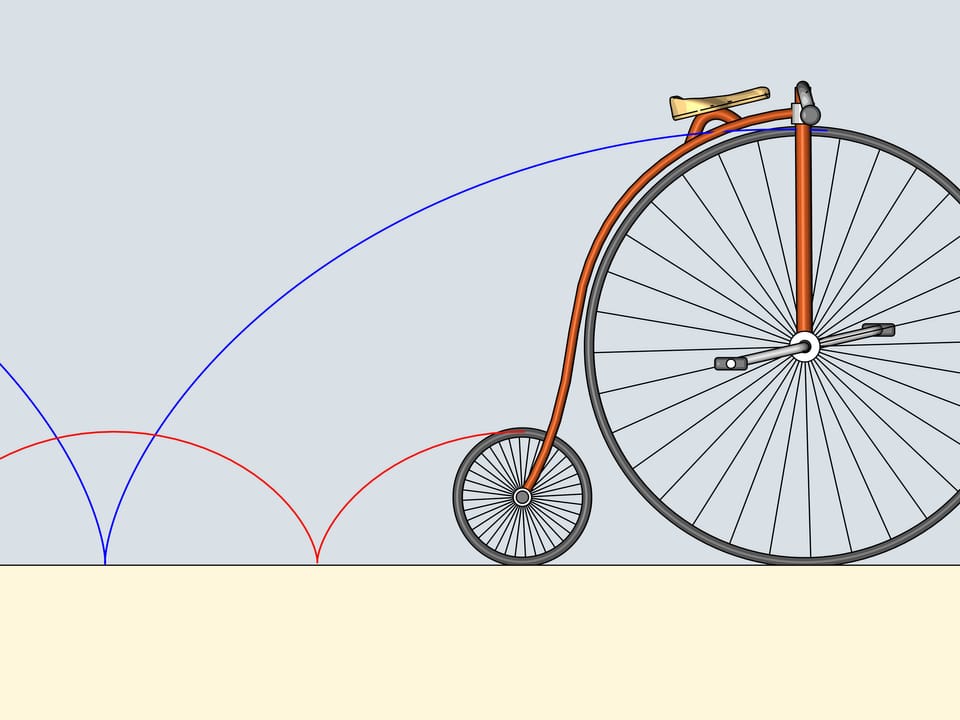
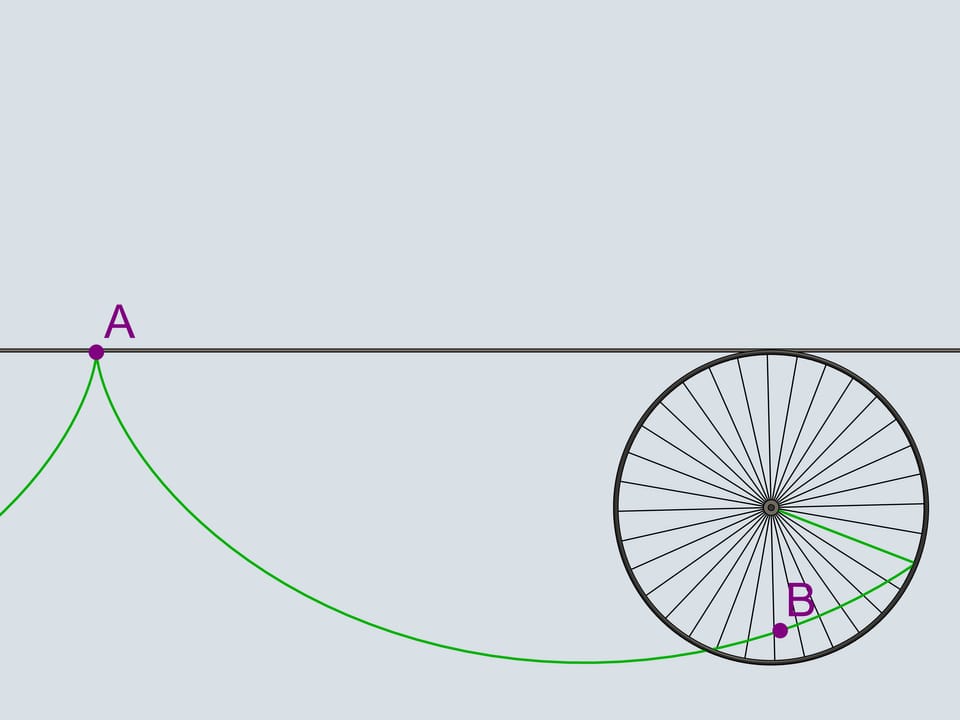
Помните оранжевые пластмассовые катафоты — светоотражатели, прикрепляющиеся к спицам велосипедного колеса? Прикрепим катафот к самому ободу колеса и проследим за его траекторией. Полученные кривые принадлежат семейству циклоид.
Колесо при этом называется производящим кругом (или окружностью) циклоиды.
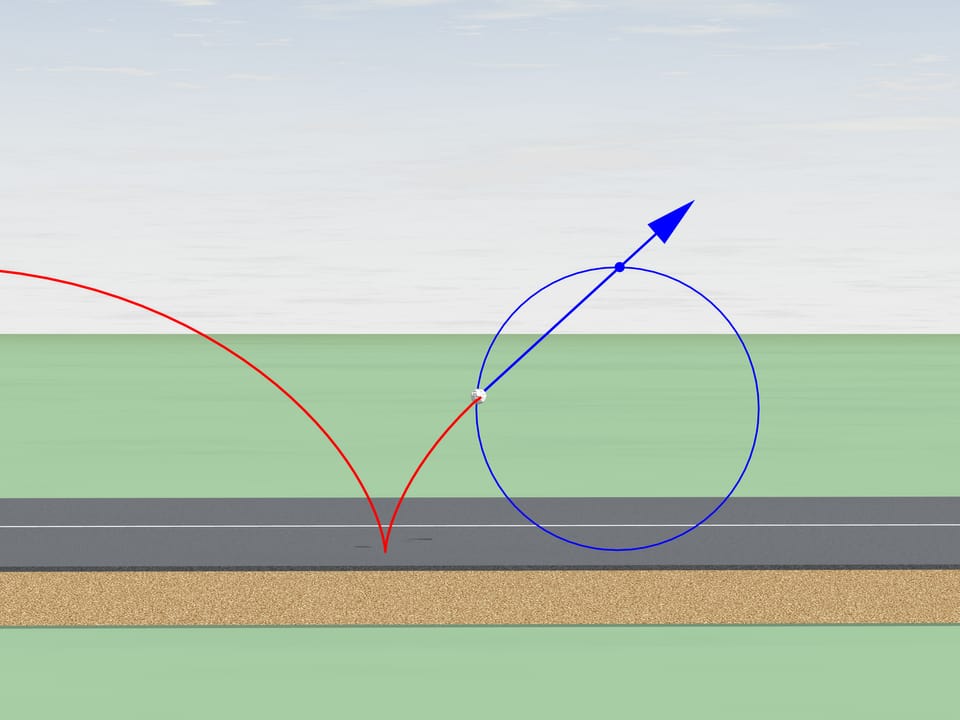
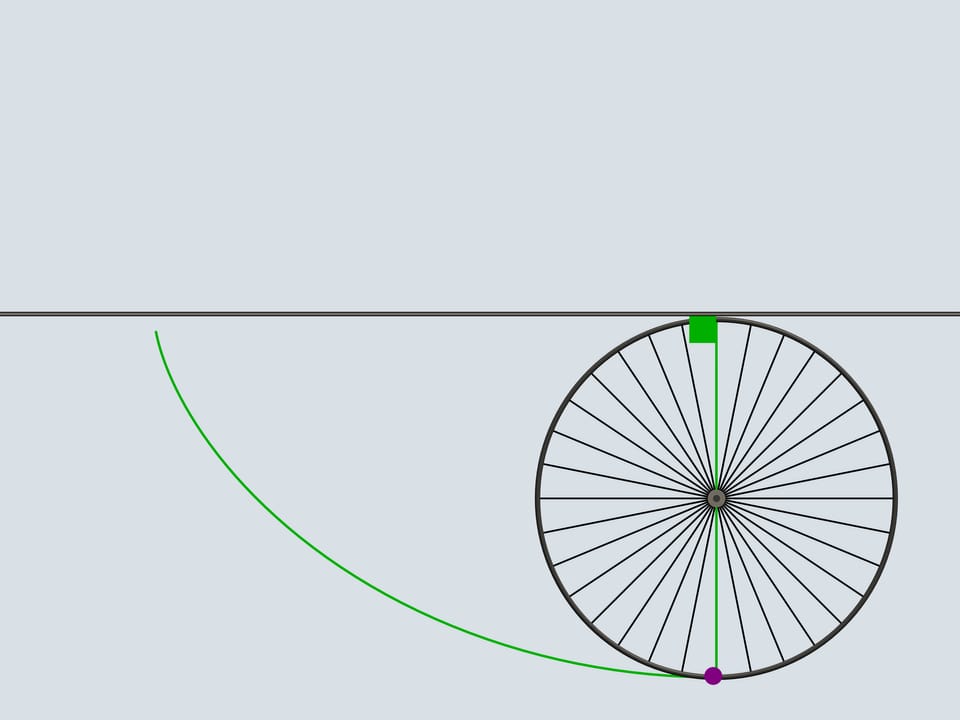
Но давайте вернёмся в наш век и пересядем на более современную технику. На пути байка попался камушек, который застрял в протекторе колеса. Провернувшись несколько кругов с колесом, куда полетит камень, когда выскочит из протектора? Против направления движения мотоцикла или по направлению?
Как известно, свободное движение тела начинается по касательной к той траектории, по которой оно двигалось. Касательная к циклоиде всегда направлена по направлению движения и проходит через верхнюю точку производящей окружности. По направлению движения полетит и наш камушек.
Помните, как Вы катались в детстве по лужам на велосипеде без заднего крыла? Мокрая полоска на вашей спине является житейским подтверждением только что полученного результата.
Век XVII — это век циклоиды. Лучшие учёные изучали её удивительные свойства.
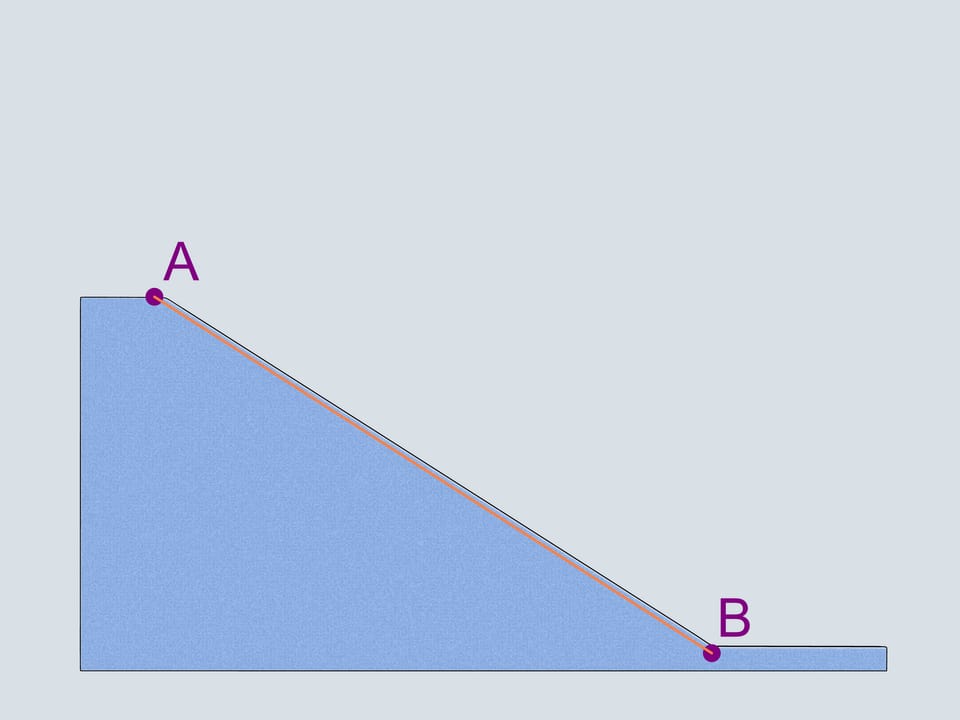
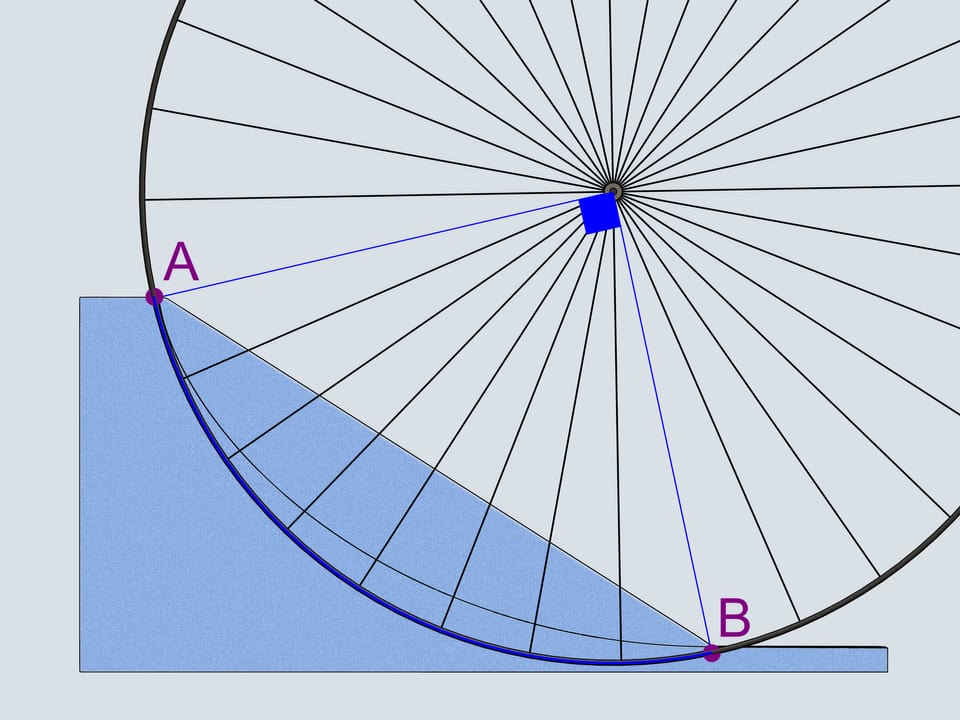
Какая траектория приведёт тело, движущееся под действием силы тяжести, из одной точки в другую за кратчайшее время? Это была одна из первых задач той науки, которая сейчас носит название вариационное исчисление.
Минимизировать (или максимизировать) можно разные вещи — длину пути, скорость, время. В задаче о брахистохроне минимизируется именно время (что подчёркивается самим названием: греч. βράχιστος — наименьший, χρόνος — время).
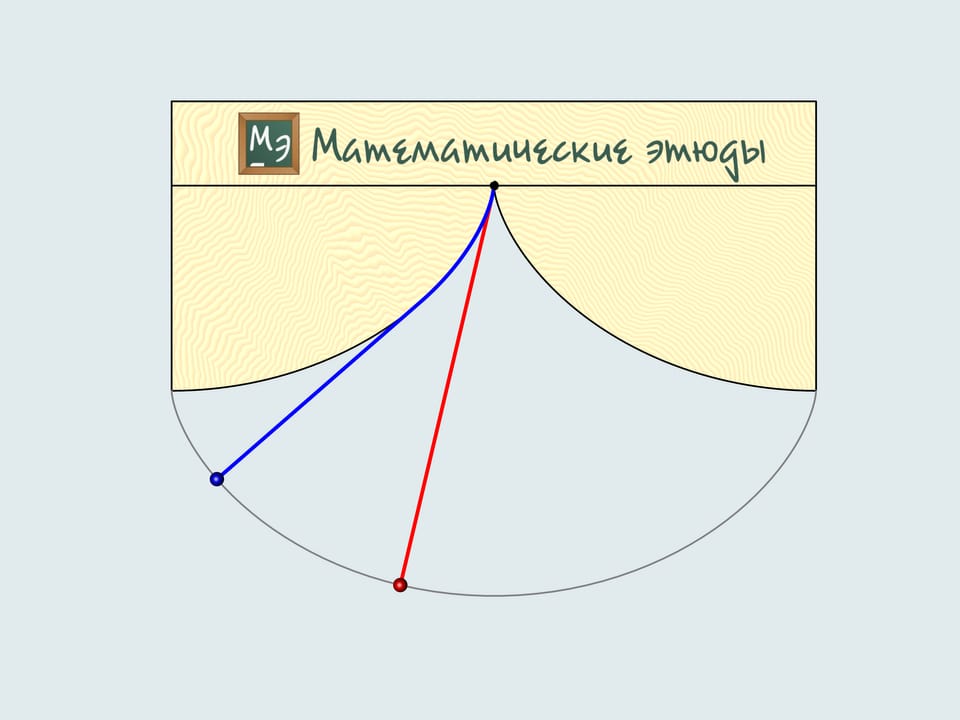
Первое, что приходит на ум, — это прямолинейная траектория. Давайте также рассмотрим перевёрнутую циклоиду с точкой возврата в верхней из заданных точек. И, следуя за Галилео Галилеем, — четвертинку окружности, соединяющую наши точки.
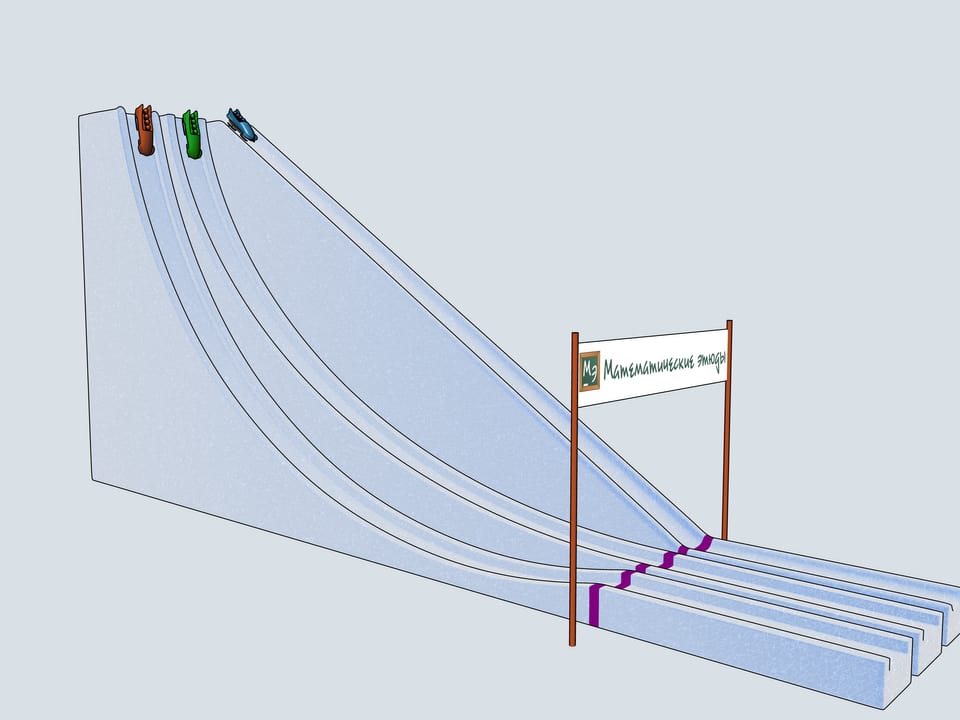
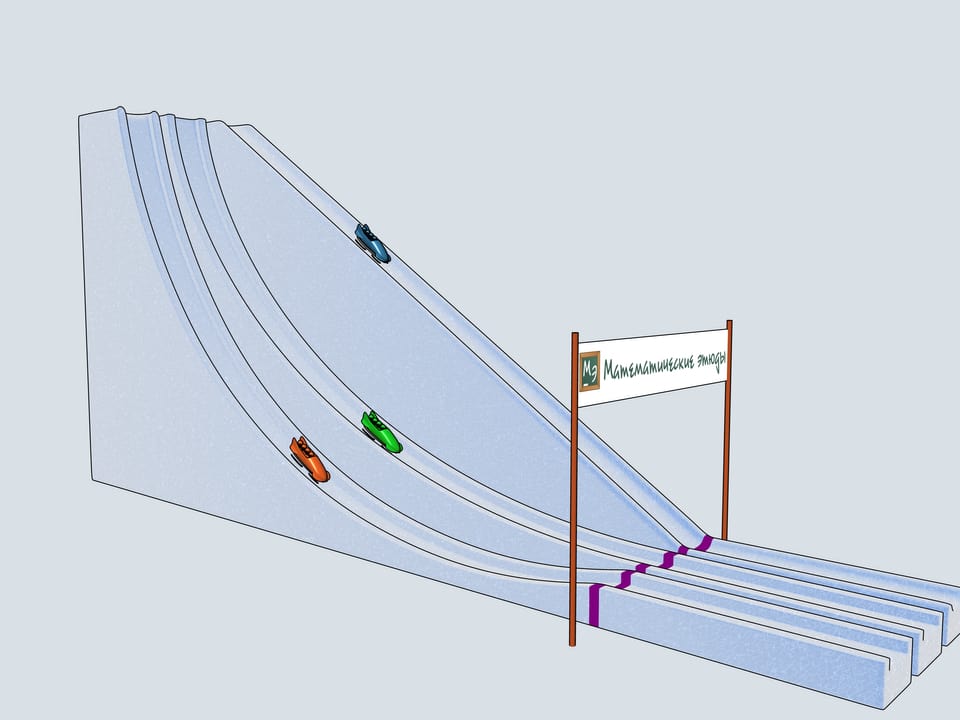
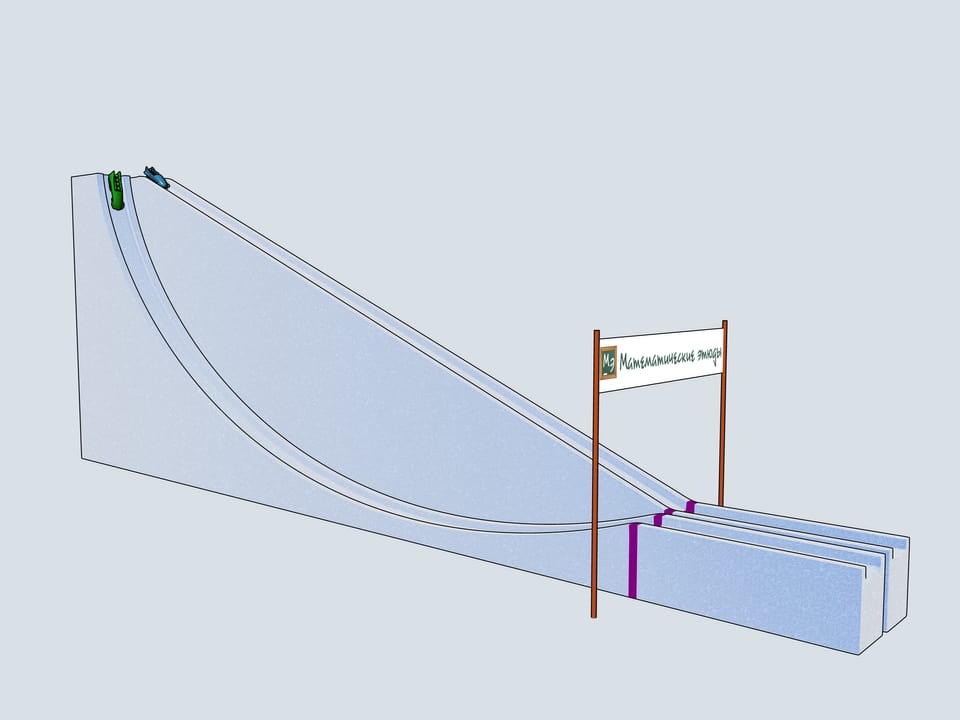
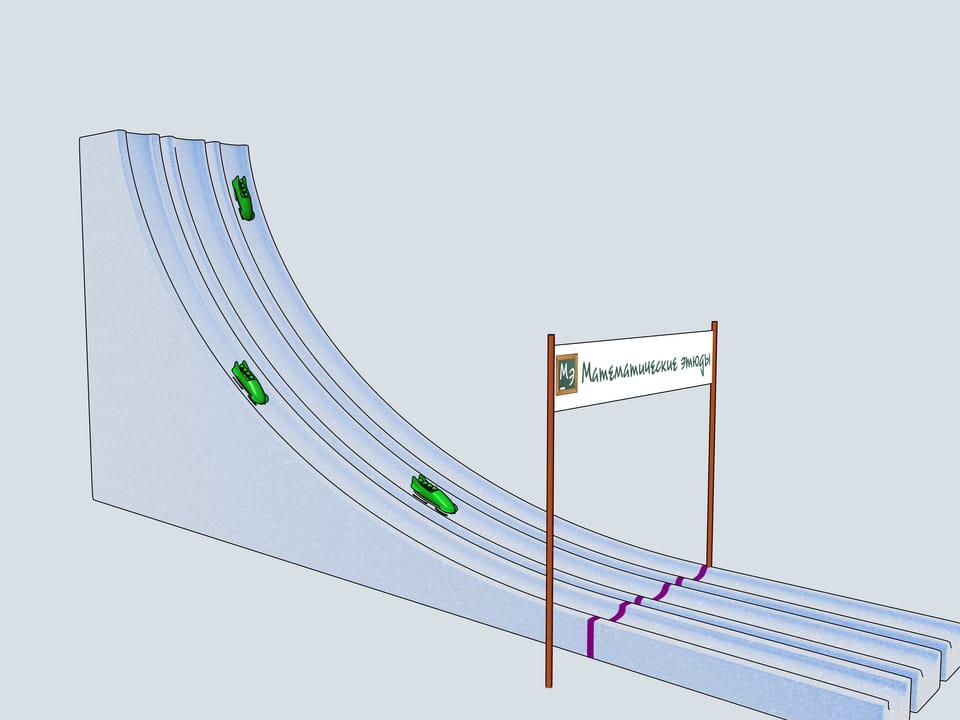
Сделаем бобслейные трассы с рассмотренными профилями и проследим, какой из бобов приедет первым.
История бобслея берёт своё начало в Швейцарии. В 1924 году во французском городе Шамони проходят первые зимние Олимпийские игры. На них уже проводятся соревнования по бобслею для экипажей двоек и четвёрок. Единственный год, когда на Олимпийских играх экипаж боба состоял из пяти человек, был 1928. С тех пор в бобслее всегда соревнуются мужские экипажи двойки и четвёрки. В правилах бобслея много интересного. Конечно же, существует ограничения на вес боба и команды, но существуют даже ограничения на материалы, которые можно использовать в коньках боба (передняя пара их подвижна и связана с рулём, задняя закреплена жёстко). Например, радий не может использоваться при изготовлении коньков.
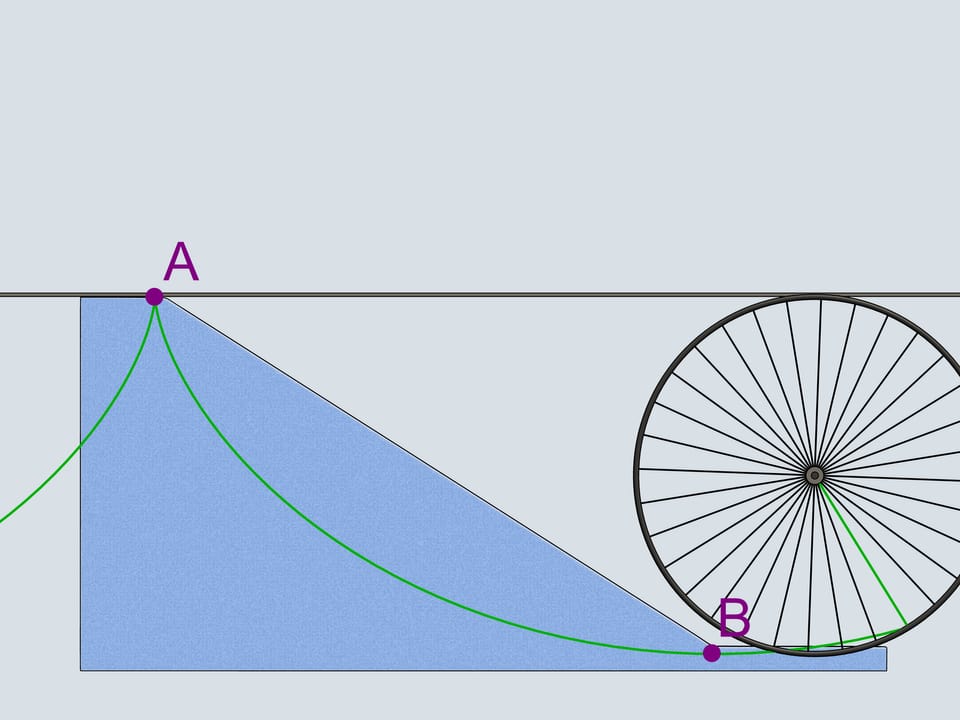
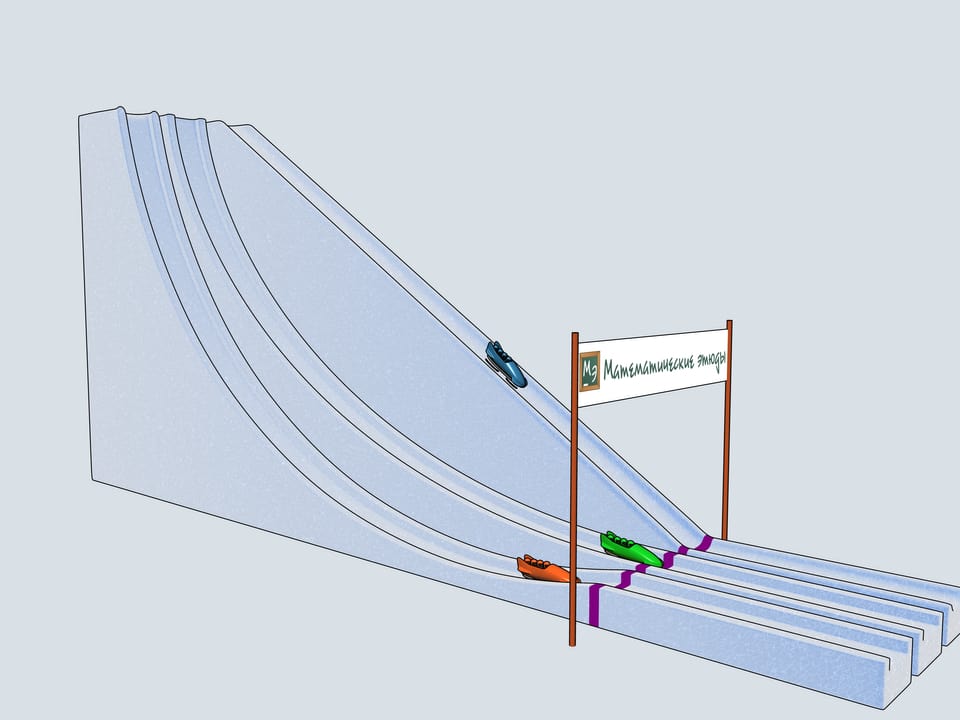
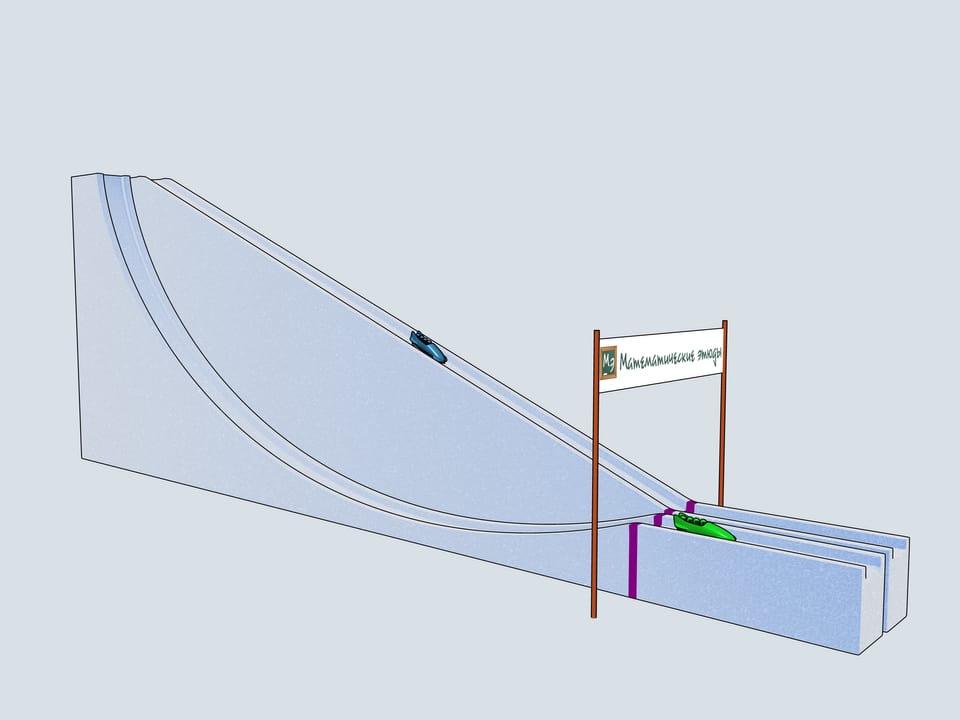
Дадим старт нашим четвёркам. Какой же боб первым приедет к финишу? Боб зелёного цвета, выступающий за команду Математических этюдов и катившийся по циклоидальной горке, приходит первым!
Почему же Галилео Галилей рассматривал четвертинку окружности и считал, что это наилучшая в смысле времени траектория спуска? Он вписывал в неё ломаные и заметил, что при увеличении числа звеньев время спуска уменьшается. Отсюда Галилей естественным образом перешёл к окружности, но сделал неверный вывод, что эта траектория наилучшая среди всех возможных. Как мы видели, наилучшей траекторией является циклоида.
Через две данные точки можно провести единственную циклоиду с условием, что в верхней точке находится точка возврата циклоиды. И даже когда циклоиде приходится подниматься, чтобы пройти через вторую точку, она всё равно будет кривой наискорейшего спуска!
Ещё одна красивая задача, связанная с циклоидой, — задача о таутохроне. В переводе с греческого ταύτίς означает «тот же самый», χρόνος, как мы уже знаем — «время».
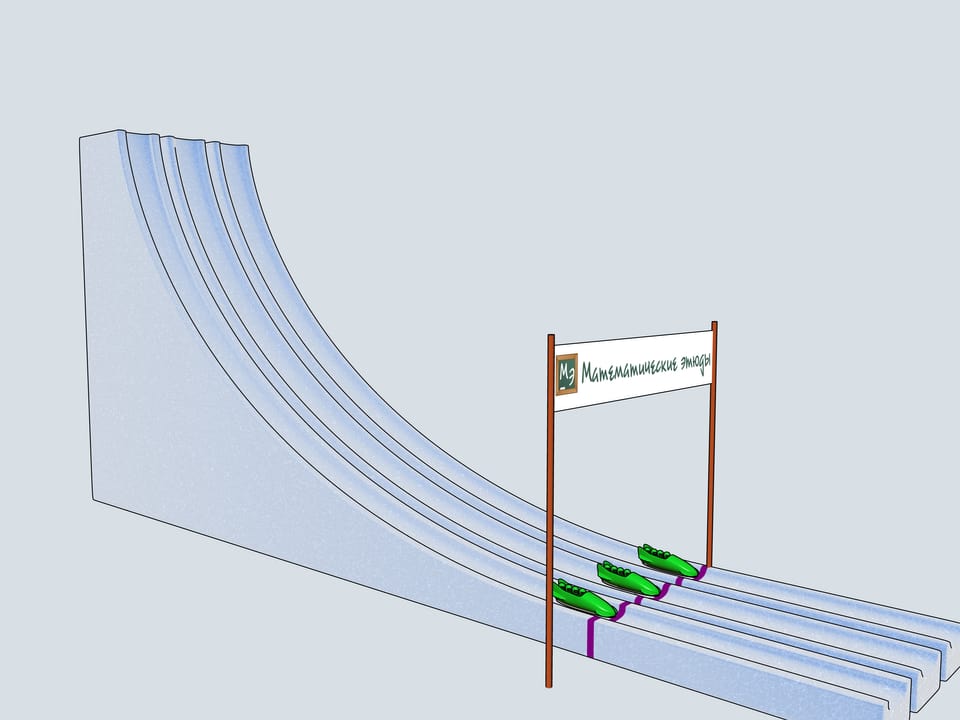
Сделаем три одинаковые горки с профилем в виде циклоиды, так, чтобы концы горок совпадали и располагались в вершине циклоиды. Поставим три боба на разные высоты и дадим отмашку. Удивительнейший факт — все бобы приедут вниз одновременно!
Зимой Вы можете построить во дворе горку изо льда и проверить это свойство вживую.
Задача о таутохроне состоит в нахождении такой кривой, что, начиная с любого начального положения, время спуска в заданную точку будет одинаковым.
Христиан Гюйгенс доказал, что единственной таутохроной является циклоида.
Конечно же, Гюйгенса не интересовал спуск по ледяным горкам. В то время учёные не имели такой роскоши заниматься науками из любви к искусству. Задачи, которые изучались, исходили из жизни и запросов техники того времени. В XVII веке совершаются уже дальние морские плавания. Широту моряки умели определять уже достаточно точно, но удивительно, что долготу не умели определять совсем. И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.
Первым, кто задумал делать маятниковые часы, которые были бы точны, был Галилео Галилей. Однако в тот момент, когда он начинает их реализовывать, он уже стар, он слеп, и за оставшийся год своей жизни учёный не успевает сделать часы. Он завещает это сыну, однако тот медлит и начинает заниматься маятником тоже лишь перед смертью и не успевает реализовать замысел. Следующей знаковой фигурой был Христиан Гюйгенс.
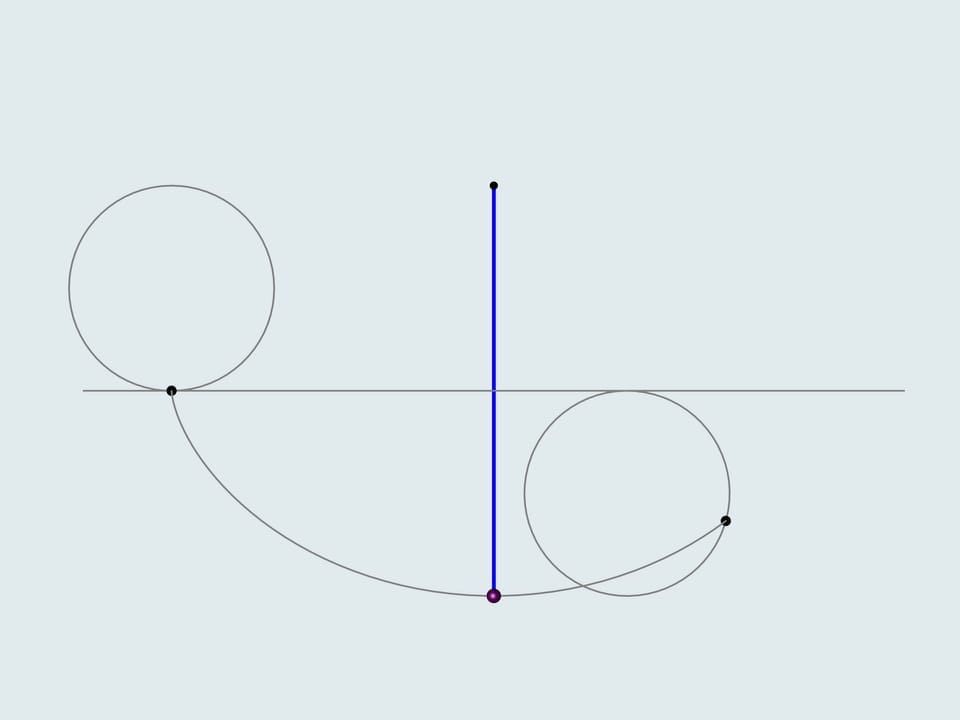
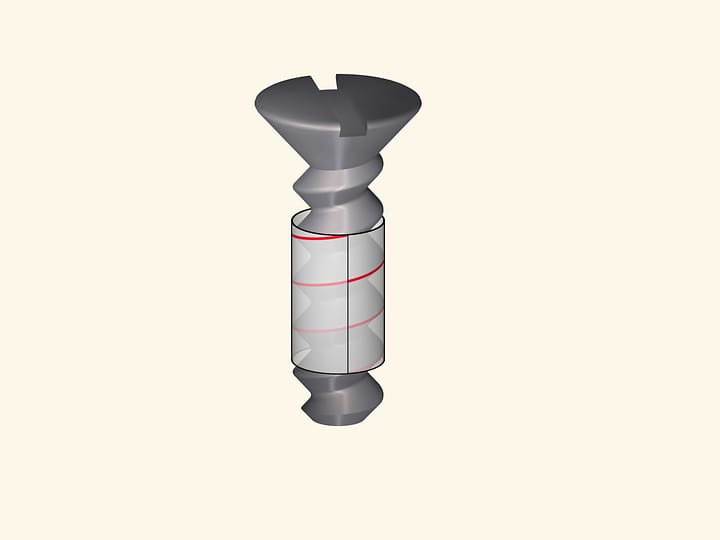
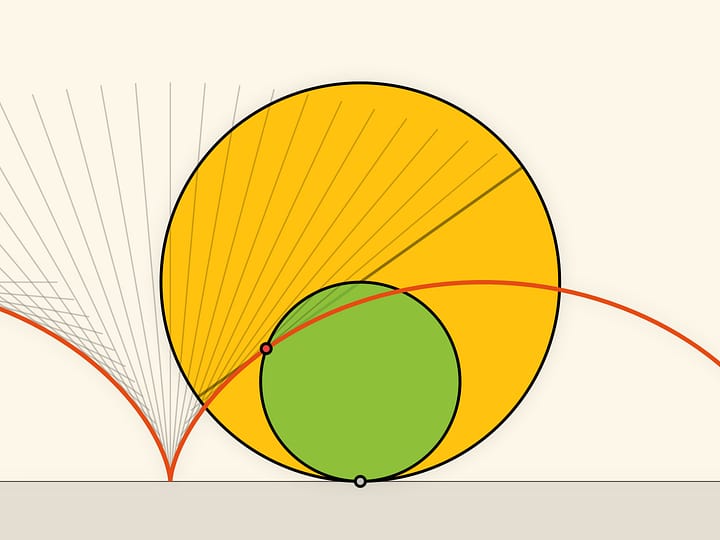
Он заметил, что период колебания обычного маятника, рассматривавшегося Галилеем, зависит от изначального положения, т. е. от амплитуды. Задумавшись о том, какова должна быть траектория движения груза, чтобы время качения по ней не зависело от амплитуды, он решает задачу о таутохроне. Но как заставить груз двигаться по циклоиде? Переводя теоретические исследования в практическую плоскость, Гюйгенс делает «щёчки», на которые наматывается веревка маятника, и решает ещё несколько математических задач. Он доказывает, что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой циклоиды является циклоида с теми же параметрами.
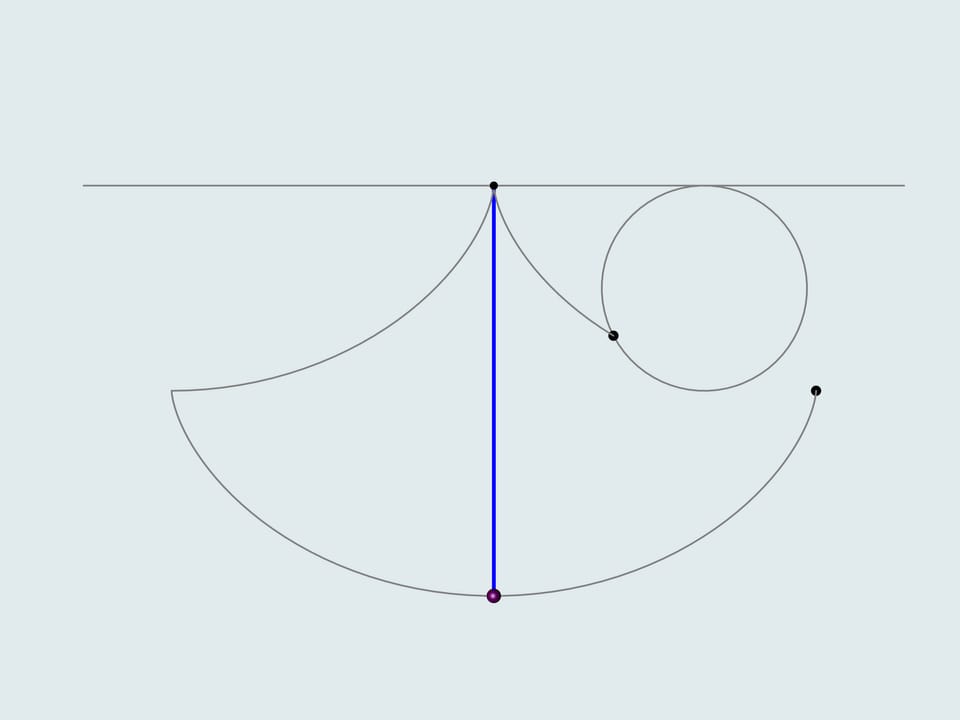
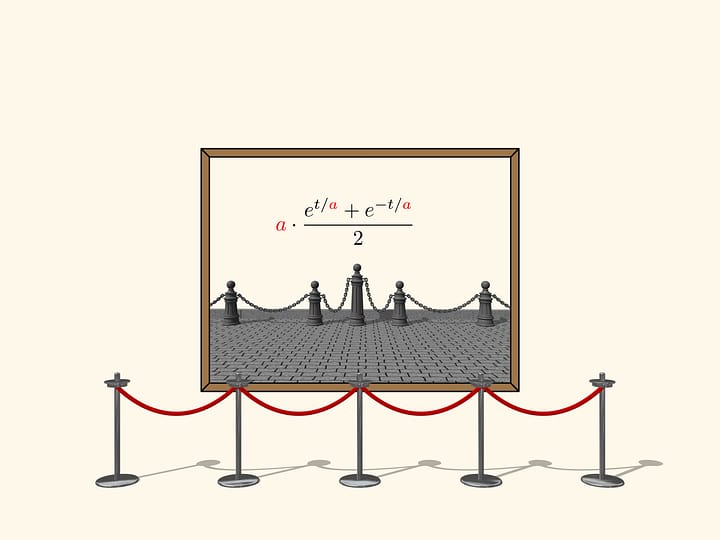
Кроме того, предложенная Гюйгенсом конструкция циклоидального маятника позволяет посчитать длину циклоиды. Если синюю ниточку, длина которой равна четырём радиусам производящего круга, максимально отклонить, то её конец будет в точке пересечения «щёчки» и циклоиды-траектории, т. е. в вершине циклоиды-«щёчки». Так как это половина длины арки циклоиды, то полная длина равна восьми радиусам производящего круга.
Христиан Гюйгенс сделал циклоидальный маятник, и часы с ним проходили испытания в морских путешествиях, но не прижились. Впрочем, так же, как и часы с обычным маятником для этих целей.
Отчего же, однако, до сих пор существуют часовые механизмы с обыкновенным маятником? Если приглядеться, то при малых отклонениях, как у красного маятника, «щёчки» циклоидального маятника почти не оказывают влияния. Соответственно, движение по циклоиде и по окружности при малых отклонениях почти совпадают.
Литература
Берман Г. Н. Циклоида. — М. : Наука, 1980.
Гиндикин С. Г. Рассказы о физиках и математиках. — М. : МЦНМО, 2006.