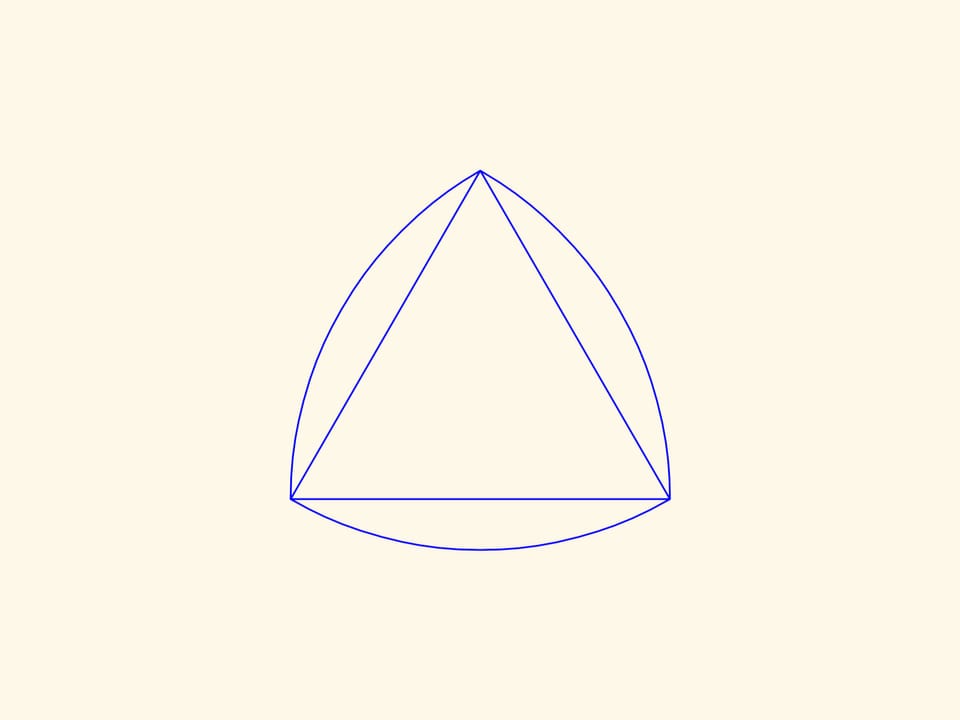
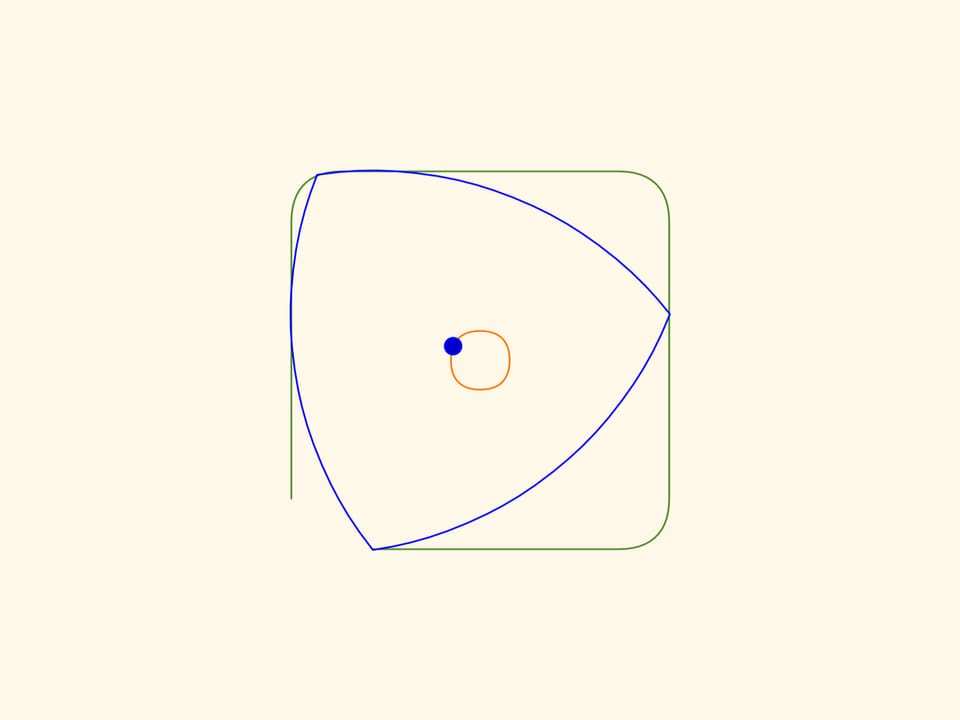
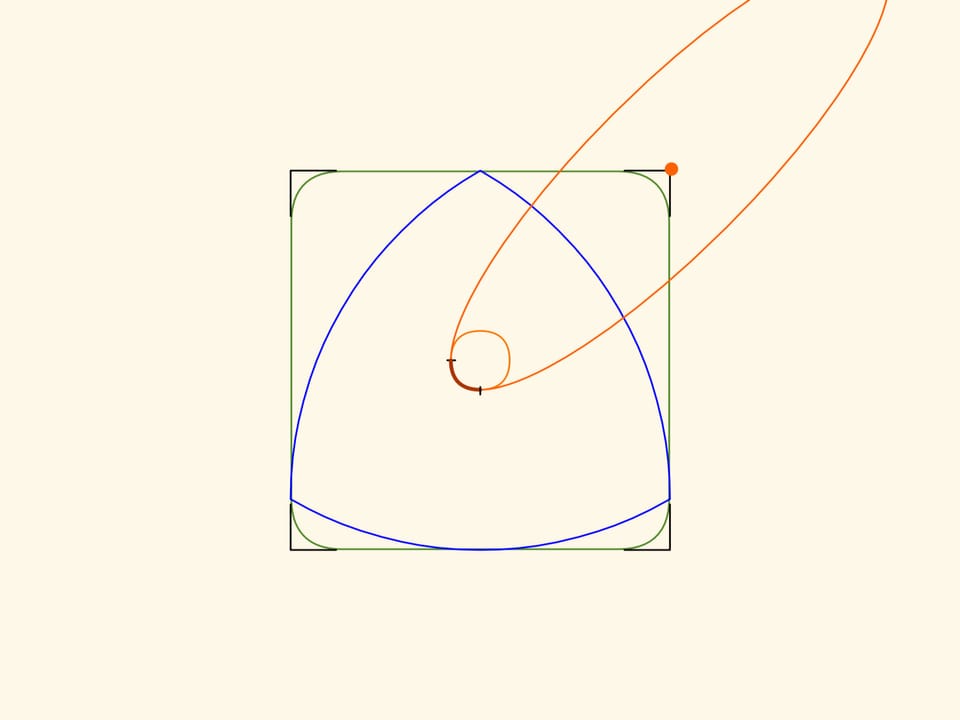
В фильме «Круглый треугольник Рело» рассказывается о фигурах, обладающих постоянной шириной. Именно треугольник Рело — простейшая фигура постоянной ширины — поможет нам в сверлении квадратных отверстий. Если двигать центр этого «треугольника» по некой траектории, то его вершины вычертят почти квадрат, а сам он заметёт всю площадь внутри полученной фигуры.
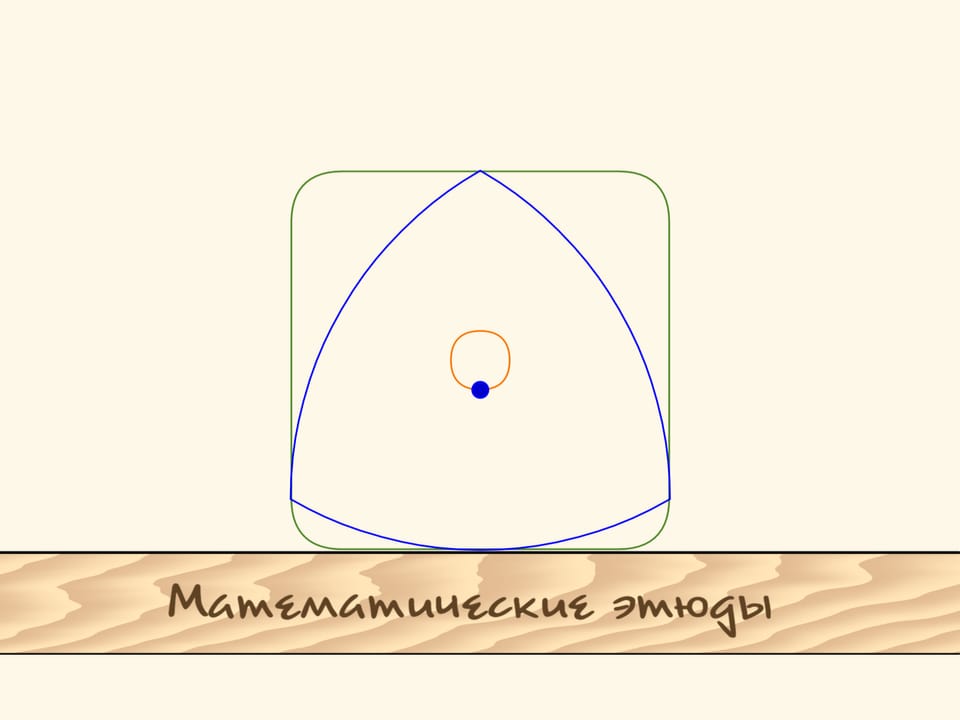
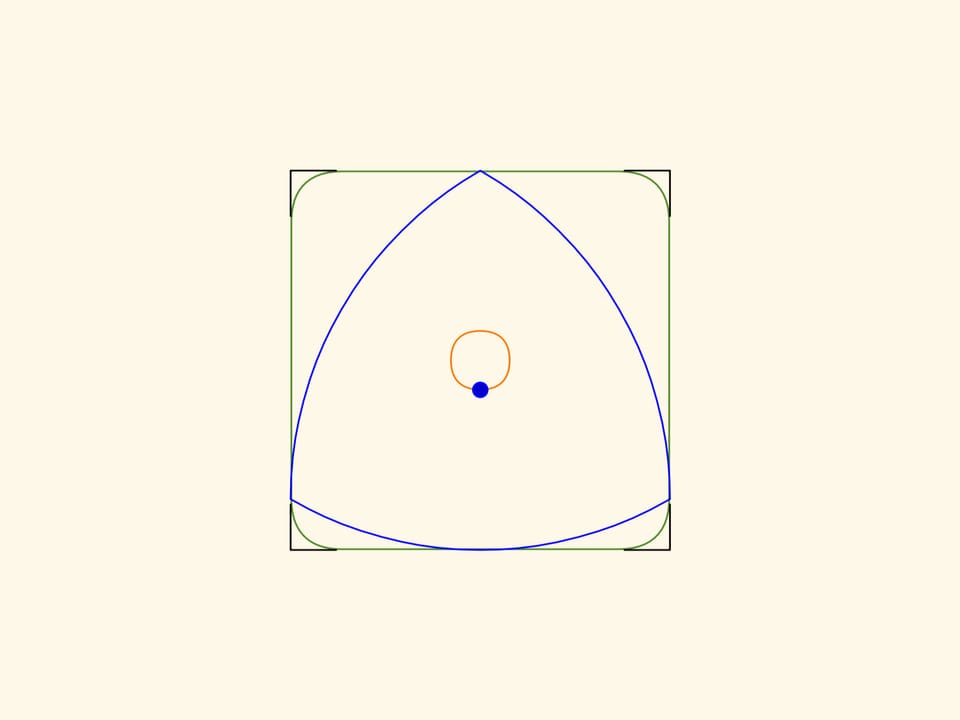
Границы полученной фигуры, за исключением небольших кусочков по углам, будут строго прямыми! И если продолжить отрезки, тем самым добавив уголочки, то получится в точности квадрат.
Для того, чтобы получилось описанное выше, центр треугольника Рело нужно двигать по траектории, являющейся склейкой из четырех одинаковых дуг эллипсов. Центры эллипсов расположены в вершинах квадрата, а полуоси, повёрнутые на угол $45^\circ$ относительно сторон квадрата, равны $k\cdot(1+1/\sqrt{3})/2$ и $k\cdot(1-1/\sqrt{3})/2$, где $k$ — длина стороны вычерчиваемого квадрата.
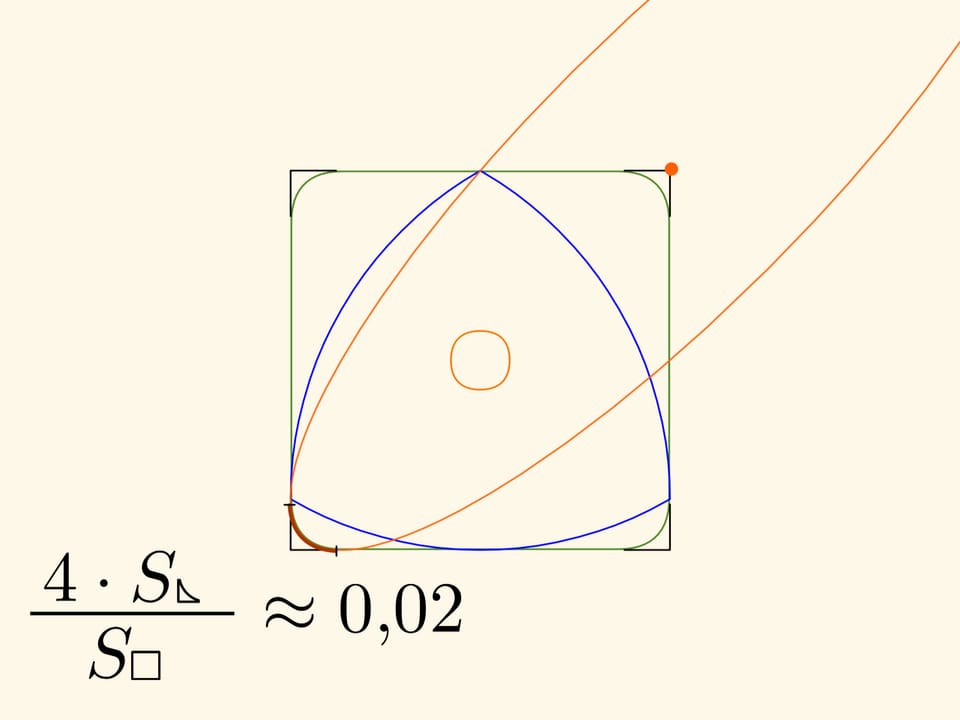
Кривые, скругляющие углы, также являются дугами эллипсов с центрами в углах квадрата, их полуоси повёрнуты на угол $45^\circ$ относительно сторон квадрата и равны $k\cdot(\sqrt{3}+1)/2$ и $k\cdot(1/\sqrt{3}-1)/2.$
Площадь незаметённых уголочков составляет всего около $2\%$ от площади всего квадрата!
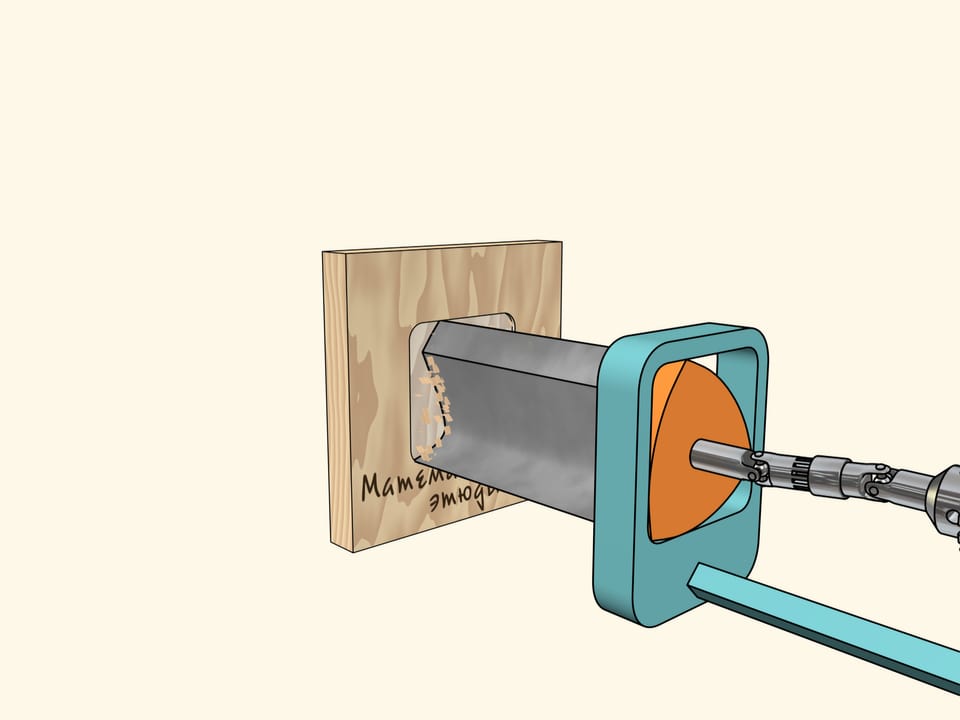
Теперь, если сделать сверло в виде треугольника Рело, то можно будет сверлить квадратные отверстия с немного скругленными уголками, но абсолютно прямыми сторонами!
Осталось сделать такое сверло… Вернее, само-то сверло сделать несложно, нужно только чтобы оно напоминало в сечении треугольник Рело, а режущие кромки совпадали с его вершинами.
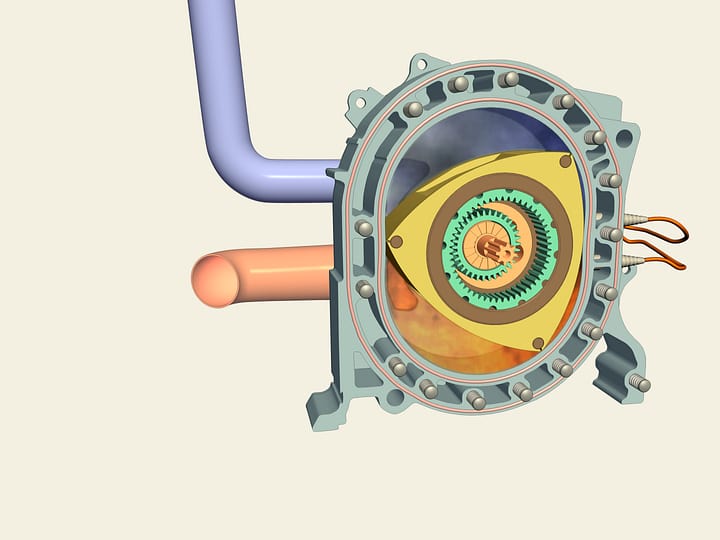
Трудность заключается в том, что, как уже было отмечено выше, траектория центра сверла должна состоять из четырёх дуг эллипсов. Визуально эта кривая очень похожа на окружность и даже математически близка к ней, но всё же это не есть окружность. А все эксцентрики (круг, посаженный на круг другого радиуса со смещённым центром), используемые в технике, дают движение строго по окружности.
В 1914 году английский инженер Гарри Джеймс Уаттс придумывает, как устроить такое сверление. На поверхность он накладывает направляющий шаблон с прорезью в виде квадрата, в котором ходит сверло, вставленное в патрон со «свободно плавающим в нём сверлом». Патент на такой патрон был выдан фирме, начавший изготовление свёрл Уаттса в 1916 году.
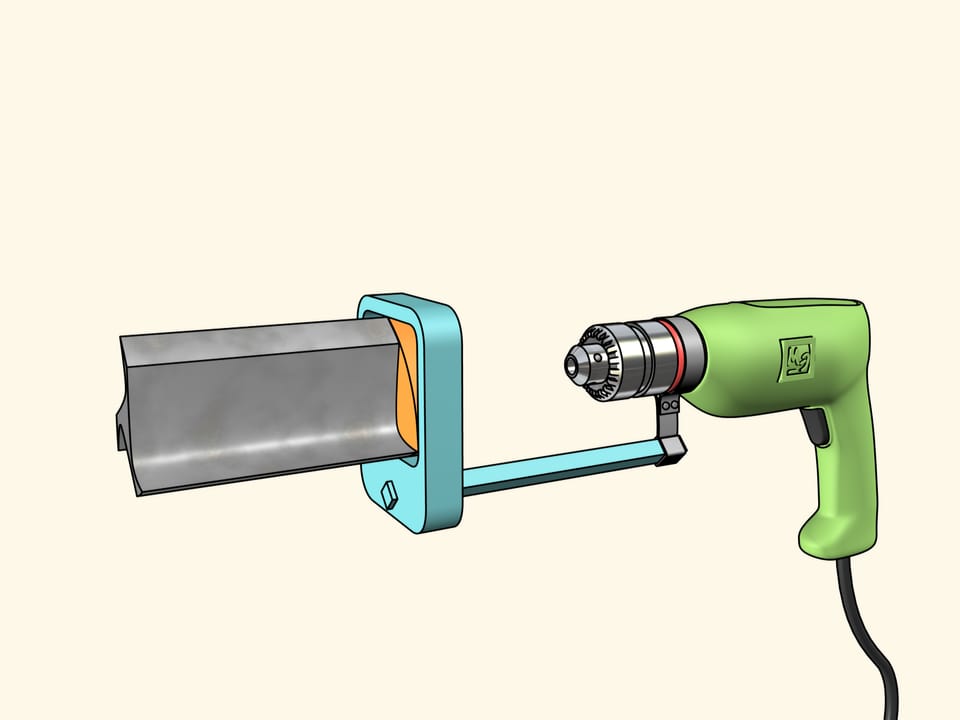
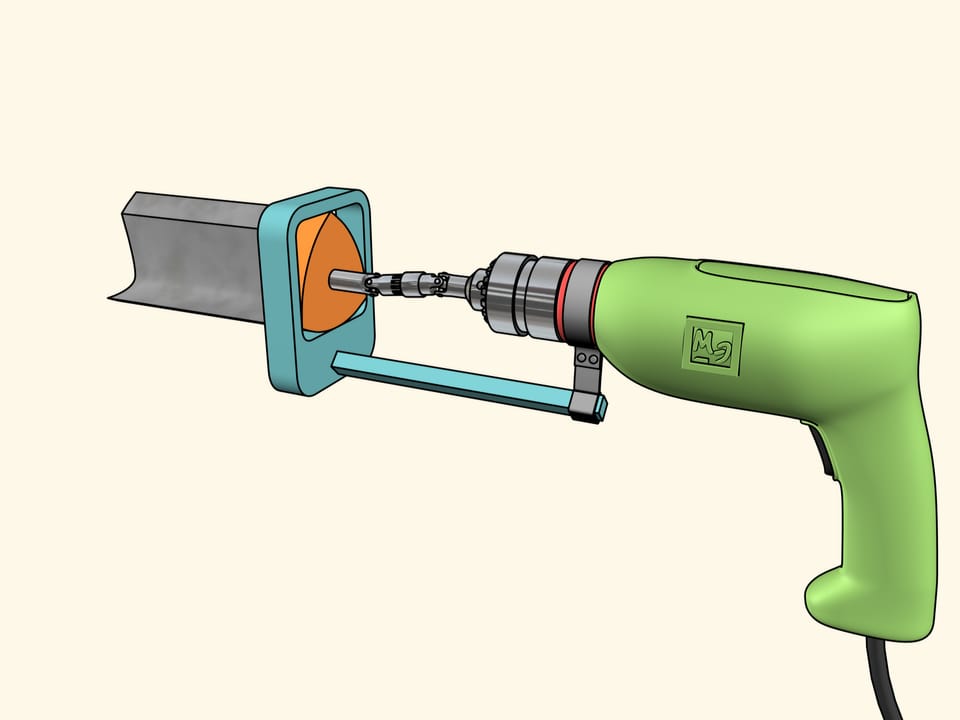
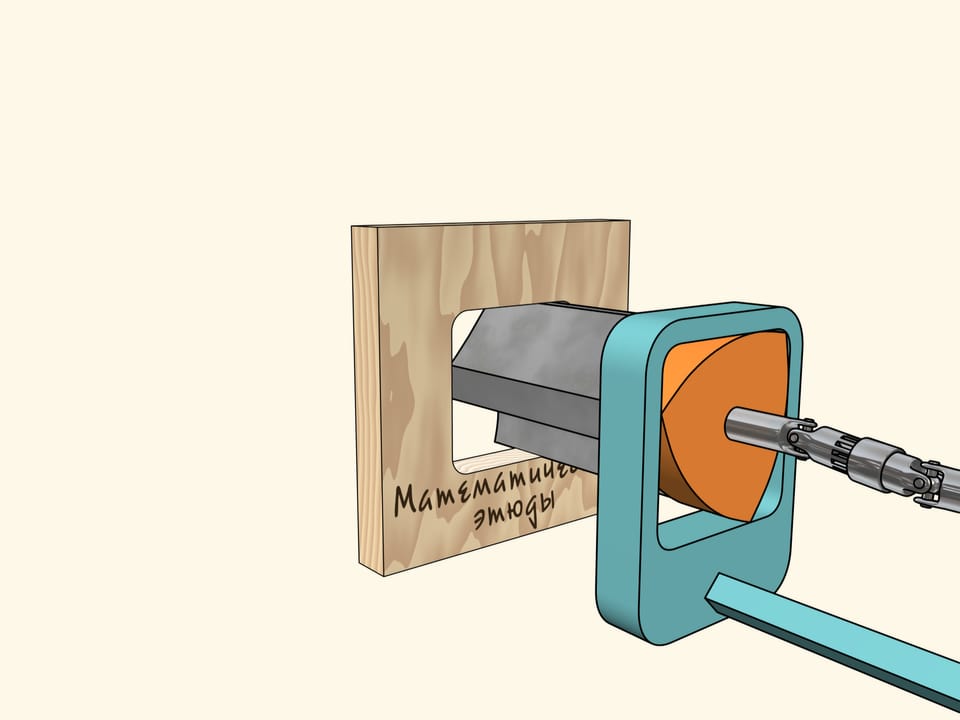
Мы же воспользуемся другой известной конструкцией. Прикрепим сверло жёстко к треугольнику Рело, помещённому в квадратную направляющую рамку. Сама рамка фиксируется на дрели. Осталось теперь передать вращение патрона дрели треугольнику Рело.
Помогает решить эту техническую проблему конструкция, которую вы наверняка много раз видели под днищем проезжавших по улице грузовых автомобилей — карданный вал. Эта передача получила своё название в честь Джероламо Кардано.
Джероламо КАРДАНО 1501—1576
Когда в 1541 году император Карл V триумфально вошёл в завоёванный Милан, ректор коллегии врачей Кардано шёл рядом с балдахином.
В ответ на оказанную честь он предложил снабдить королевский экипаж подвеской из двух валов, качение которых не выведет
карету из горизонтального положения […]. Справедливость требует отметить, что идея такой системы восходит к античности и что по крайней
мере в «Атлантическом кодексе» Леонардо да Винчи имеется рисунок судового компаса с карданным подвесом. Такие компасы получили
распространение в первой половине XVI века, по-видимому, без влияния Кардано.
Гиндикин С. Г. Рассказы о физиках и математиках.
Теперь у нас всё готово к сверлению. Возьмём фанерный лист и… высверлим квадратное отверстие! Как уже говорилось, стороны будут строго прямыми и лишь уголки немного скруглены. При необходимости их можно подправить надфилем.
Литература
Weisstein E. Reuleaux Triangle.
Гиндикин С. Г. Рассказы о физиках и математиках. — М. : МЦНМО, 2006.
Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 84—85, 319—320.