Число степеней свободы — это количество независимых параметров, однозначно определяющих положение механической системы.
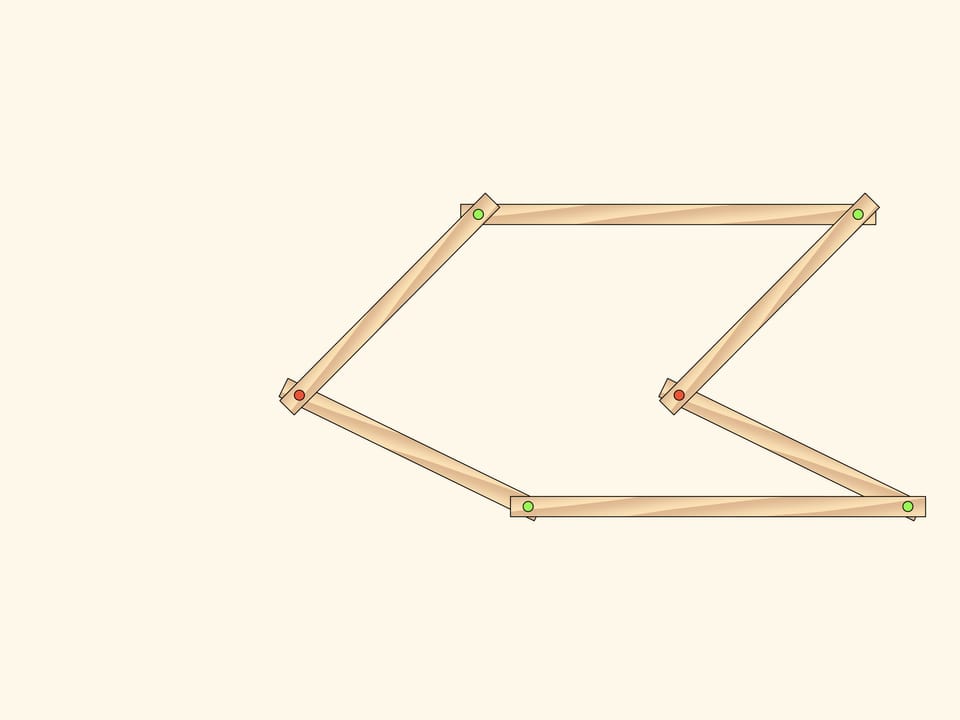
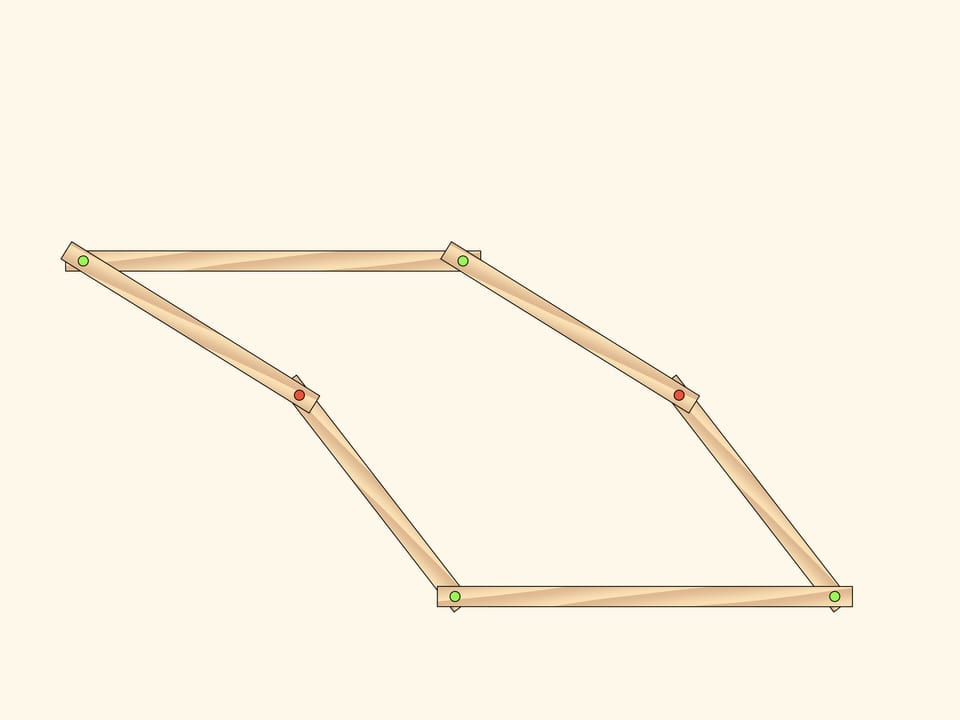
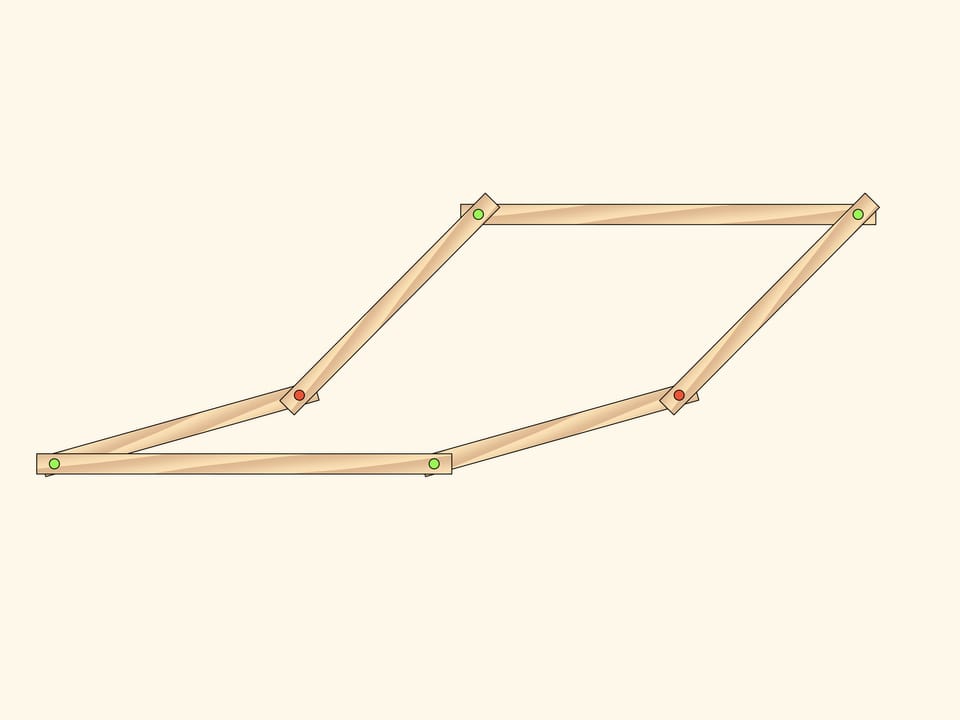
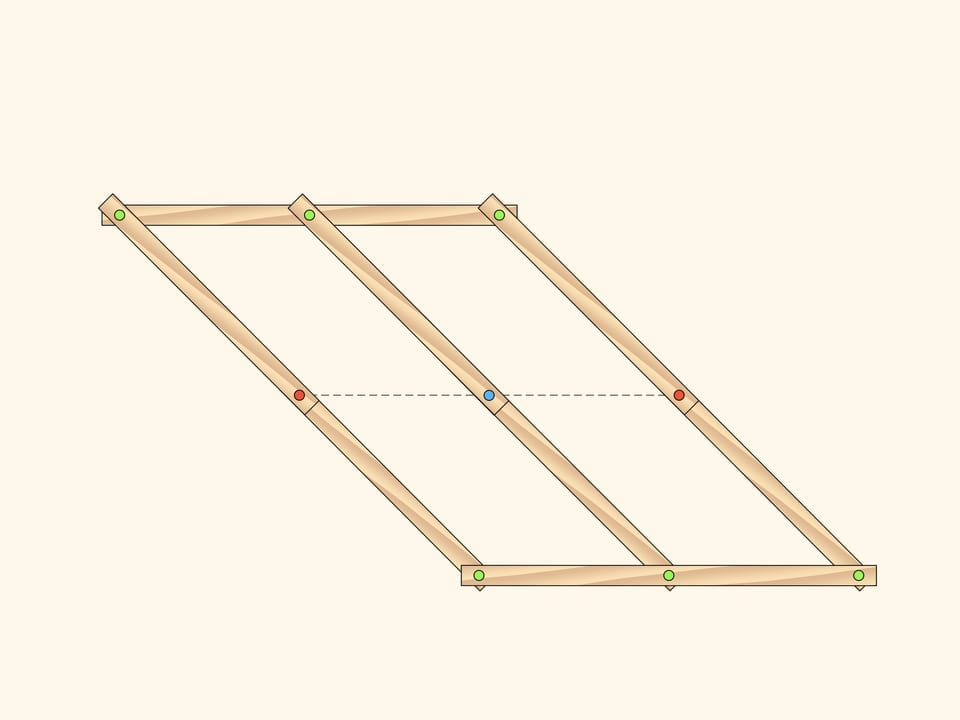
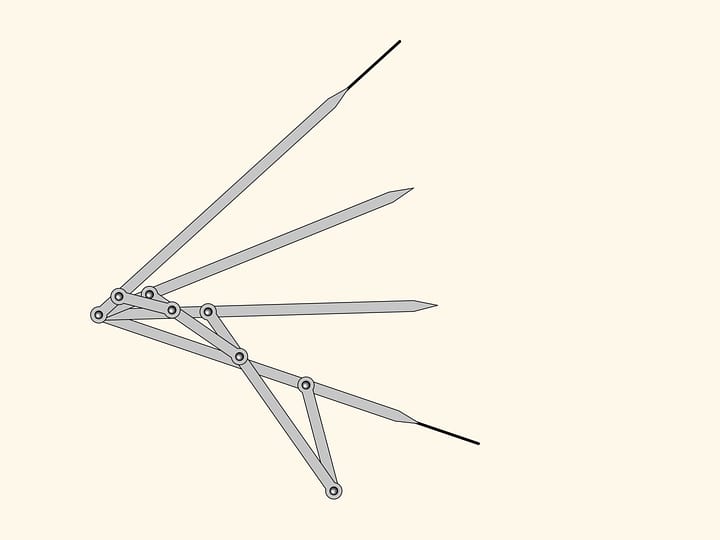
Рассмотрим плоский шарнирный механизм, состоящий из двух одинаковых параллелограммов, имеющих два общих закреплённых красных шарнира. Число степеней свободы такого механизма, конечно, равно двум, так как параллелограммы могут вращаться независимо друг от друга, и в качестве параметров можно, например, выбрать углы поворота параллелограммов, отсчитываемые от горизонтали.
Всегда ли за конкретным механизмом «закреплено» определённое неизменное число степеней свободы? Или же бывают механизмы, у которых число степеней свободы переменно? Оказывается, бывают…
Первый плоский шарнирный механизм с переменным числом степеней свободы был придуман В. Вундерлихом в 1954 году. Он состоял из двух закреплённых шарниров и 12 звеньев. Мы же рассмотрим более простой механизм с девятью звеньями, придуманный российским математиком Михаилом Ковалёвым.
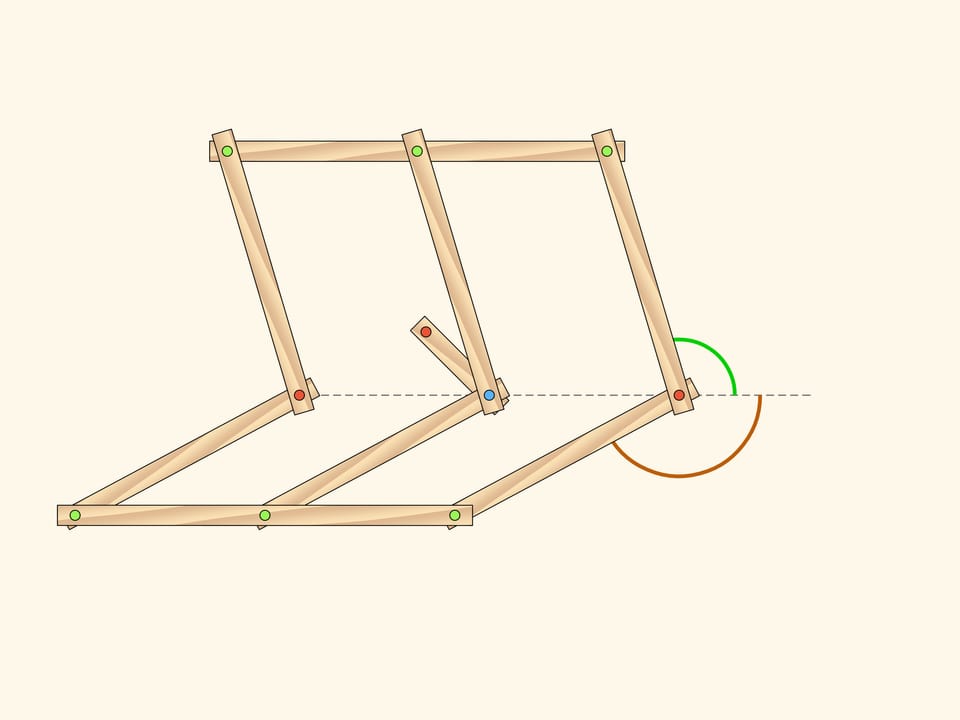
Добавим к параллелограммам «средние линии» и из точки их пересечения проведём ещё одно короткое звено, оканчивающееся на другом конце закреплённым красным шарниром.
Пока синий шарнир остается на центральной линии, соединяющей два изначальных неподвижных красных шарнира, добавленные звенья не влияют на количество степеней свободы механизма. Его положение задаётся, например, двумя углами поворота параллелограммов, отсчитываемых от горизонтали.
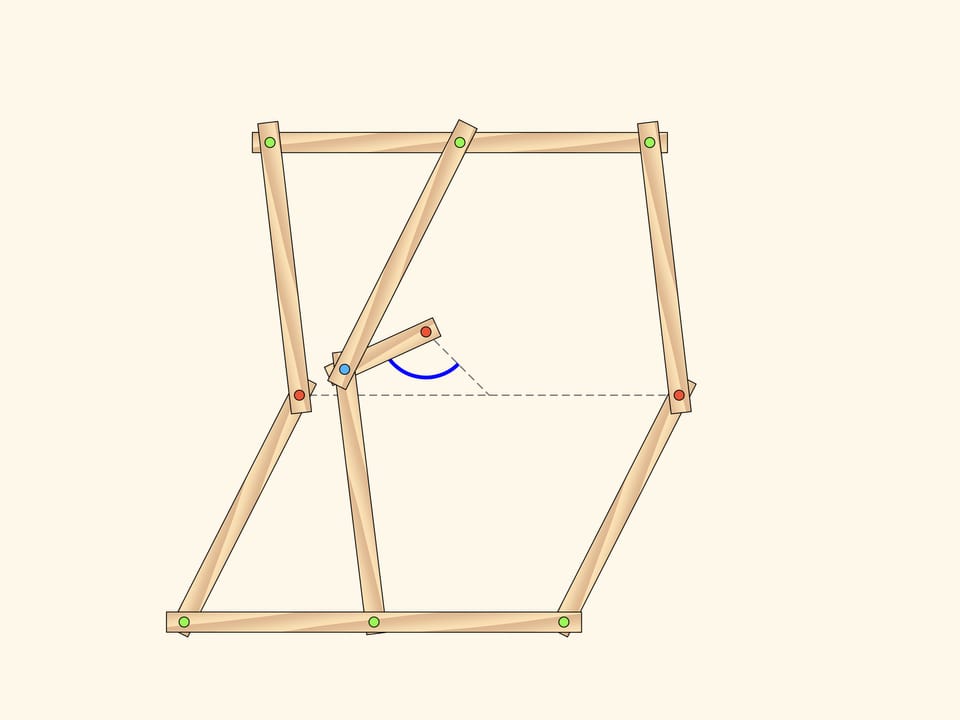
Однако синий шарнир может уйти с центральной линии в момент, когда средние линии и маленькое звено лежат на одной прямой. И как только синий шарнир уходит с центральной линии, положение всего механизма начинает определяться лишь одним параметром! В качестве этого параметра можно выбрать, например, угол между изначальным положением добавленного короткого звена и его положением в данный момент времени.
Литература
Wunderlich W. Ein merkwürdiges Zwölfstabgetriebe // Österreichisches Ingenieurarchiv, 1954. — Band 8, Heft 2/3. — S. 224—228.
Wohlhart K. Kinematotropic Linkages // Recent Advances in Robot Kinematics. — Kluwer Academic Publishers, 1996.
Ковалёв М. Д. Геометрическая теория шарнирных устройств // Известия РАН. Серия математическая. — 1994. — Т. 58, № 1. — C. 45—70.