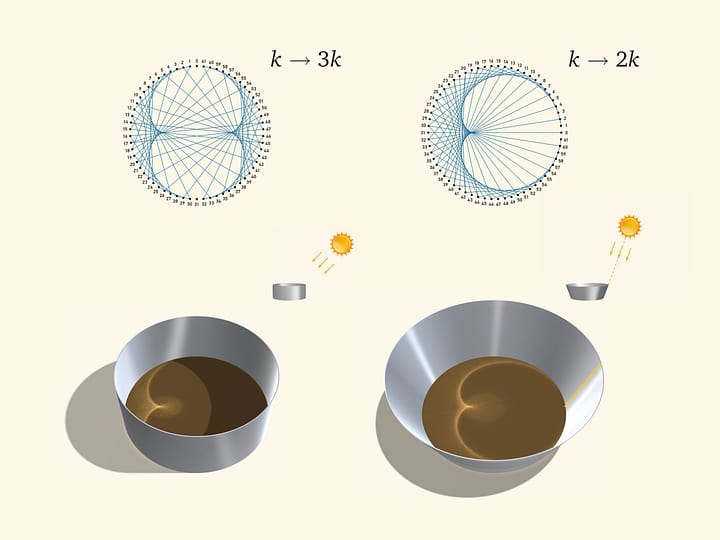
Знакомая с детства картинка. Калейдоскоп. Название происходит от древнегреческих слов καλός — красивый, εἶδος — вид, σκοπέω — смотрю, наблюдаю. Этот оптический прибор-игрушка был изобретён учёным-физиком в начале XIX века и быстро стал любимой забавой во многих странах, включая Россию.
Те, кто в исследовательских целях разбирал в детстве калейдоскоп, помнят, что внутри цилиндрической тубы расположены три зеркала в виде длинных прямоугольников. Они образуют зеркальную треугольную призму. За треугольником в основании призмы, который будем называть фундаментальным, расположен объём, в котором при вращении калейдоскопа пересыпаются мелкие разноцветные предметы, составляя случайную картинку. Образовавшаяся в фундаментальном треугольнике картинка отражается в зеркалах и красивым образом заполняет всю плоскость изображения.
Для каждого человека слова «красивым образом» значат что-то своё, тем не менее, попробуем выделить какие-то математические свойства в образующемся в калейдоскопе изображении.
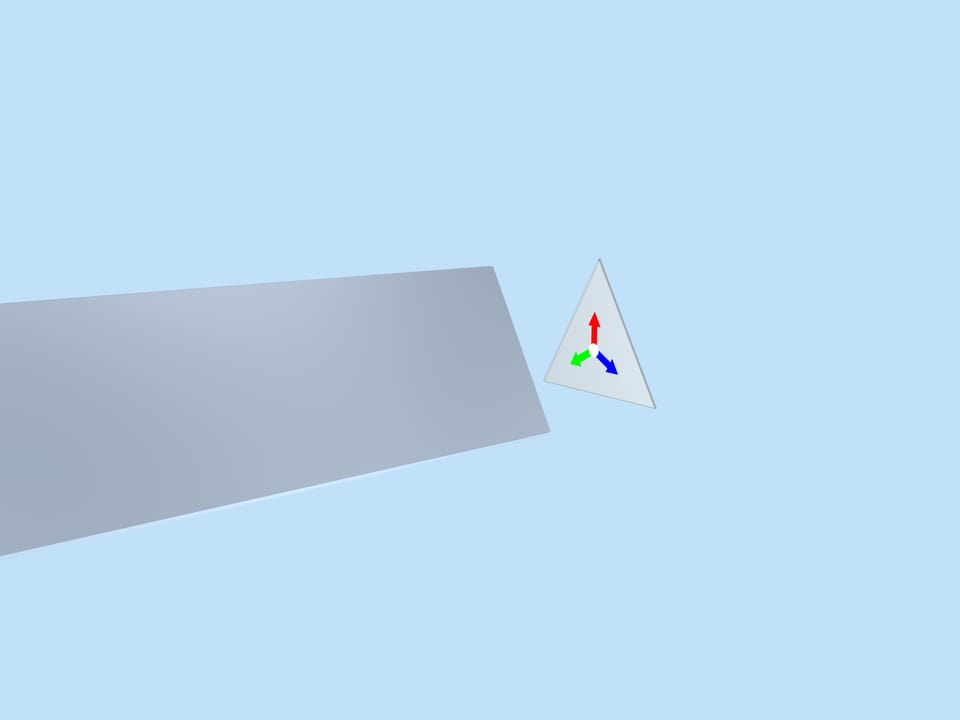
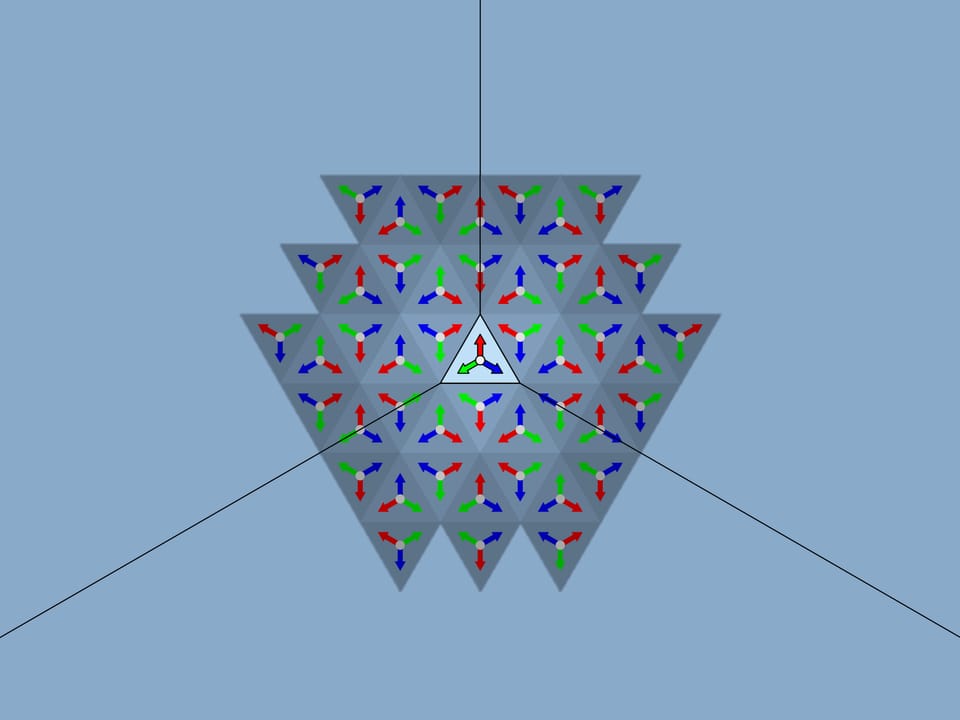
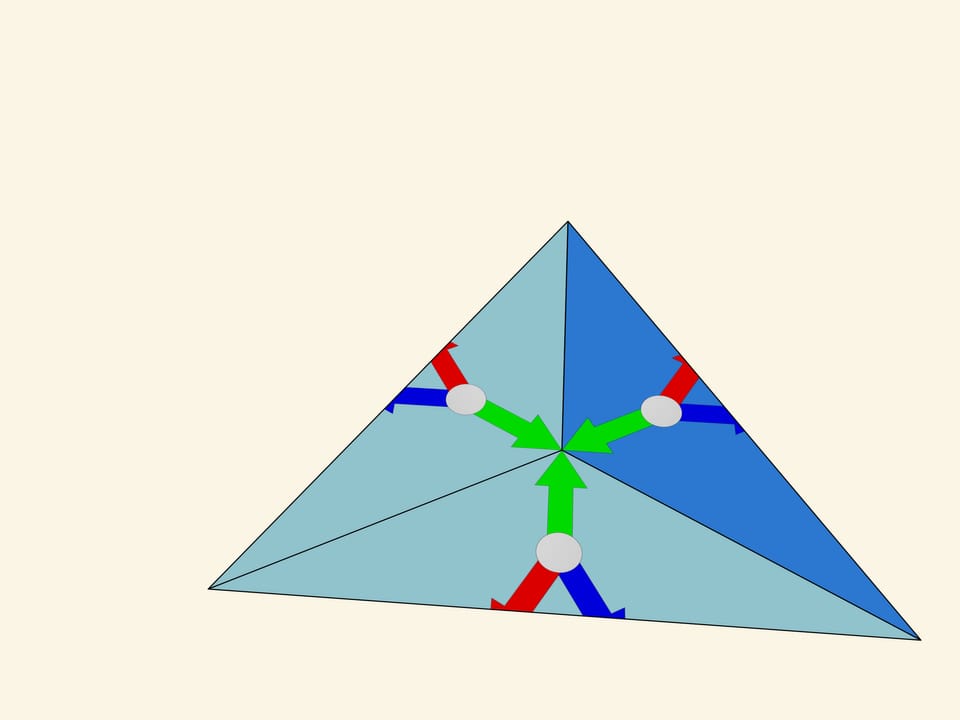
Картинка, образующаяся в фундаментальном треугольнике в конкретный момент, конечно же, влияет на красоту общего изображения, но она случайная и меняется при вращении, а значит, от неё наши рассуждения зависеть не должны. Заменим её на более простую, математически связанную с самим фундаментальным треугольником — три разноцветные стрелки одинаковой длины, отложенные от центра треугольника перпендикулярно зеркалам.
«Красота» изображения в калейдоскопе зависит от того, какой фундаментальный треугольник отражается в зеркалах. Получающаяся картина должна заполнять всю плоскость, различные копии-отражения фундаментального треугольника не должны накладываться друг на друга, создавая мешанину, не должны обрезаться. Ну а главная характеристика «правильного» калейдоскопа — изображение, получившееся после отражёния в зеркалах, наблюдатель должен видеть как реальный объект: если смещаться относительно зеркал, то изображение не должно изменяться.
Какими могут быть углы фундаментального треугольника (углы между зеркалами), чтобы выполнялись сформулированные свойства?
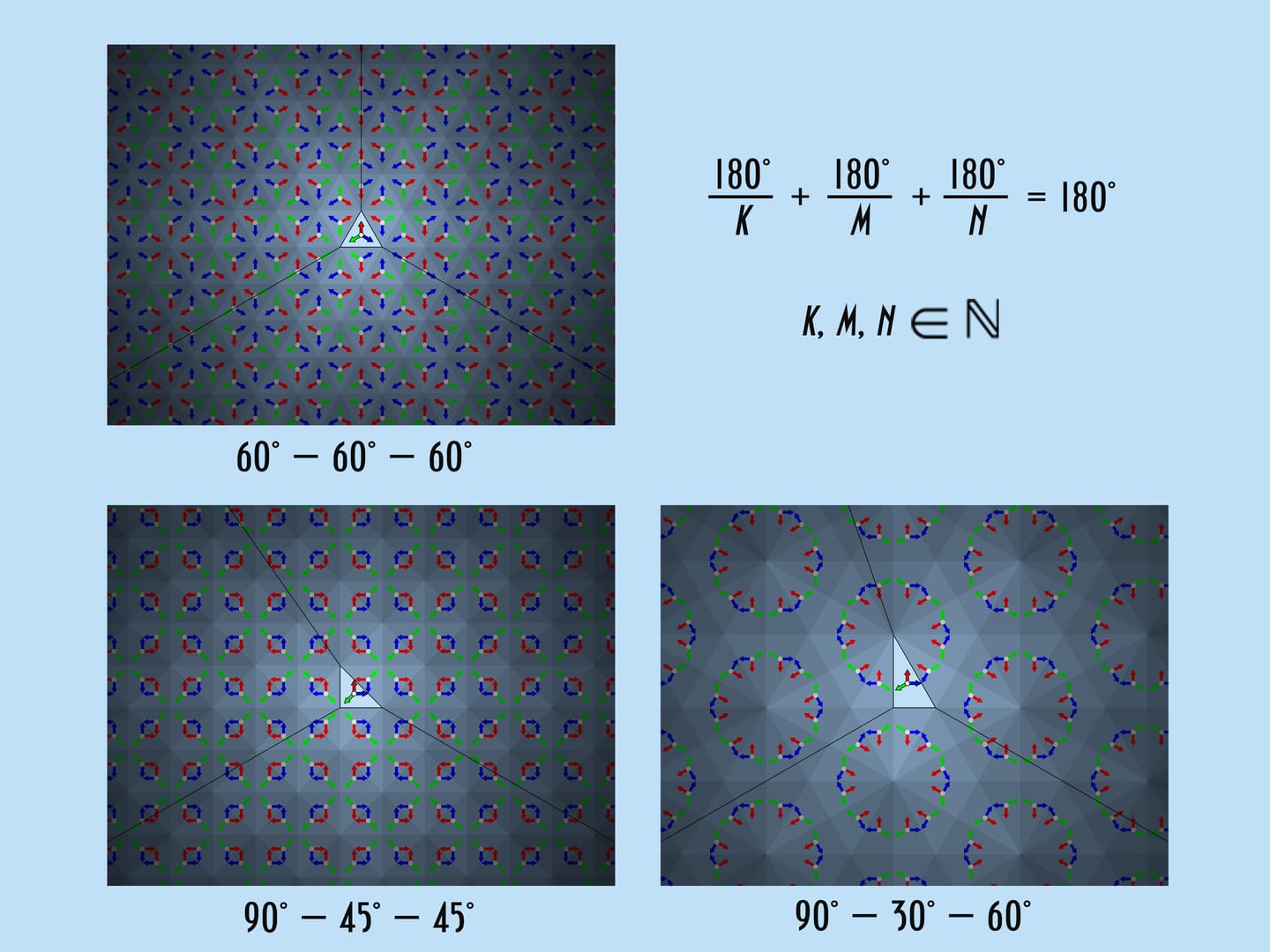
В самом распространённом типе калейдоскопов треугольник в основании призмы — равносторонний, с углами $60^\circ$—$60^\circ$—$60^\circ$. Это удобно и с производственной точки зрения — все зеркала одинаковые. Возможны ли какие-то другие наборы углов?
Попробуем сделать зеркальную призму с основанием в виде произвольного треугольника. После отражений наблюдатель будет видеть множество обломков картинки, образовавшейся в фундаментальном треугольнике и в целом изображение красивым не будет. Так что красивая картинка — большая удача.
Кроме равностороннего треугольника с углами $60^\circ$—$60^\circ$—$60^\circ$ существуют ещё только два треугольника, дающих красивую картинку. Это прямоугольные треугольники с углами $90^\circ$—$45^\circ$—$45^\circ$ и $90^\circ$—$30^\circ$—$60^\circ$. Чтобы убедиться в этом, математически построим изображение, возникающее в калейдоскопе.
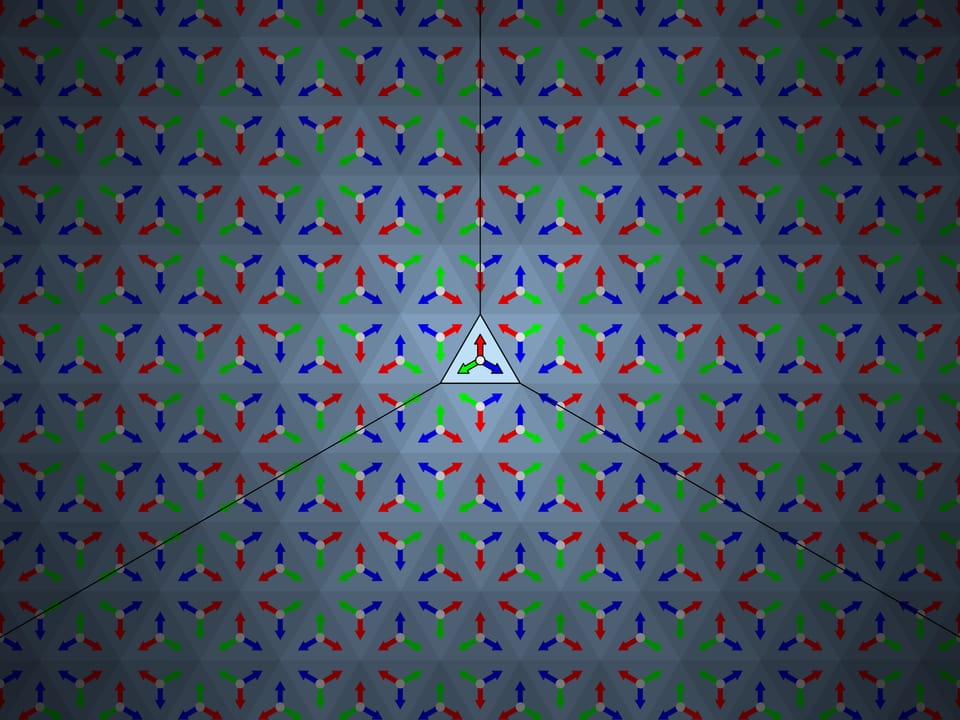
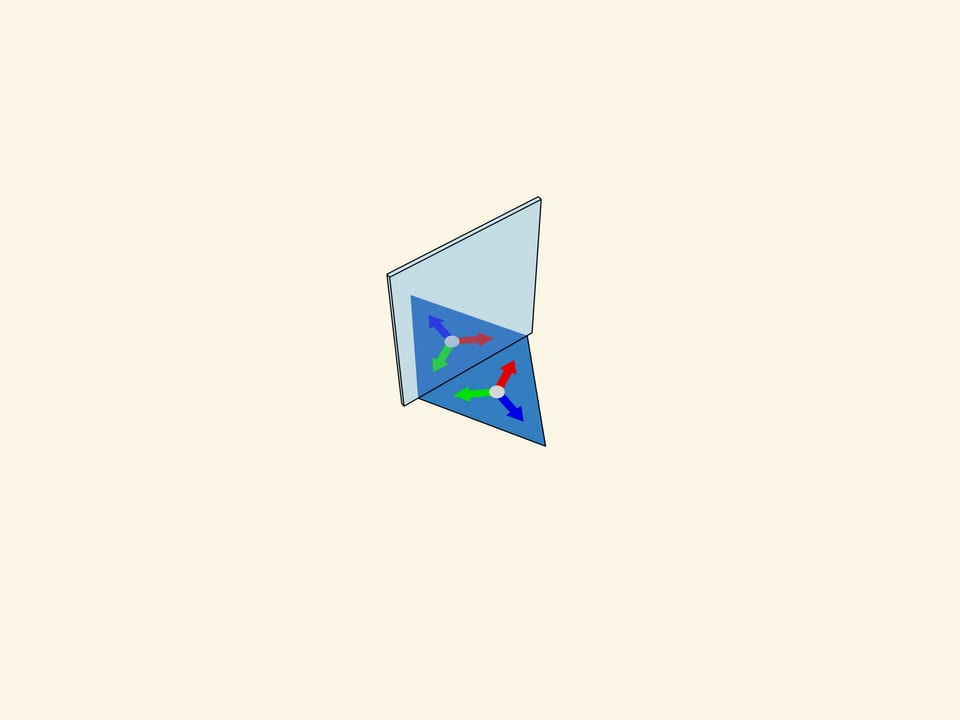
Возьмём стандартный фундаментальный треугольник с углами $60^\circ$—$60^\circ$—$60^\circ$. Что с точки зрения математики значит физическое отражение треугольника в зеркале, содержащем его сторону и перпендикулярном его плоскости? Это добавление к изначальному треугольнику симметричного ему относительно стороны, вдоль которой расположено зеркало. Если бы у нас было одно зеркало, то на этом всё бы и закончилось; общая картинка состояла бы из фундаментального треугольника и его образа в зеркале. Но в случае калейдоскопа все три стороны фундаментального треугольника зеркальные, и, значит, наблюдатель заведомо увидит сам фундаментальный треугольник и три его симметричные относительно сторон копии. На самом же деле, как известно из практики, картинка будет гораздо больше.
Дело в том, что отражения зеркала в зеркале снова «работают» как зеркало. То есть природа продолжает симметрично отражать копии треугольников относительно их «виртуальных» сторон.
Вот уже возникает первое условие на фундаментальный треугольник: при последовательных симметриях относительно всех его сторон, а затем сторон его копий, образы должны замощать (покрывать без наложений) всю плоскость. При этом порядок, в котором производятся отражения при последовательном построении изображения, не должен влиять на окончательный результат, — наш глаз видит сразу все лучи, формирующие и отражения первого порядка, и отражения второго порядка и т.д.
Изображение, наблюдаемое в традиционном равноугольном калейдоскопе, действительно совпадает с полученным рассмотренным математическим способом. И оно действительно устойчиво: если покачать калейдоскоп, то изображение меняться не будет. Даже в тех местах, где ребро между зеркалами калейдоскопа перемещается относительно рисунка, он остается постоянным вне зависимости от положения калейдоскопа и его рёбер.
У калейдоскопов, построенных на фундаментальных треугольниках с наборами углов $90^\circ$—$45^\circ$—$45^\circ$ и $90^\circ$—$30^\circ$—$60^\circ$, все описанные свойства также выполняются. А бывают ли еще какие-то случаи?
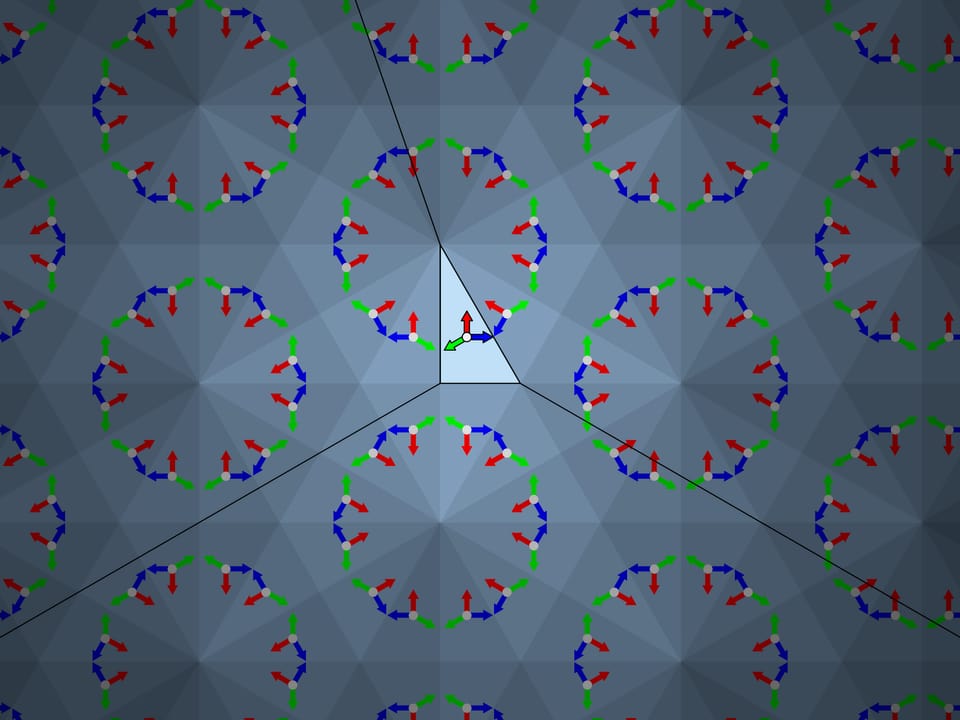
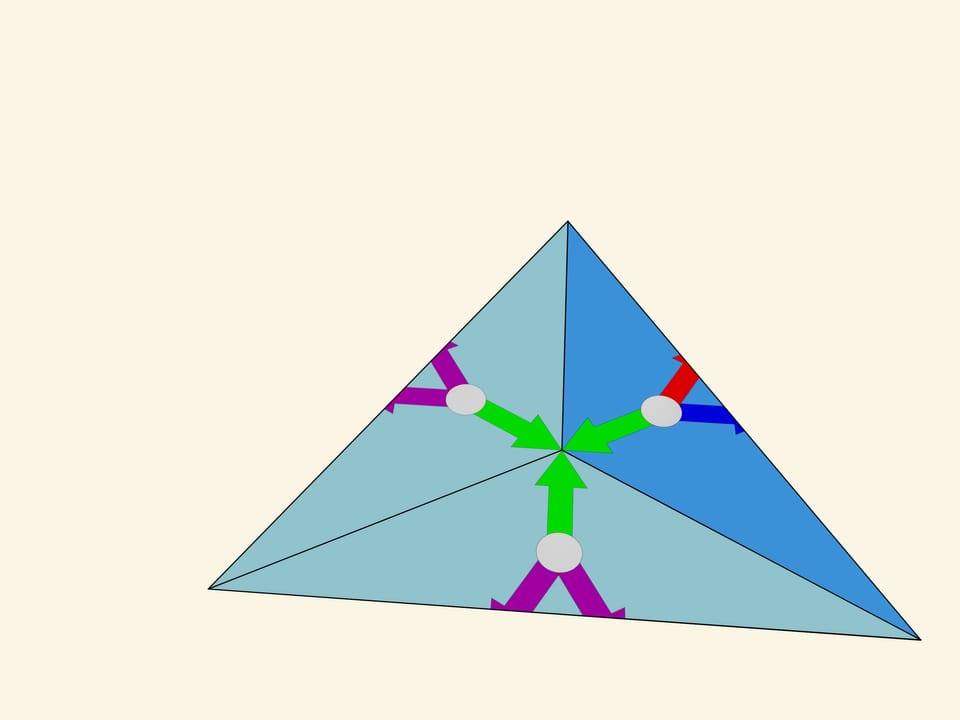
Рассмотрим треугольник с углами $120^\circ$—$30^\circ$—$30^\circ$. По своим геометрическим характеристикам этот треугольник вроде подходит, отражения относительно сторон дают замощение плоскости. Но начнём отражать… Внимательный зритель может заметить, что уже в отражениях первого порядка — относительно сторон самого фундаментального треугольника — присутствует нестыковка. Образы, полученные отражениями относительно сторон, прилегающих к углу в $120^\circ$, не симметричны друг другу. Таким образом, получающееся при математическом построении изображение зависит от последовательности, в какой производятся отражения. Точнее, если учитывать всевозможные отражения, то изображение будет являться «суммой» изначальной картинки и ее зеркальной копии.
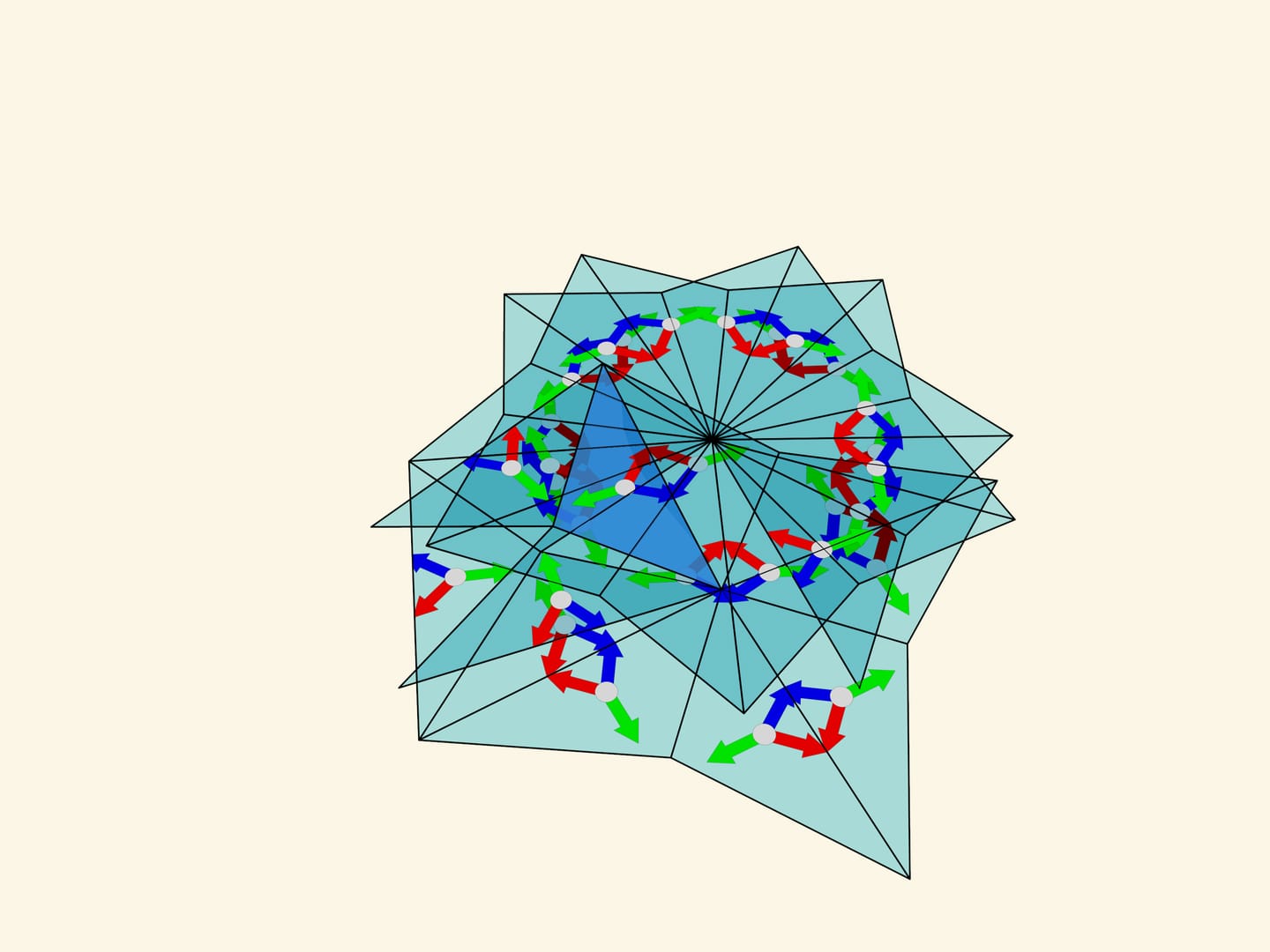
Сюрпризы, преподносимые треугольником с углами $120^\circ$—$30^\circ$—$30^\circ$, на этом не заканчиваются. Если изготовить калейдоскоп с такими углами, то на первый взгляд кажется, что в отличие от математического построения, говорящего что картинка будет, хоть и хорошо, но накладываться, полученная оптическая система, даёт красивую картинку. Однако это не так. Можно заметить, что даже выбранная нами простейшая картинка в виде разноцветных стрелочек, перпендикулярных зеркалам, отражается неодинаково даже при небольших порядках отражений. Где-то ближайшими к центрам образовавшихся шестиугольников видны стрелочки одного цвета, а где-то — другого. Если отойти подальше от фундаментального треугольника, то начинают встречаться и другие неприятности. Так что реальная картинка не совпадает с предсказанной математически. Дело в том, что изображение формируется в каждом из зеркал раздельно по уже указанному принципу «образ зеркала в зеркале, снова работает как зеркало». Но изображение, формирующееся в одном из зеркал, не переотражается в другом зеркале.
Если покачать калейдоскоп, построенный на фундаментальном треугольнике с углами $120^\circ$—$30^\circ$—$30^\circ$, то видно, что картинка зависит от взаимного расположения наблюдателя и оси калейдоскопа — при покачивании изображение меняется около ребра зеркальной призмы.
В случае же произвольного треугольника, если начать делать всевозможные его отражения на плоскости, они будут накладываться друг на друга, и ни о каком красивом изображении говорить не приходится. При построении оптической системы в виде зеркальной призмы над таким треугольником общее изображение будет складываться из как-то перемешанных обломков изначального изображения и не будет регулярным.
Итак, калейдоскоп можно построить, используя в качестве основания призмы треугольник с углами $60^\circ$—$60^\circ$—$60^\circ$, $90^\circ$—$45^\circ$—$45^\circ$ или $90^\circ$—$30^\circ$—$60^\circ$. Как математически понять, что треугольник с углами $120^\circ$—$30^\circ$—$30^\circ$, подходящий геометрически для замощения плоскости с использованием симметрий, не подходит для построения калейдоскопа? Все ли возможные треугольники уже перечислены?
Описанные условия на получающееся в калейдоскопе изображение можно сформулировать более точно: треугольник в основании должен иметь углы $\frac{180^\circ }{k}$, $\frac{180^\circ}{m}$, $\frac{180^\circ}{n}$, где $k$, $m$, $n$ — натуральные числа, причём $\frac{180^\circ}{k}+\frac{180^\circ}{m}+\frac{180^\circ}{n}=180^\circ$. Если не учитывать порядок, то единственными решениями $\{k, m, n\}$ этого уравнения являются тройки $\{3, 3, 3\}$, $\{2, 4, 4\}$ и $\{2, 6, 3\}$, дающие уже хорошо знакомые наборы углов $60^\circ$—$60^\circ$—$60^\circ$, $90^\circ$—$45^\circ$—$45^\circ$ и $90^\circ$—$30^\circ$—$60^\circ$. Других «калейдоскопных» треугольников не бывает.
Если в основании зеркальной призмы использовать не треугольник, а произвольный многоугольник, то правильный калейдоскоп получается ещё лишь при использовании четырёх зеркал, поставленных по сторонам прямоугольника.
Приведённые рассуждения о принципе устройства калейдоскопа являются началом очень интересной области математики — теории групп, порождённых отражениями.
Литература
Винберг Э. Б. Калейдоскопы и группы отражений // Математическое просвещение. Серия 3. — 2003. — Вып. 7. — С. 45—63.
Смотри также
Калейдоскоп // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 150—153.
Группа диэдра // Математические этюды.
Футбольный мяч: зеркальный икосаэдр // Математические этюды.