Живя на поверхности Земли, люди долгое время считали, что она плоская. Понадобилось построение научных теорий, чтобы догадаться, что Земля похожа на шар. И лишь во второй половине XX века люди смогли посмотреть на Землю из объемлющего пространства и убедиться воочию.
Так же и в математике: выйдя в объемлющее пространство, зачастую можно узнать много интересного об объекте.
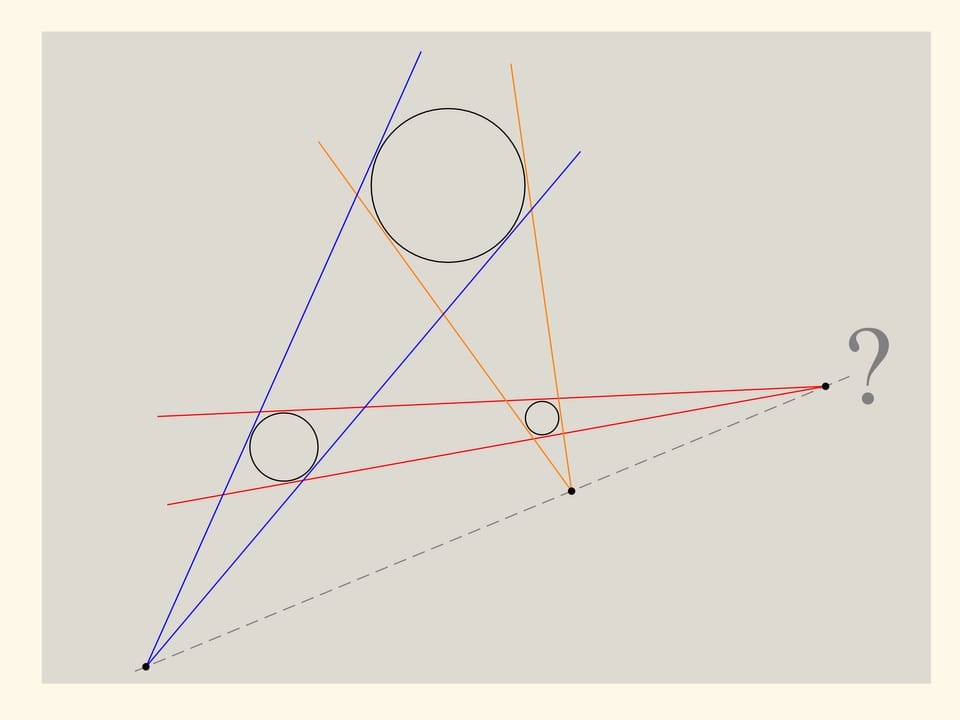
Рассмотрим три произвольные окружности и проведём попарные касательные к каждой паре окружностей. Что можно сказать о полученных трёх точках, являющихся пересечением касательных, проведённых к двум окружностям? Судя по рисунку, они лежат на одной прямой. Однако рисунок — это не доказательство, а лишь информация для выработки гипотезы. Попробуем её доказать.
Рассматриваемая задача и рисунок к ней расположены на плоскости. Давайте посмотрим на эту плоскость извне — из объемлющего трёхмерного пространства.
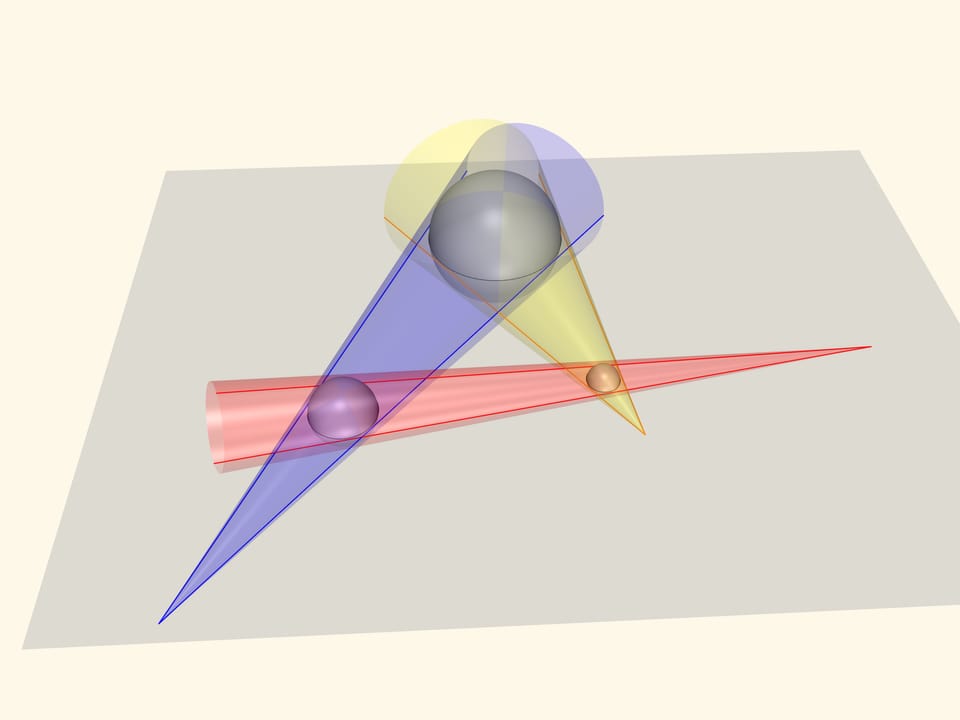
Построим три сферы, чьими экваторами являются изначальные окружности. Конусы, попарно охватывающие сферы, в качестве образующих будут иметь касательные, рассматриваемые в задаче. Точки, которые по нашей гипотезе лежат на одной прямой, будут вершинами конусов.
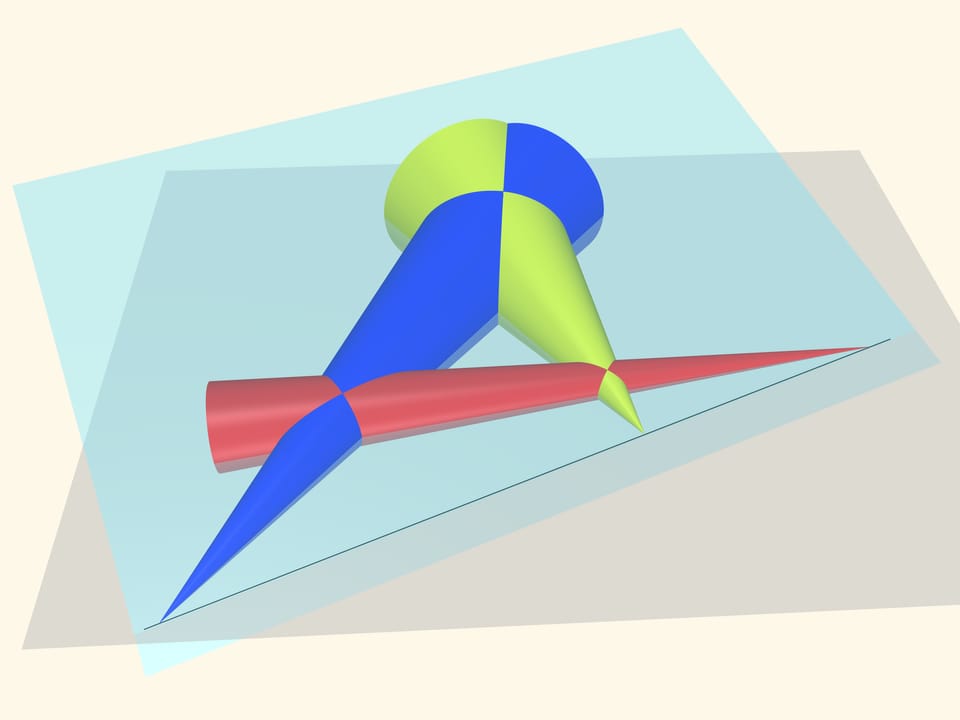
Положим на конусы плоскость. Интересующие нас точки — вершины конусов — принадлежат этой плоскости, так же, как и изначальной — «экваториальной» плоскости. А две (непараллельные) плоскости пересекаются по прямой! Значит, действительно, как и было предположено, эти три точки — точки пересечения попарных касательных к трём произвольным окружностям — лежат на одной прямой.
Эта теорема носит имя французского математика и государственного деятеля Гаспара Монжа. Предложенное рассуждение доказывает её в случае, когда на три шара, построенных на окружностях, можно положить плоскость. Придумайте пример трёх окружностей, для которых это сделать нельзя, а уточнение доказательства в этом случае посмотрите в статье Владимира Юрьевича Протасова.
Литература
Протасов В. Ю. Выход в пространство — 2 // Журнал «Квант». 2017. № 12. Стр. 7—11; 2018. № 1. Стр. 8—14; 2018. № 2. Стр. 2—6.
Шарыгин И. Ф. Выход в пространство // Журнал «Квант». 1975. № 5. Стр. 45—49.