Будем проводить измерения. Но всегда, прежде чем что-то мерить, надо определиться с единицей измерения, которая будет использоваться. Помните: «А в попугаях-то я гор-р-р-аздо длиннее...»?
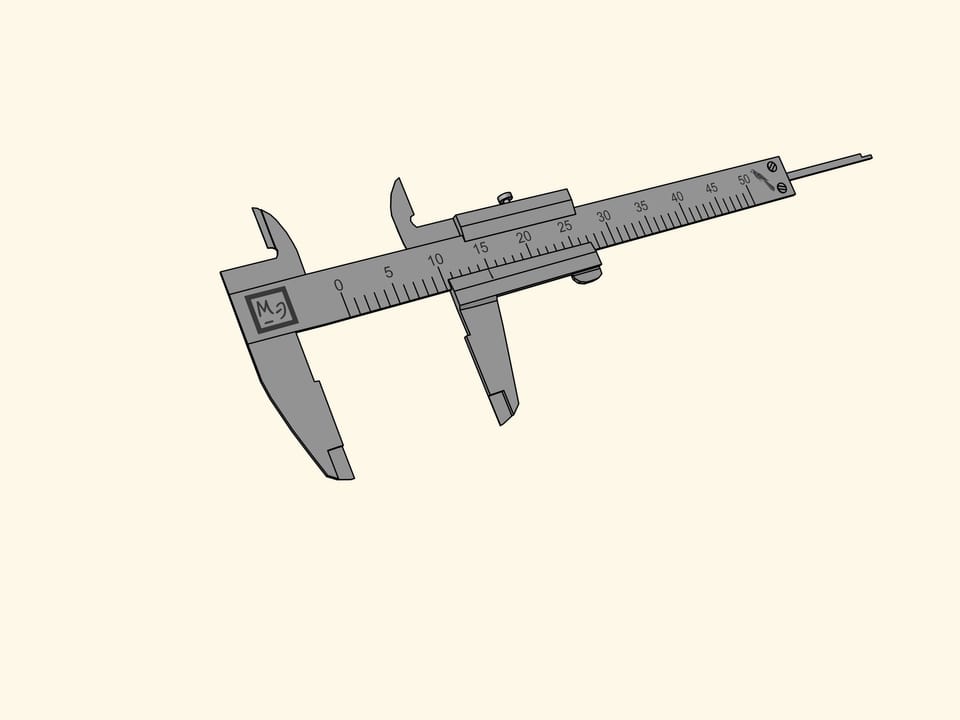
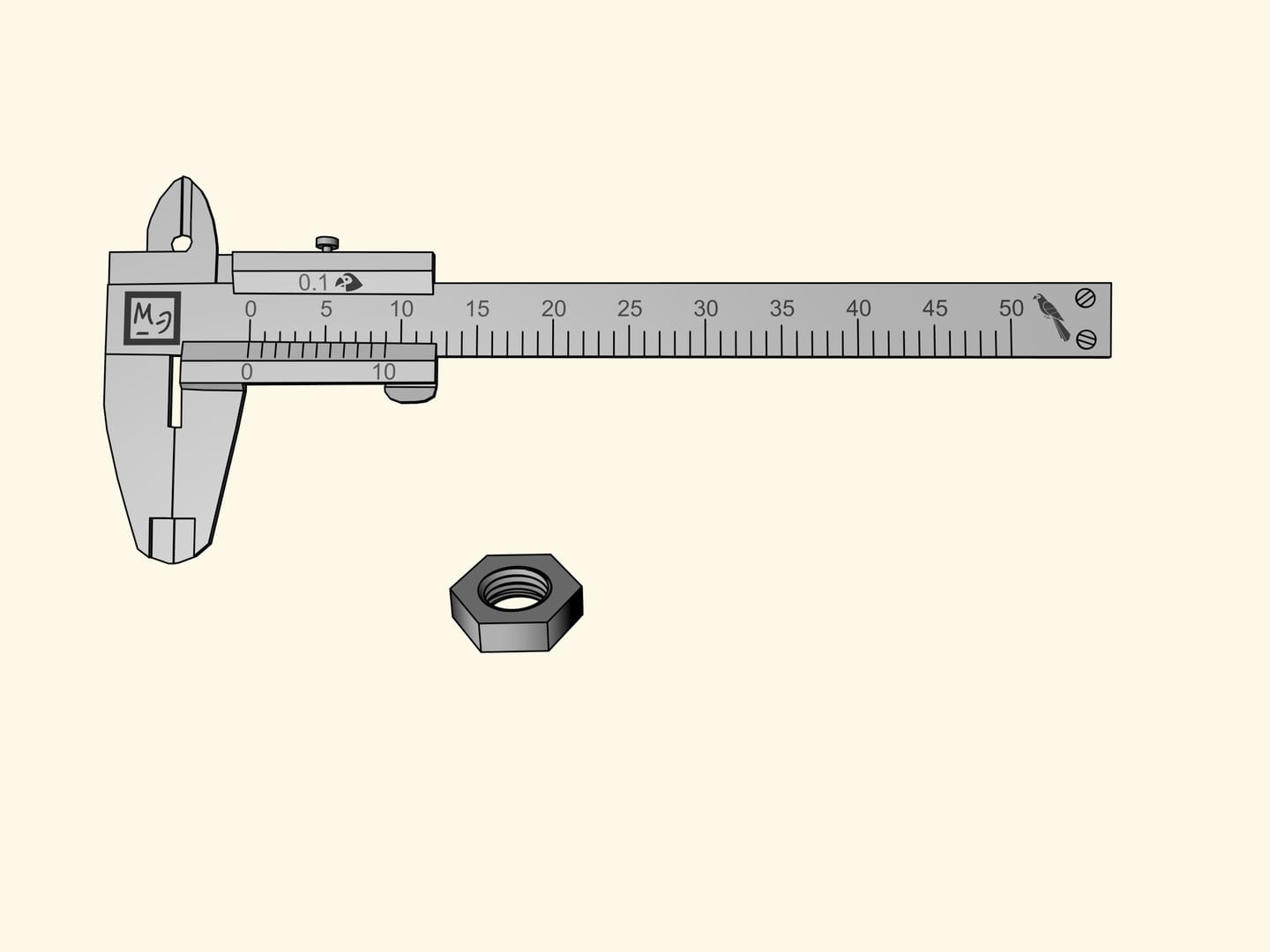
Сколько размеров, равных 15 попугаям, отмерено штангенциркулем? Губки для наружных измерений, расположенные снизу от штанги, отмеряют внешний размер предмета, например, внешний диаметр трубы. Губки для внутренних измерений, находящиеся сверху от штанги, используются для измерения, например, внутреннего диаметра трубы. А торчащий хвостик — линейка глубинометра — применяется для измерения глубин отверстия. Все три величины при таком положении подвижной рамки равны 15 попугаям.
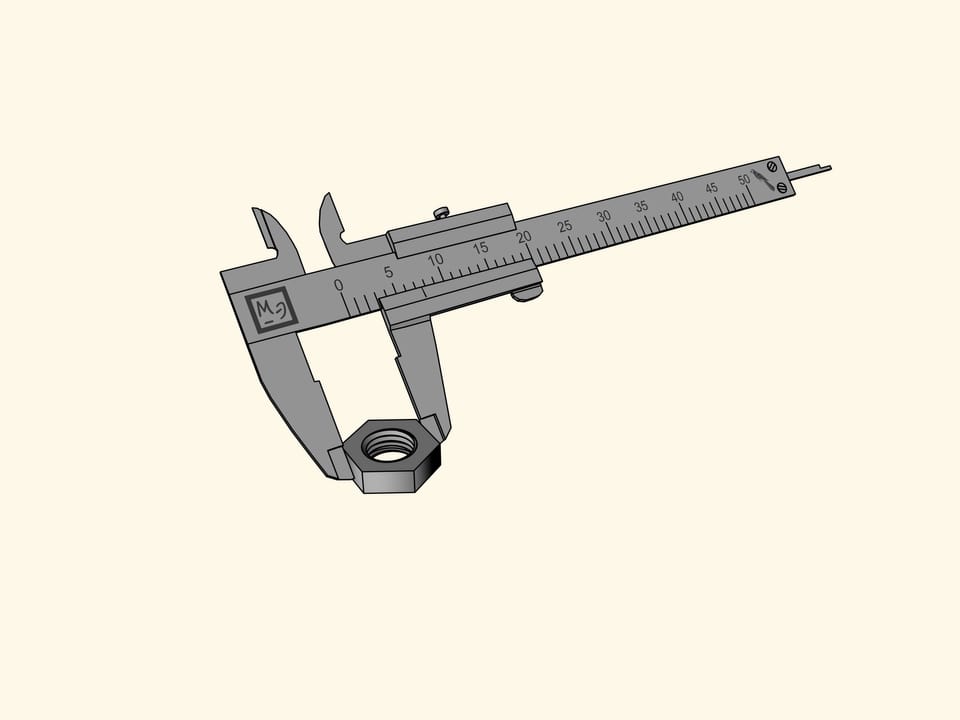
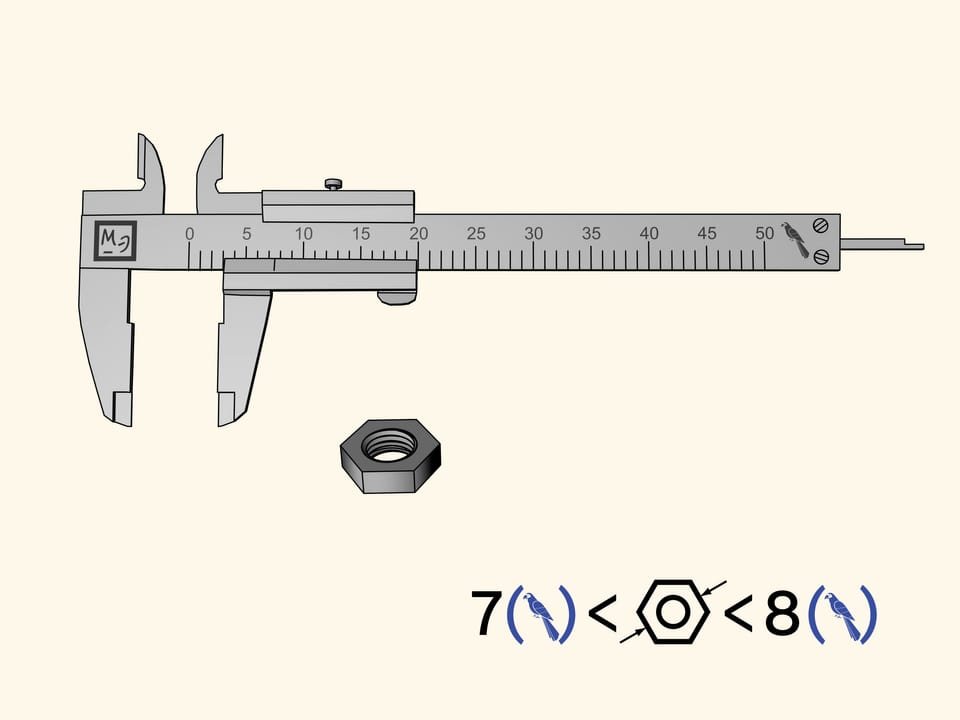
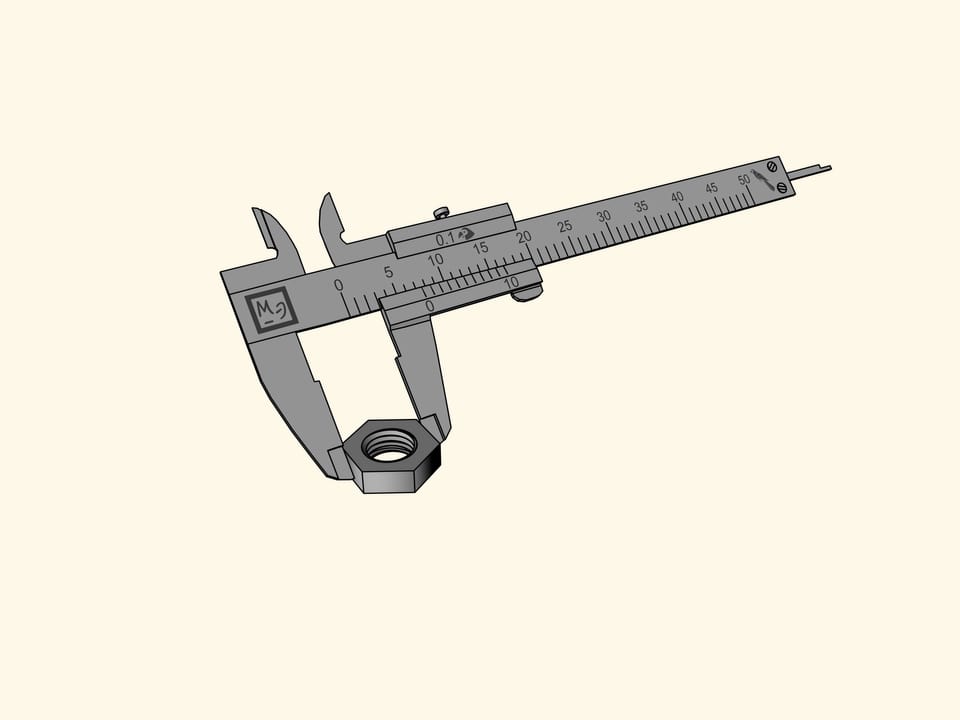
Измерим шестиугольную гайку. Неудачно — рисочка на подвижной рамке, показывающая размер, попала между делениями верхней шкалы. Всё, что можно сказать при измерении таким инструментом: размер гайки больше семи попугаев, но меньше восьми. Более точно определить на глаз сложно.
Идея, не усложняющая само устройство штангенциркуля, но при этом позволяющая получать более точные результаты, была придумана несколько веков назад. Она заключается в нанесении на подвижную рамку специальной дополнительной шкалы — нониуса.
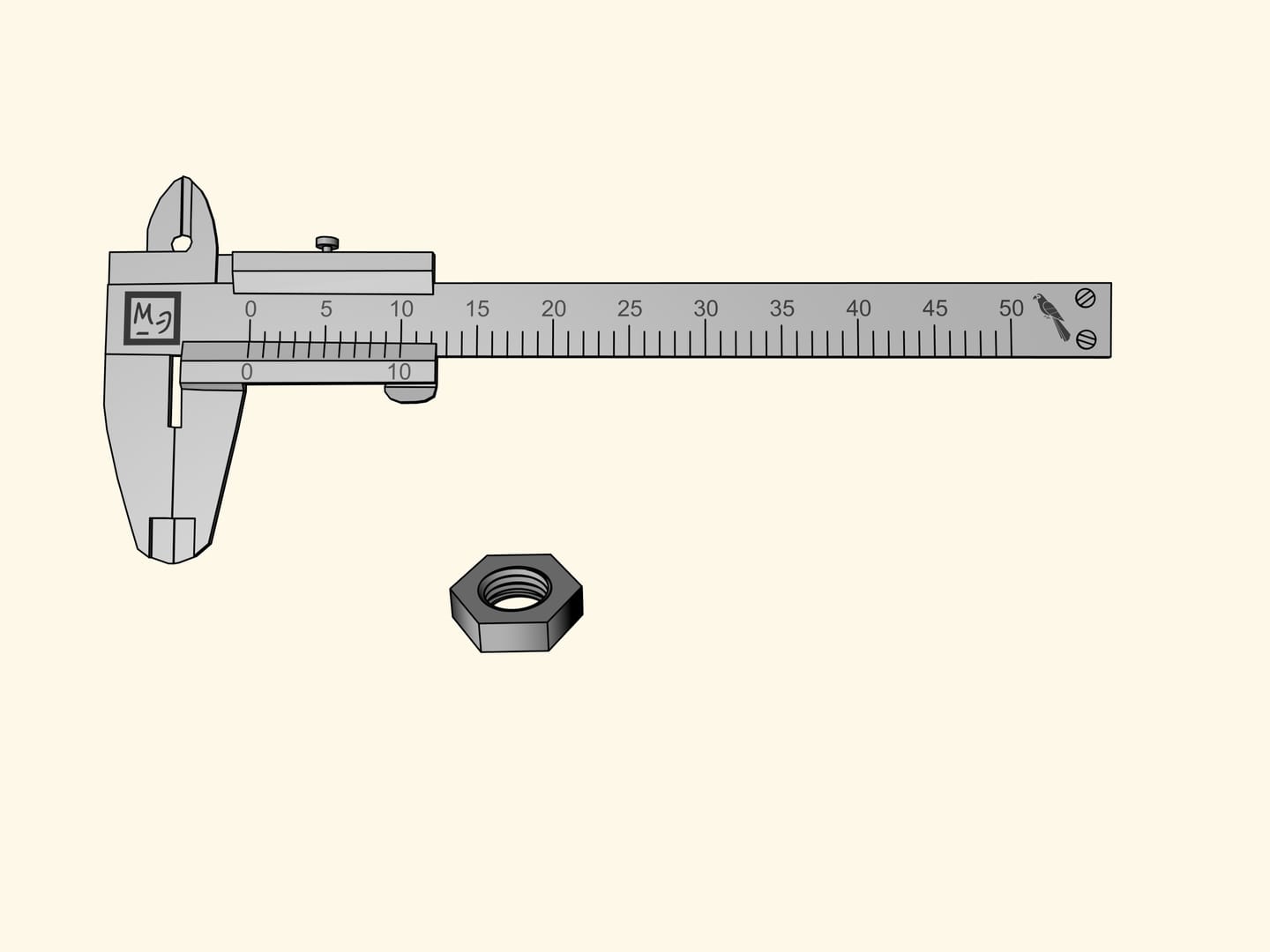
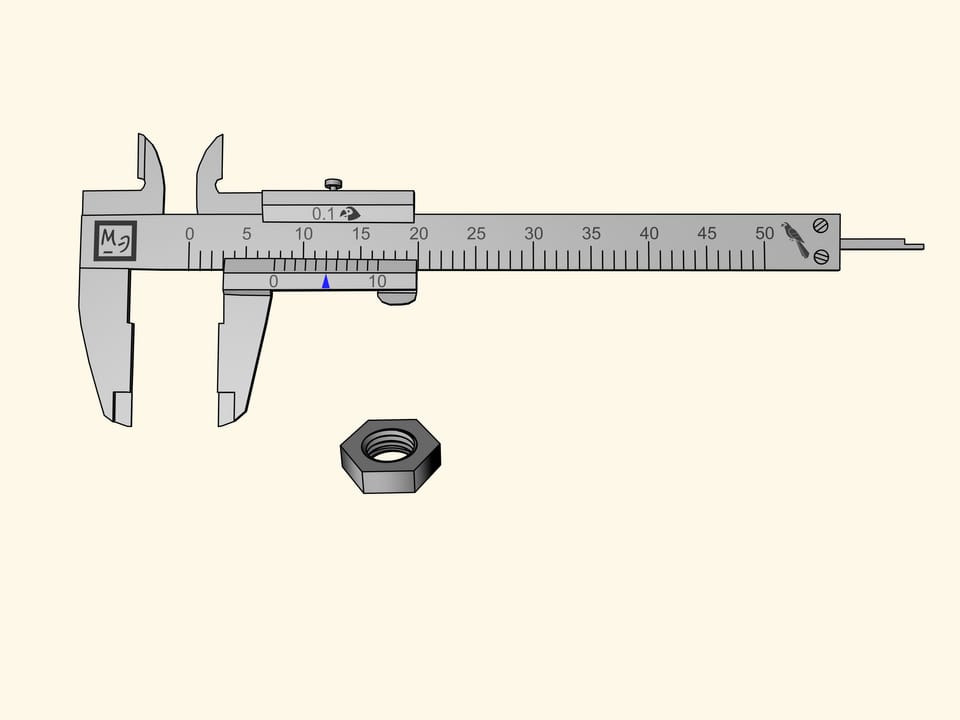
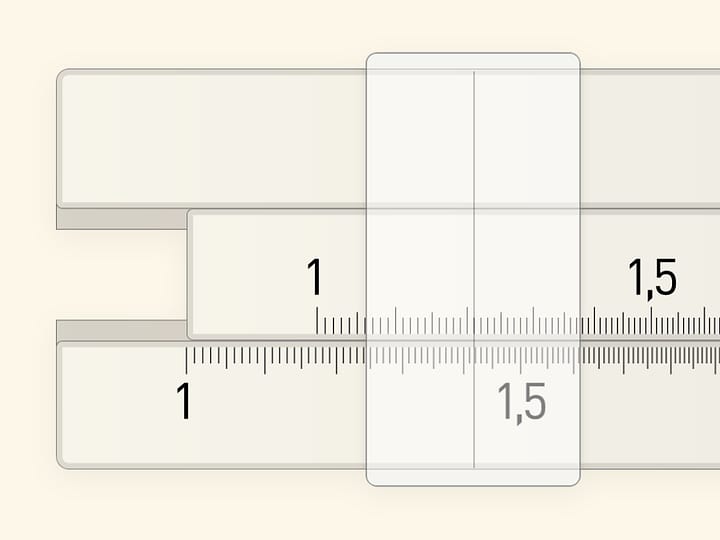
Нанесём на подвижную рамку 10 дополнительных к нулевому делений, совпадающих с делениями шкалы штанги. А теперь равномерно сожмём эти 10 делений так, чтобы они укладывались в 9 делений основной шкалы. Шкала, построенная по такому принципу, и называется нониус — в честь португальского математика П. Нуниша, придумавшего сам принцип. А современный вид был предложен французским математиком П. Вернье, и поэтому второе название этой шкалы — верньер.
Оказывается, построенная таким образом дополнительная шкала позволяет измерять уже с точностью до 0,1 попугая! Но каким образом?
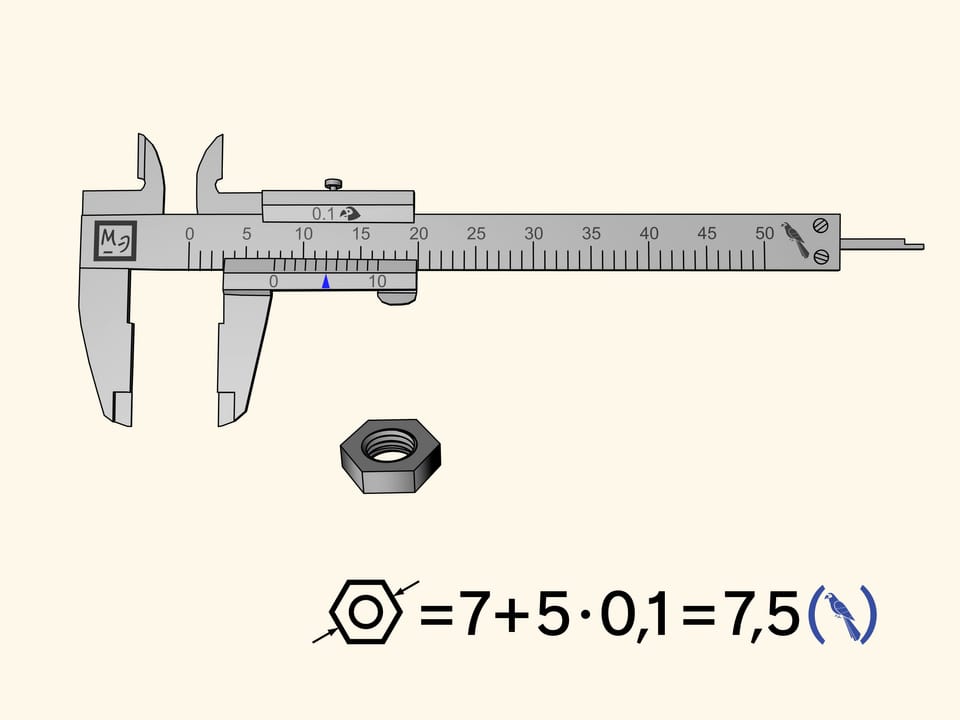
Измерим гайку ещё раз. Нулевая отметка нижней шкалы будет, как и раньше, между седьмым и восьмым делениями. Значит, полных семь попугаев в нашем размере содержится. Теперь давайте пробежим по делениям дополнительной шкалы слева направо и будем искать то деление, которое совпадёт с каким-нибудь делением основной шкалы. В нашем случае это пятое деление. Значит, размер гайки равен $7 + 5 × 0{,}1 = 7{,}5$ (попугаев).
Попробуйте математически обосновать приведённое выше рассуждение. Подумайте, как с помощью похожей идеи добиться большей точности измерений.
Смотри также
Измерение штангенциркулем // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 82—83.