На листе бумаги нарисовали произвольный многоугольник. Можно ли так сложить лист бумаги, чтобы вырезать многоугольник одним прямолинейным разрезом?

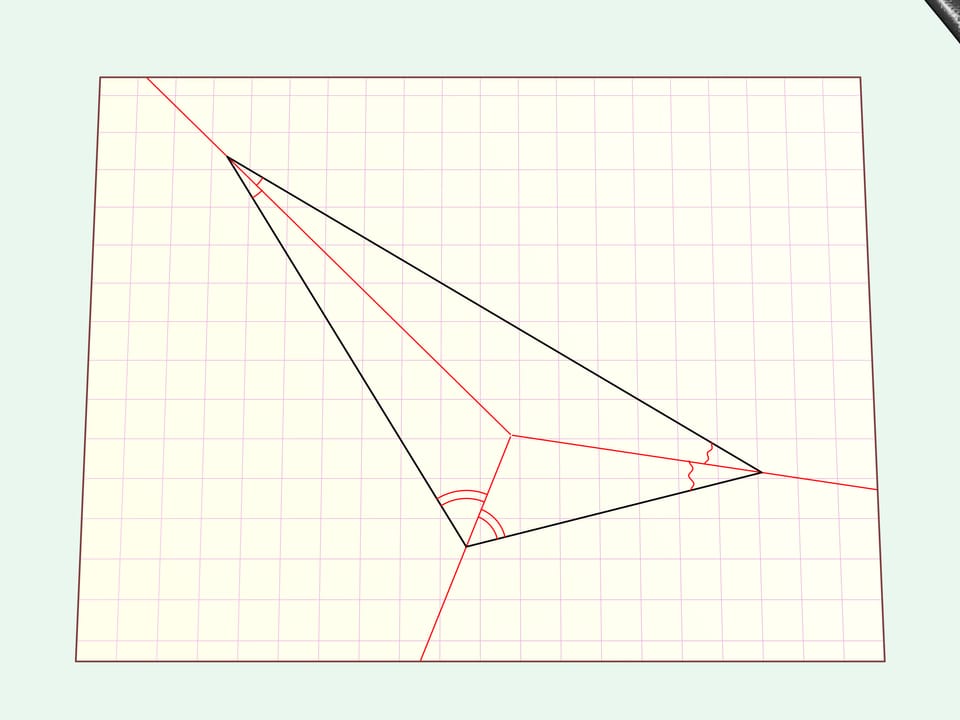
Рассмотрим простейший случай — произвольный треугольник.

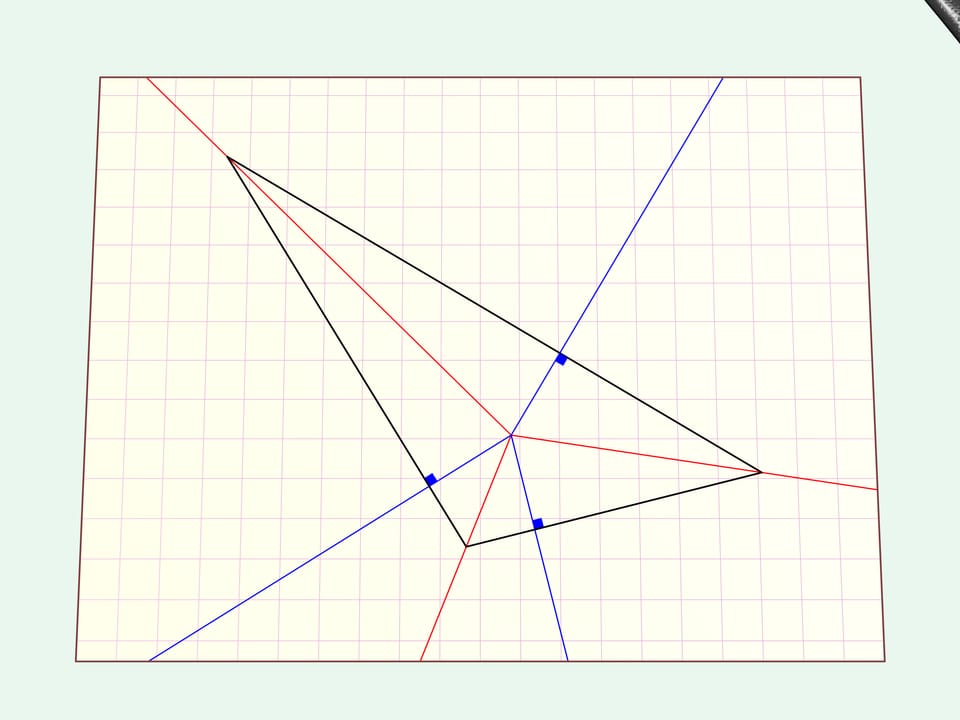
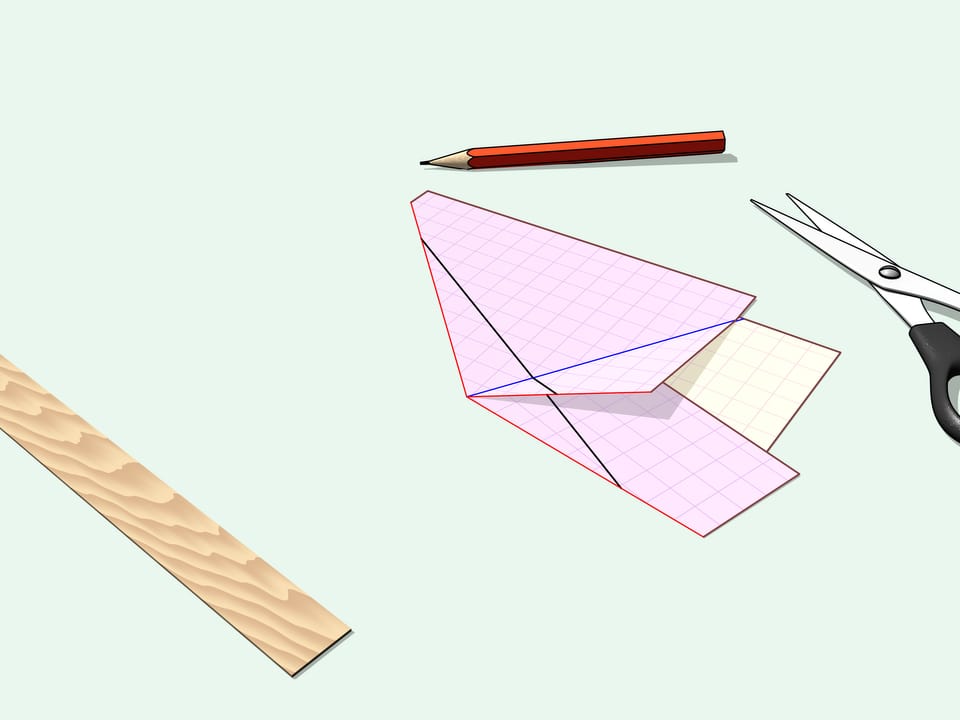
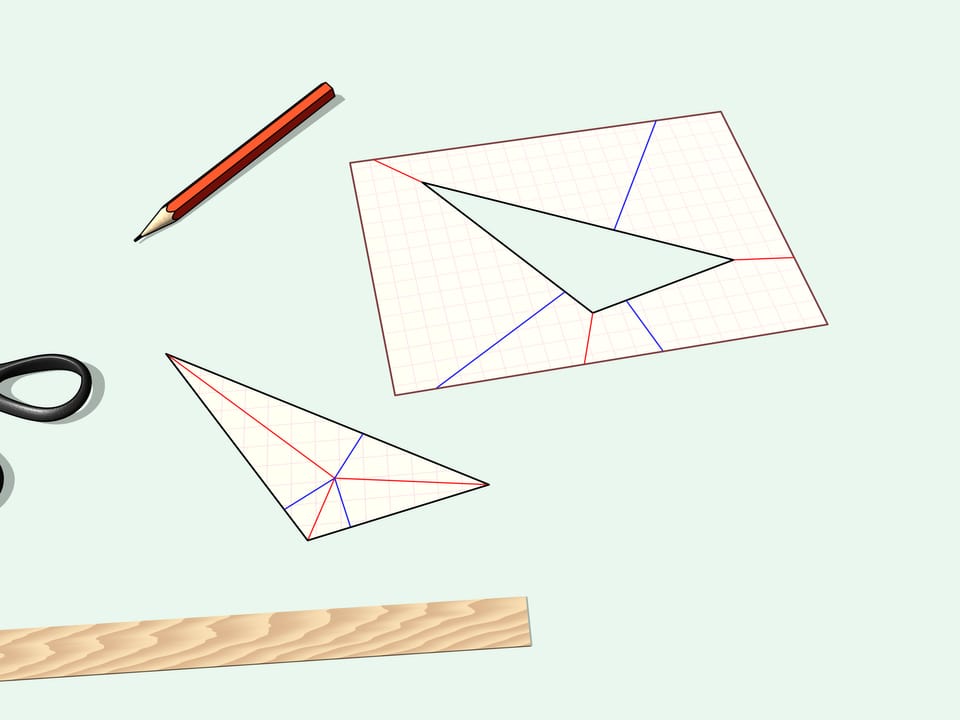
Проведём биссектрисы и из точки их пересечения опустим перпендикуляры на стороны треугольника. По этим лучам и будем сгибать лист бумаги. Все границы треугольника — стороны — оказались лежащими на одной прямой. Сделаем вдоль неё прямолинейный разрез.

Развернём отрезанный уголок — это наш изначальный треугольник. Если развернуть оставшуюся часть листа, то видно, что ничего лишнего не вырезано — дырка тоже имеет вид изначального треугольника.

Нарисуем пятиконечную звезду. Это невыпуклый многоугольник с 10 вершинами. Однако в этом случае задача облегчается симметричностью звезды. Проведём лучи, исходящие из центра и проходящие через вершины. По этим лучам сложим лист бумаги. Отрежем уголок. После разворачивания получим вырезанную звезду и дырку в виде звезды.

Многоугольник, нарисованный в начале фильма, тоже может быть вырезан одним прямолинейным разрезом. В 1998 году была доказана общая