Орбита спутника носит название геостационарной, если при вращении Земли спутник всегда висит над одной и той же точкой емной поверхности. Такие орбиты зачастую используются в системах связи и позиционирования.
Спутник, который Вы видите на картинке, является символом космической программы нашей страны. Это «СОЮЗ-ТМ».
А вот так в какой-то момент выглядела заставка программы «Время» — основной информационной телепрограммы страны.
Ну а в мультфильме мы посмотрим, как происходит процесс передачи сигнала, например, современного спутникового телевидения.
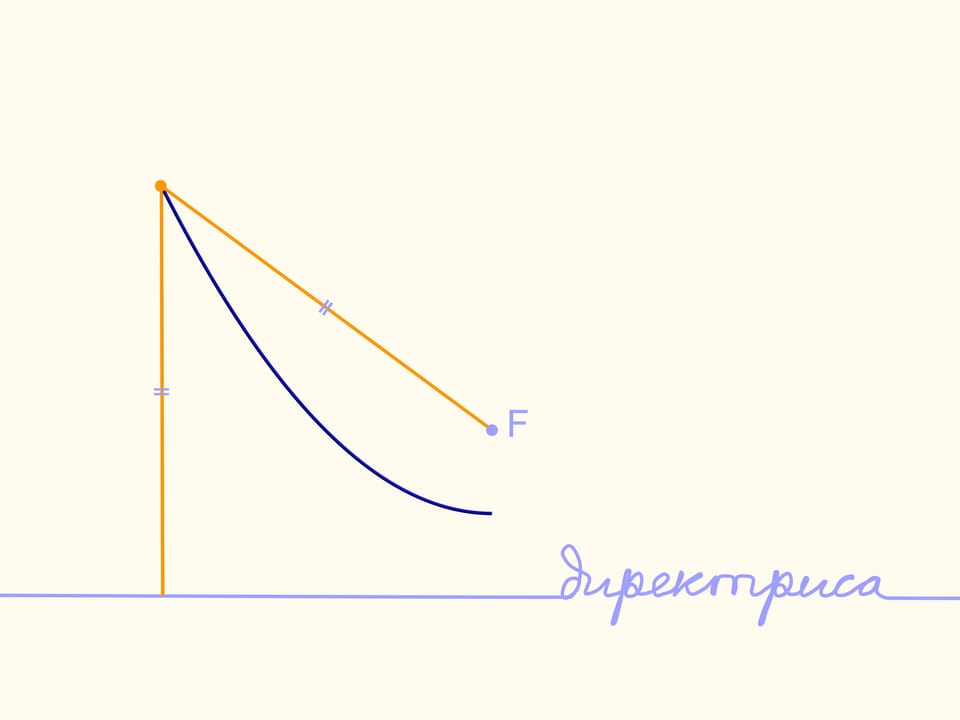
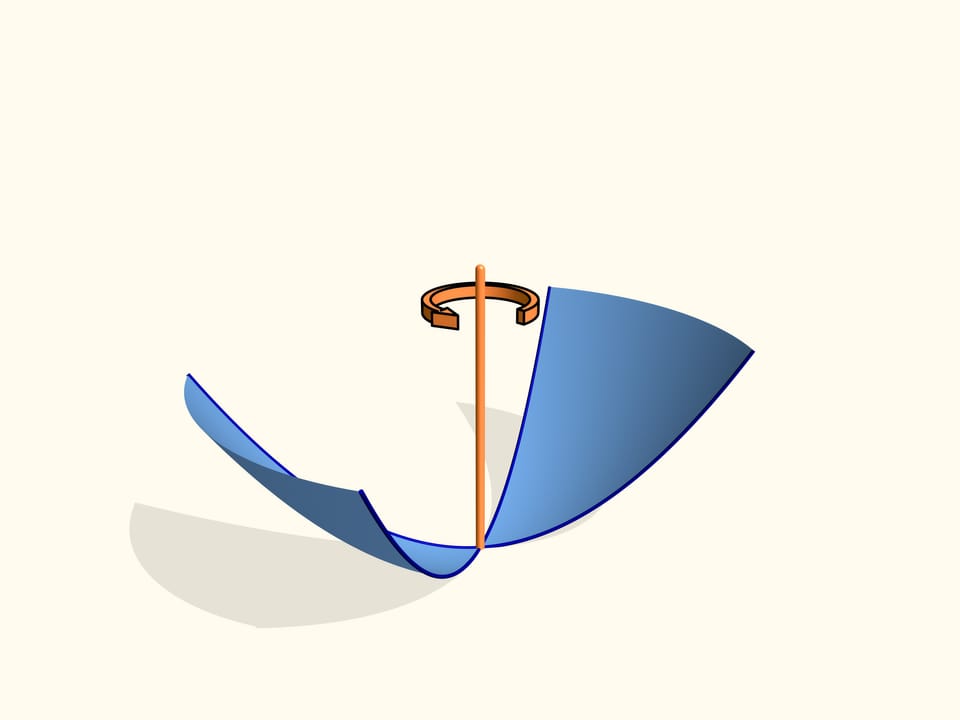
Проведём прямую и назовём её директрисой. Возьмём точку вне неё. Геометрическое место точек, равноудалённых от директрисы и данной точки (фокуса), называется параболой.
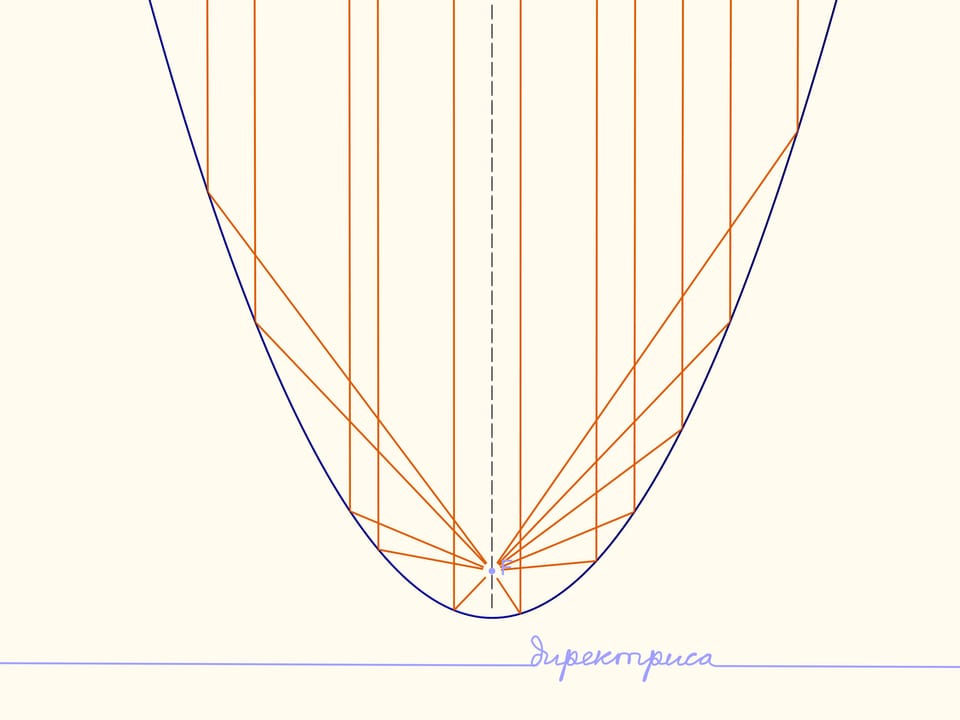
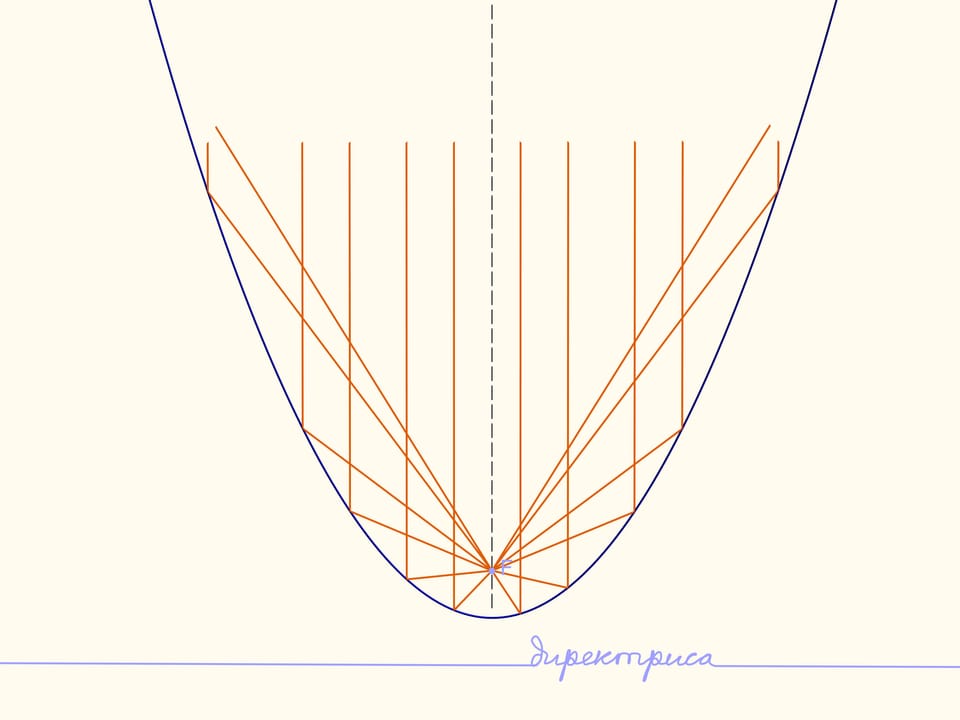
Если направить на параболу лучи света, параллельные её оси симметрии, то все лучи соберутся в фокусе параболы. Это свойство называется оптическим свойством параболы.
Верно и обратное. Если поместить лампочку в фокус, то лучи, отразившись от параболы, пойдут параллельно, причём граница света будет прямой.
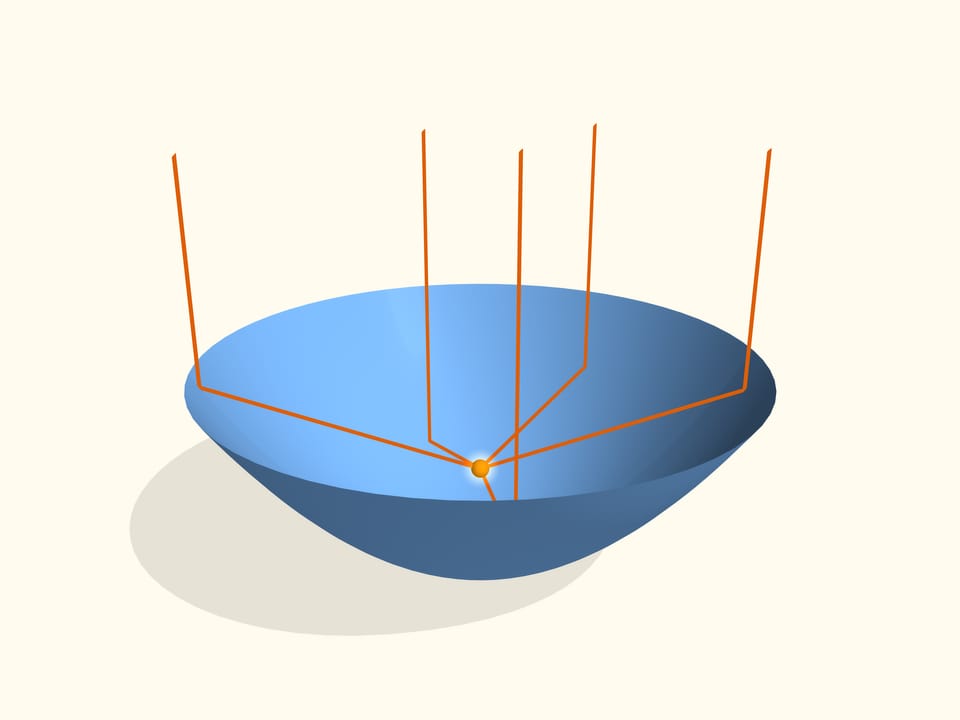
Если провращать параболу относительно её оси симметрии, то получится уже поверхность вращения второго порядка — параболоид. Так как в любом сечении плоскостью, содержащей ось симметрии, получается одна и та же парабола, то оптическое свойство верно и для параболоида. Если поместить лампочку в фокус параболоида, то лучи, отразившись от поверхности, пойдут параллельно друг другу. Обратное тоже верно.
Именно это свойство используется в спутниковых параболических антеннах. Так как спутник находится очень далеко от антенны, то лучи можно считать почти параллельными, и приёмник сигнала ставится в фокус параболоида.
На латыни focus означает «очаг, огонь». Как математический термин слово «фокус» ввёл Иоганн Кеплер в сочинении «Оптическая астрономия» (1604).
Смотри также
Параболическая антенна // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 46—47, 297—302.