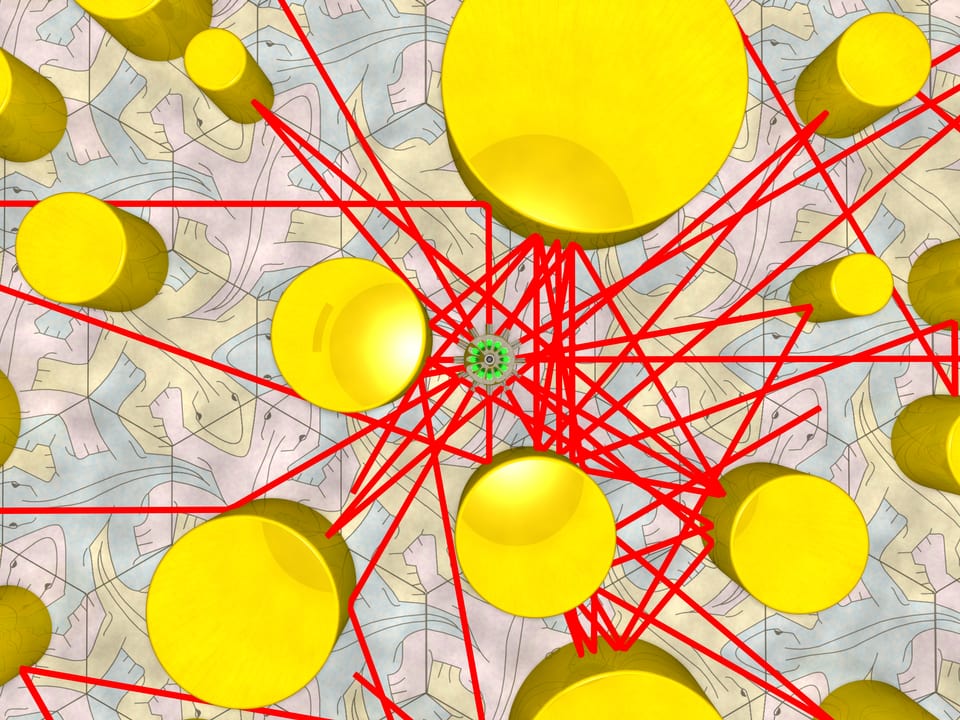
Можно ли так расставить круглые зеркальные колонны, чтобы луч, идущий параллельно полу, не достигал стены ни при каком изначальном направлении? Колонны с зеркальной цилиндрической боковой поверхностью могут быть произвольного диаметра и поставлены в любую точку с условием, что они не касаются друг друга (в таком случае задача тривиальна).
Как известно, отражение от зеркала происходит по правилу «угол падения равен углу отражения». В случае, если зеркало неплоское, то углом между лучом и поверхностью зеркала называется угол с касательной плоскостью, проведённой в точке падения луча.
Сколько достаточно колонн и каково должно быть их расположение, чтобы луч был экранирован и не достиг стенки? Хватит конечного числа зеркал или их нужно бесконечно много? А может, и бесконечного числа не хватит?
Понятно, что одной колонны не хватит. Луч может пройти мимо неё, но даже если он и попадёт в колонну, то после отражения всё равно достигнет стены. Таким образом, при любом начальном направлении луч падает на стену.
Очевидно, что и двух, и трёх колонн недостаточно — из центра зала по некоторым направлениям будет видна стена. И значит, луч, пущенный в этих направлениях, достигнет её.
Интуиция подсказывает, а эксперимент подтверждает, что малого количества колонн недостаточно для экранирования луча.
Поставим много колонн и выпустим лучи «во всех» направлениях. Эксперимент показывает, что лучи достигнут стены.
Однако эксперимент — это ещё не доказательство. Может быть, надо было расставить колонны как-то по-другому или же взять на несколько колонн больше… До сих пор математики не знают, достаточно ли какого-либо конечного количества (пусть и очень большого) колонн для экранирования луча. Если достаточно, то каковы должны быть их диаметры и расположение? А может быть, и бесконечного числа колонн не хватит для решения поставленной задачи?
Быть может, вы придумаете, как нужно расставить колонны?