Что такое развёртка многогранника? Вы скажете — кусок картона, из которого можно свернуть данный многогранник. В этом есть правда, но это не вся правда. Оказывается, понятие развёртки включает в себя больше, чем просто кусок картона.
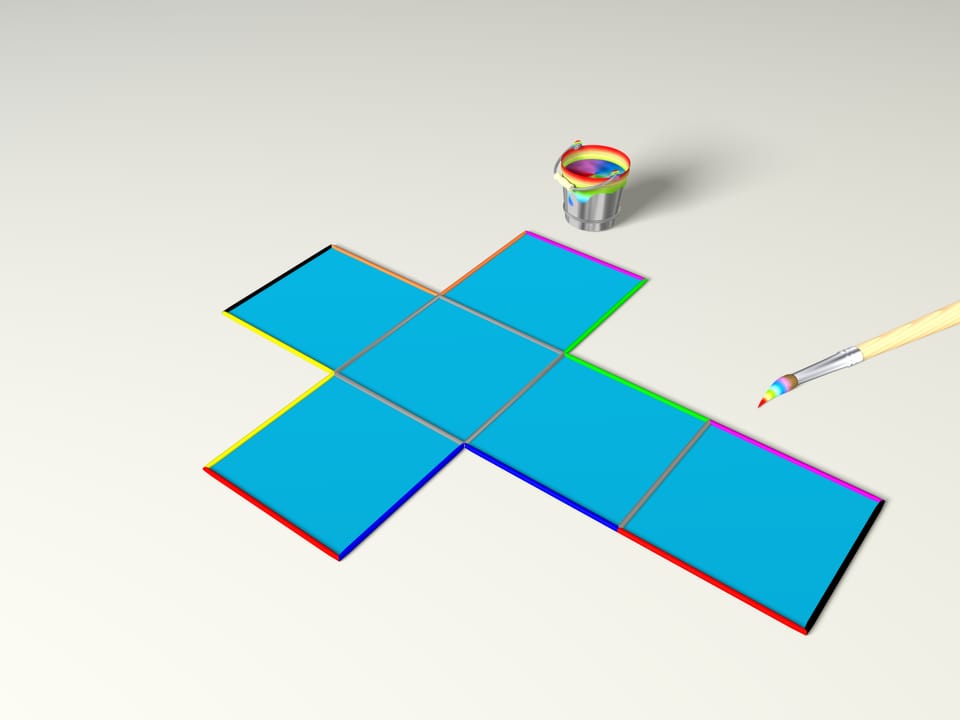
Какой многогранник можно свернуть из столь хорошо известного латинского креста? Конечно же, куб. Для этого надо покрасить ребра, как это сделала наша волшебная кисточка (рёбра одинакового цвета склеиваются в многограннике друг с другом).
На самом деле, конечно же, лучше было бы раскрашивать не ребра, а каждую пару точек в один цвет. Это бы задало, как говорят в математике, условия склейки границ.
После того как условия склейки границ заданы, рёбра, проходящие внутри куска картона, определены однозначно по теореме А. Д. Александрова.
Итак, из креста можно сложить куб.
Но оказывается, что если условия склейки границ задать по-другому, то можно получить совсем даже не куб!
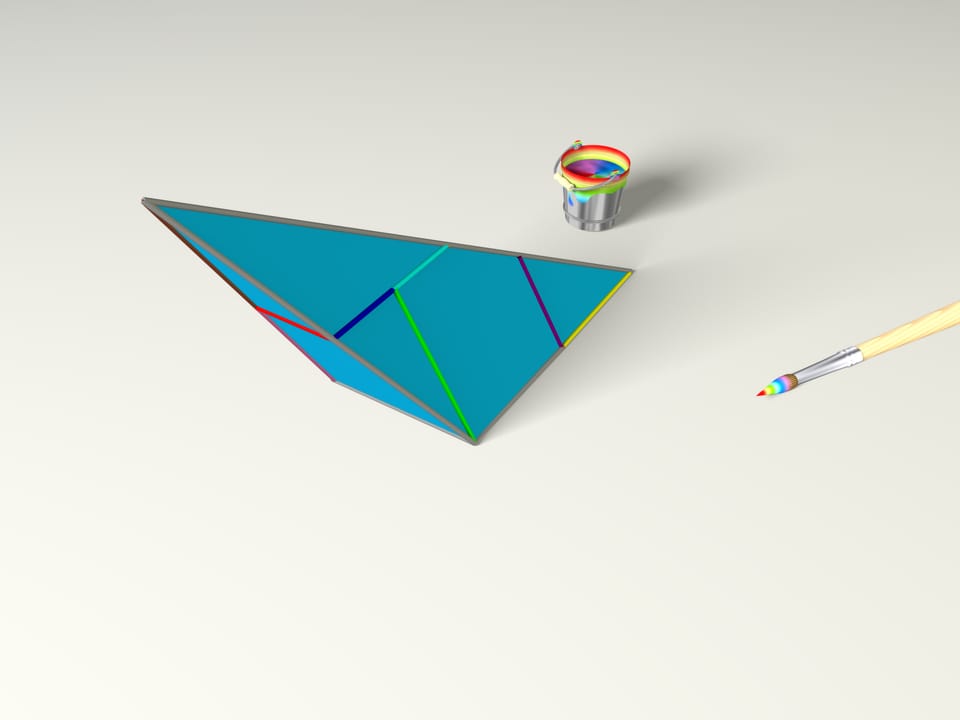
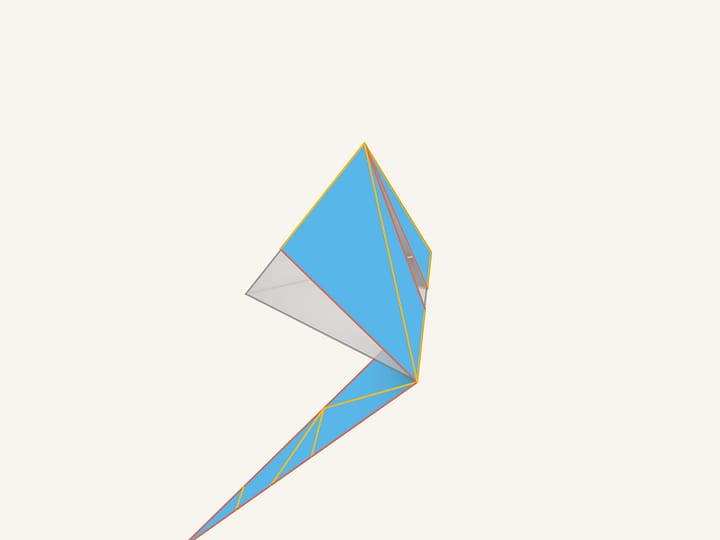
Наша волшебная кисточка покрасила границы вот таким образом. Ещё один её взмах — и мы уже знаем, как определены рёбра внутри куска картона. Если теперь, следуя нарисованным условиям склейки, сложить многогранник, то получим пирамиду!
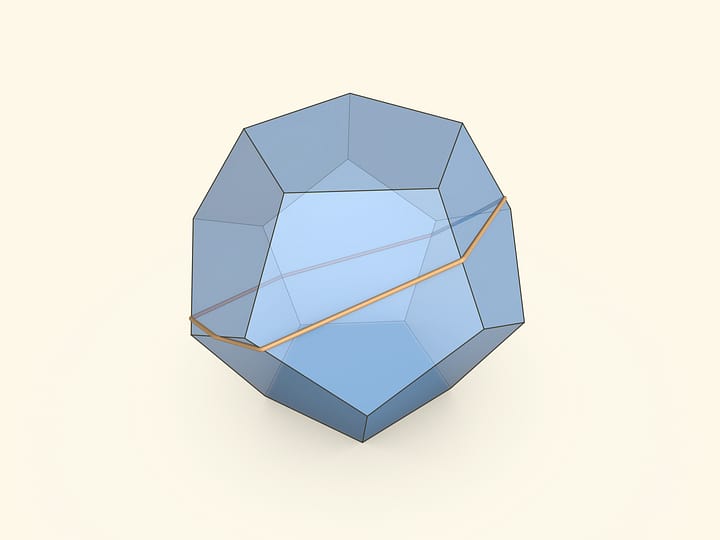
Не так давно было доказано, что по-разному задавая условия склейки границ латинского креста, из него можно сложить 5 различных типов выпуклых многогранников.
Итак, как мы убедились, в понятие развёртки входит не только кусок картона, но и условия склейки его границ. Если последнее не определено, то из одного и того же куска можно сложить разные выпуклые многогранники.
Литература
Александров А. Д. Выпуклые многогранники.
Anna Lubiw, Joseph O'Rourke. When Does a Polygon Fold to a Polytope.
Demaine E. 85 вариантов сложения латинского креста.
Долбилин Н. П. Три теоремы о выпуклых многогранниках.
Часть 1 // Квант. — 2001. — № 5. — С. 7—12.
Часть 2 // Квант. — 2001. — № 6. — С. 3—10.