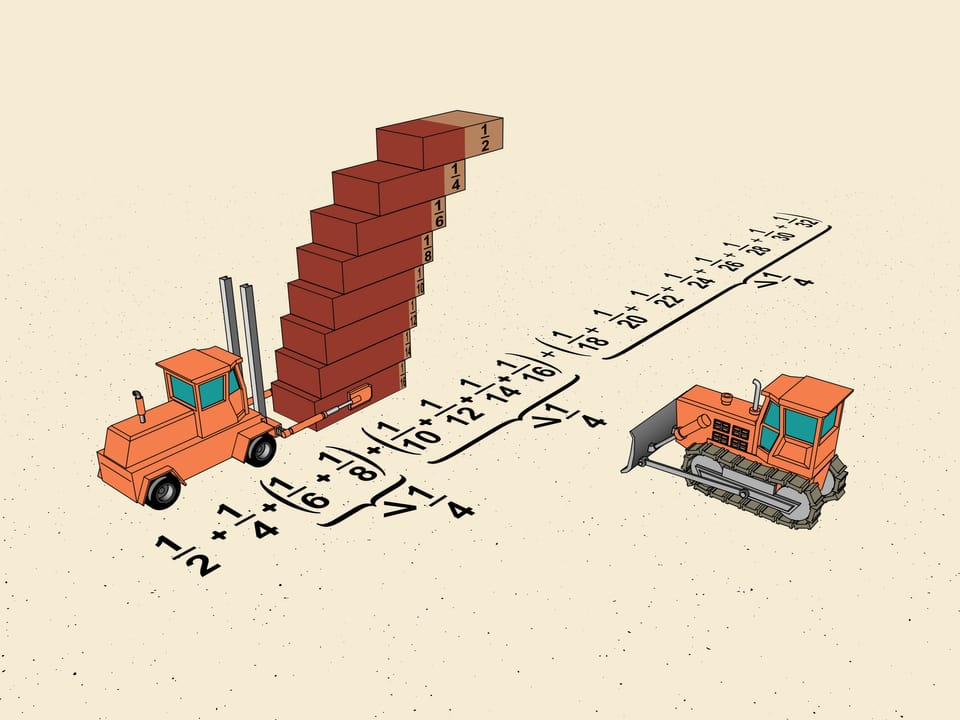
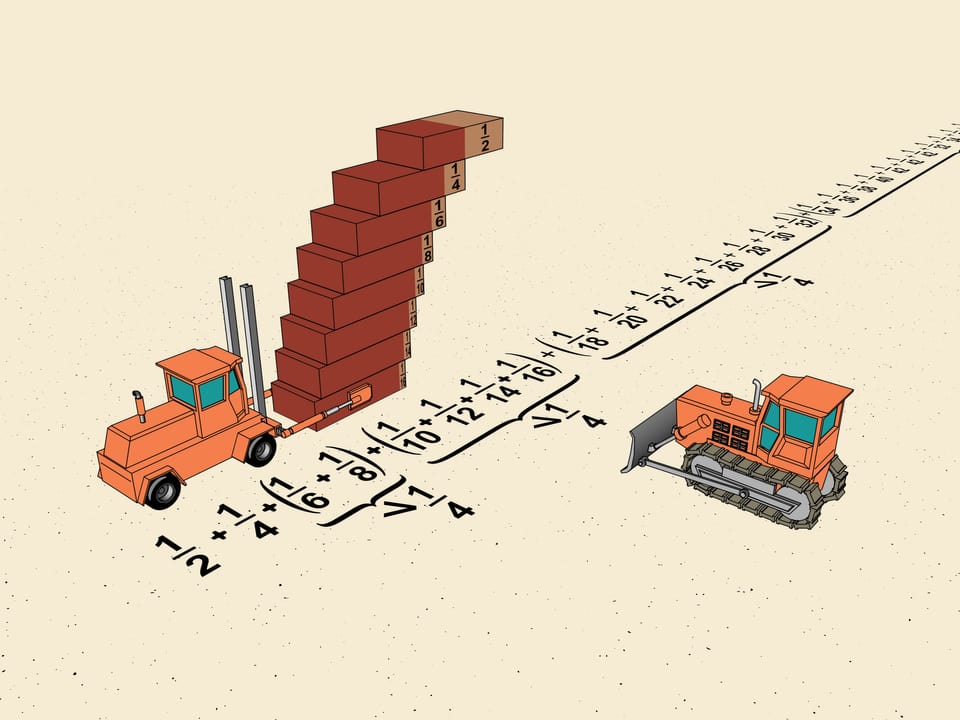
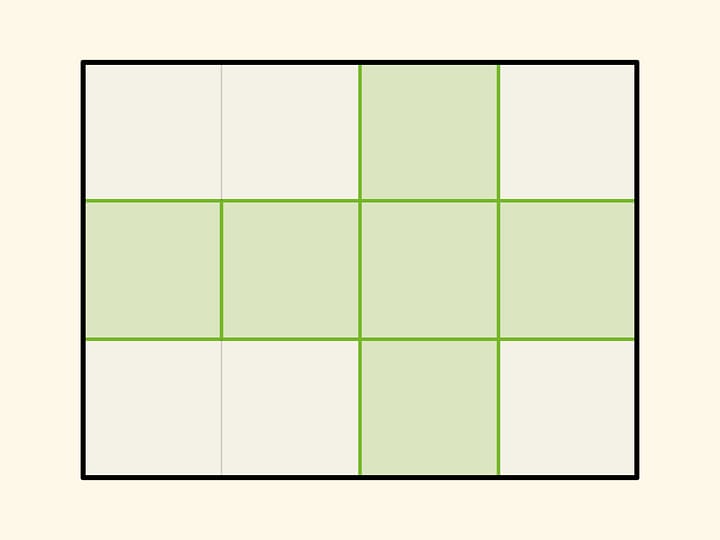
В каком месте нужно взять кирпичик, чтобы он не перевешивал ни в какую сторону? Конечно, посередине. Центр тяжести одного кирпича находится на средней линии. Значит, этот кирпич можно положить на другой, сместив относительно нижнего на половину длины, и он не упадёт.
А в каком месте нужно поднимать построенную систему? Нетрудно посчитать, что центр тяжести нашей конструкции из двух кирпичей находится на прямой, смещённой на $1/4$ длины кирпича. Действительно, центр тяжести верхнего кирпича проецируется на границу нижнего, такая же масса расположена посередине нижнего кирпича. Значит, центр тяжести системы находится ровно посередине половины кирпича, т. е. на расстоянии $1/4$ длины от края.
Трактор привозит ещё один кирпич. Как мы уже посчитали, верхние два могут быть сдвинуты относительно него на одну четверть длины.
Бабочка — существо лёгкое, погрузчику приятно поиграть с ней. Но вот она садится на кирпичи. Если она села в точку, которая проецируется на нижний кирпич, то построенная лестница не развалится. Но вот она перелетела и села чуть правее, и лестница начала разваливаться. Погрузчику приходится торопиться, чтобы поддержать построенную конструкцию и не дать упасть. Это ещё раз показывает, что сдвиги на $1/2$ и $1/4$ длины кирпичей являются максимальными, когда конструкция ещё устойчива без цемента, а только под действием силы тяжести кирпичиков.
А где находится центр тяжести системы из трёх кирпичей? Центр тяжести системы верхних двух кирпичей проецируется на самую границу нижнего. Его же центр тяжести находится посередине. Но теперь массы, приложенные к этим двум точкам, неодинаковые — справа масса двух кирпичей, а слева только одного. Значит, линия, содержащая центр тяжести системы трёх кирпичей с рассматриваемыми сдвигами, делит расстояние между половиной кирпича и краем в отношении $2:1$, считая от центра. Т. е. проходит на расстоянии $1/6$ длины кирпича от края.
Таким методом можно посчитать, что, не желая пользоваться цементом, мы можем строить лестницу, сдвигая систему из верхних n кирпичей относительно края нижнего на $1/(2n)$ длины кирпича. Так мы и будем строить, получая на каждом шаге максимальный возможный сдвиг по горизонтали.
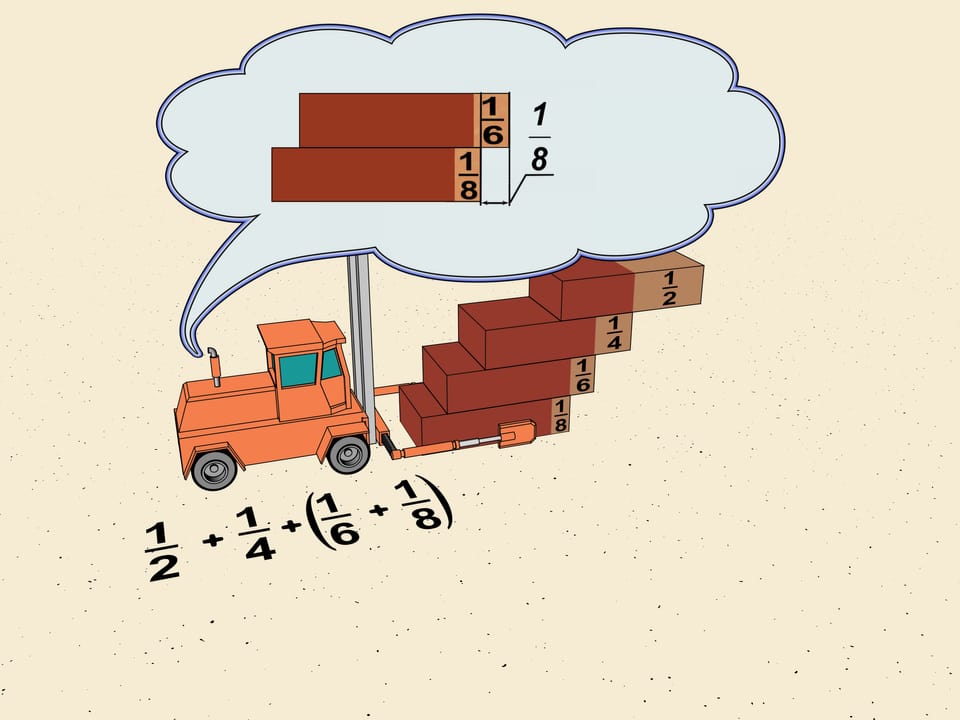
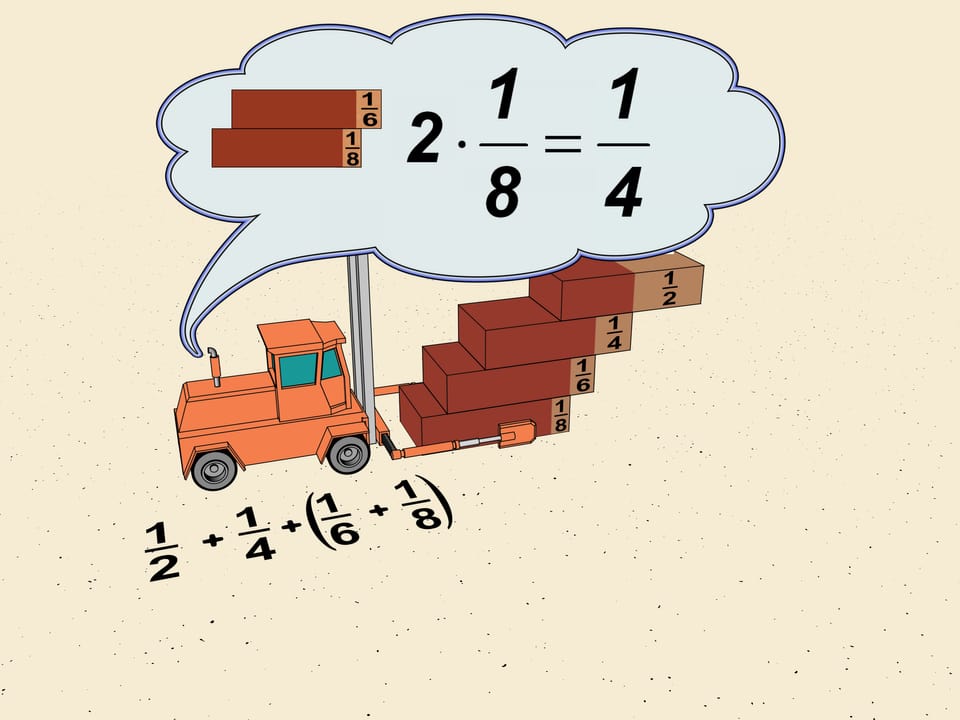
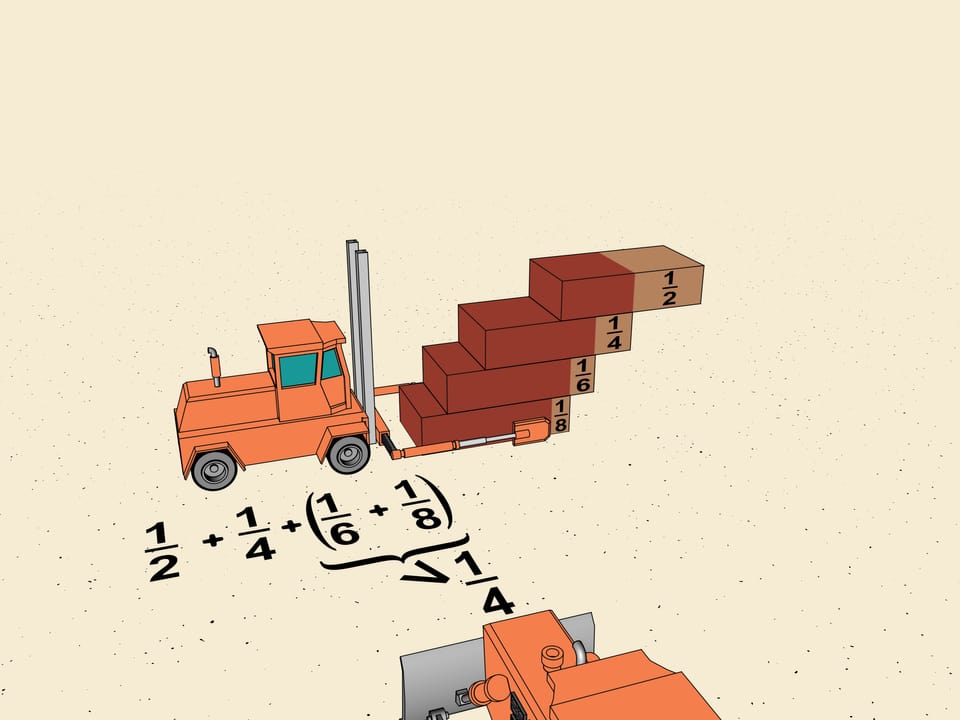
Рассмотрим первые сдвиги уже построенной лестницы. Это $1/2$, $1/4$, $1/6$, $1/8$. Не трогая первые два члена, сгруппируем $1/6$ и $1/8$, как математики говорят, в «блок». Задвинем верхний кирпичик так, чтобы все сдвиги в блоке были одинаковые и равнялись наименьшему, т. е. $1/8$. Тогда суммарный сдвиг получится $2\cdot1/8=1/4$. Таким образом, сдвиг по горизонтали, даваемый этим блоком, больше (мы же задвигали один кирпичик) $1/4$ длины кирпича.
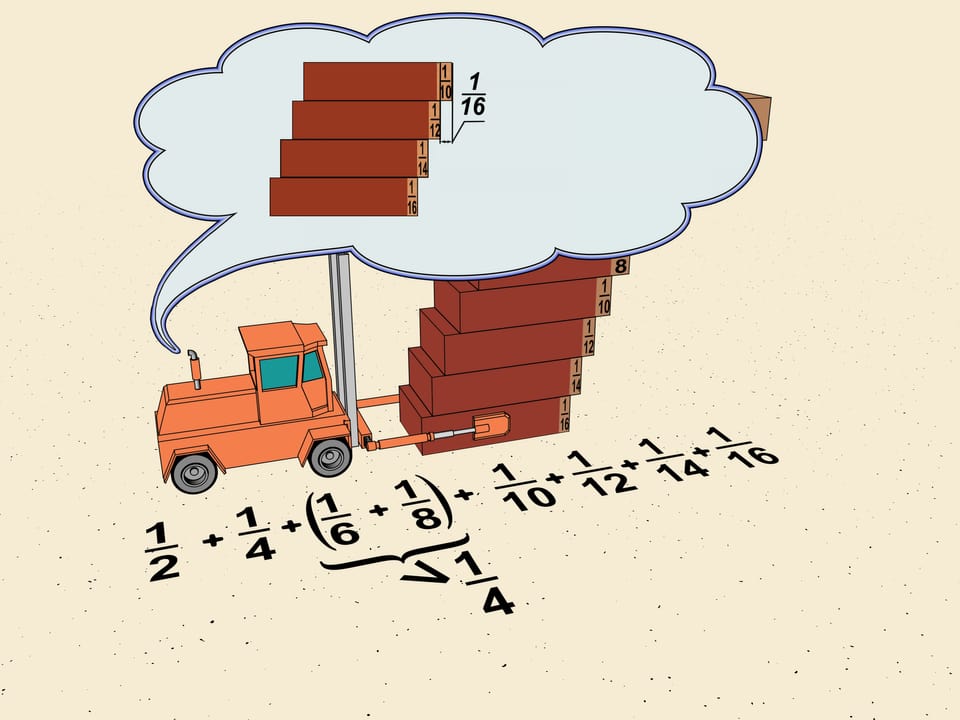
Как разбивать на блоки нашу лестницу — в нашем распоряжении. И следующий блок, который мы рассмотрим, будет состоять из четырёх кирпичиков. Это даст нам общий сдвиг на $1/10+1/12+1/14+1/16$. Чтобы оценить сдвиг в каждом блоке, будем поступать одинаково. Повторим действие, сделанное в первом блоке — задвинем верхние кирпичики так, чтобы их сдвиг равнялся наименьшему в блоке. Получим, что к горизонтальной длине лестницы четыре раза прибавляется по $1/16$, т. е. $4\cdot1/16=1/4$ длины кирпича. Значит, сдвиг по горизонтали, даваемый этим блоком, тоже больше $1/4$ длины кирпича.
Вы уже усмотрели общую схему? Следующий блок будет состоять из $2^3$ кирпичиков, и наименьший сдвиг будет на $1/2^5$ длины кирпича. Соответственно, общий сдвиг, даваемый этим блоком, будет тоже больше $1/4=2^3\cdot1/2^5$.
Таким способом можно разбить всю нашу лестницу на блоки. Блок с номером $n$ будет состоять из $2^n$ кирпичиков, и наименьший сдвиг в нём будет на $1/2^{ n+2 }$ длины кирпича. Общая длина блока будет больше чем $2^n\cdot1/2^{ n+2 }=1/4$.
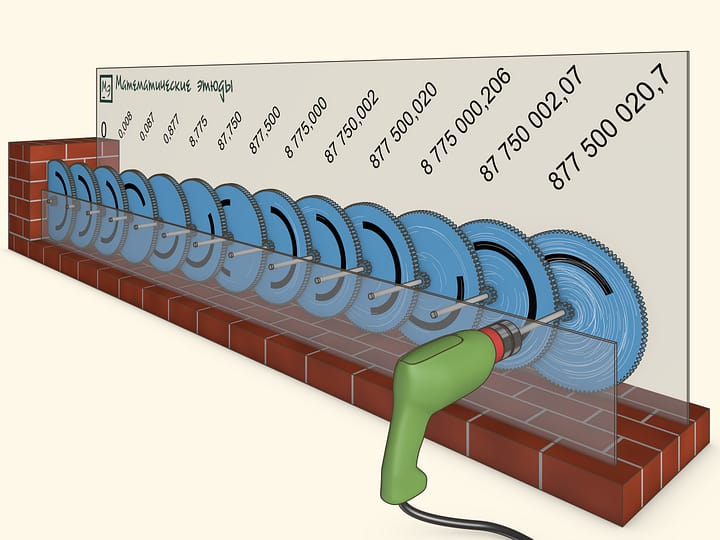
Домножим каждый член ряда на 2, а затем сократим дроби. Мы получим ряд $1+1/2+1/3+1/4+1/5+1/6+1/7+...+1/n+...$ Этот ряд называется гармоническим. Он играет большую роль в математике, и в каком-то смысле является пограничным. Если вы будете строить лестницу (уже с использованием цемента) со сдвигами большими, чем $1/n$ (т. е. в знаменателе будет стоять число меньше $n$), то такая лестница уйдёт по горизонтали в бесконечность.
В математике подобное свойство называют расходимостью ряда — какое бы ни было заранее задано большое число, всегда можно взять столько членов ряда, что их сумма будет больше заданного числа. Один из критериев расходимости — сравнение с гармоническим рядом.
Удаляясь, машинки беседуют:
— Удивительно, неужели лестница окажется и над этим местом?
— Мы же показали, что можно взять сколь угодно много блоков, каждый по длине больше $1/4$ длины кирпича…
Литература
Уфнаровский В. А. Математический аквариум. Издание 3-е, исправленное и дополненное. — М. : МЦНМО, 2014.
Paterson M., Peres Y., Thorup M., Winkler P., Zwick U. Maximum Overhang // arXiv:0707.0093.