Поместим на сферу $N$ одинаковых зарядов. К каким расположениям будут стремиться заряды, пытаясь минимизировать потенциальную энергию системы?
Данная задача возникла у Дж. Дж. Томсона при изучении планетарной модели атома. На рубеже XIX и XX веков он проводил эксперименты по нахождению наилучших расположений для небольших количеств зарядов.
Дж. Дж. Томсон 1856—1940
Джосеф Джон Томсон (J. J. Thomson) — английский физик, родился 18 декабря 1856 года. В 1884 году избран третьим Cavendish Professor. Являлся руководителем Cavendish Laboratory, Cambridge. В 1897 году экспериментально открыл существование электронов, а в 1906 году получил за это Нобелевскую премию. Умер 30 августа 1940 года. Семеро его ассистентов стали лауреатами Нобелевских премий.
После появления компьютеров проводилось множество численных экспериментов. Однако только в конце XX века некоторые частные случаи были решены математически строго.
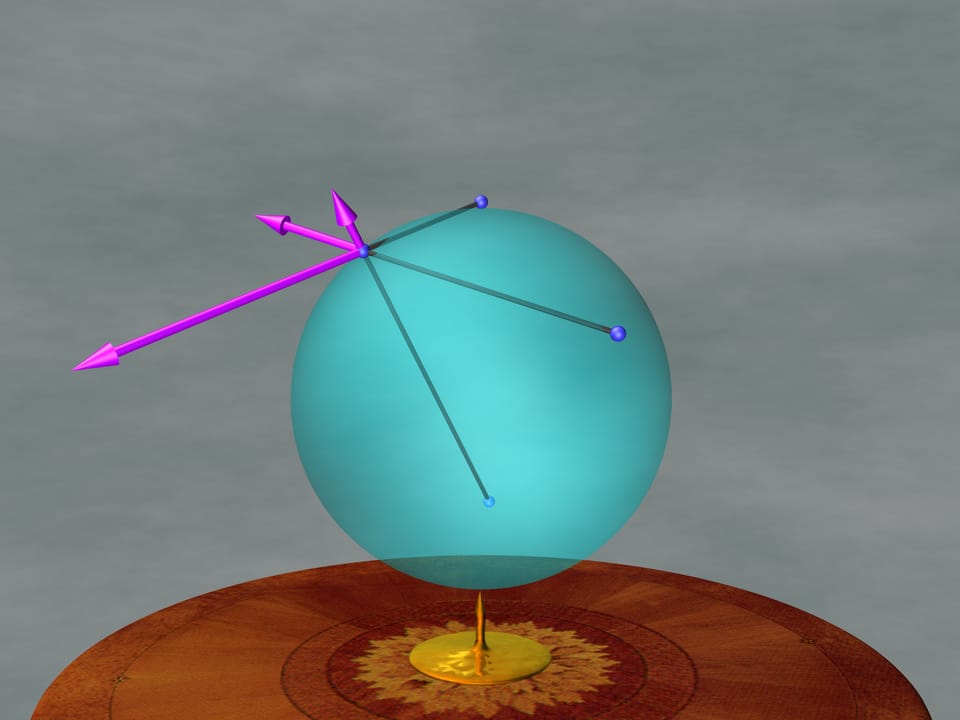
Рассмотрим, под действием каких сил двигаются электроны в задаче. Для этого зафиксируем несколько зарядов и рассмотрим силы, которые будут действовать на подвижный заряд.
Взаимодействие двух зарядов, находящихся в трёхмерном пространстве, определяется потенциалом Ньютона, обратно пропорциональным расстоянию между зарядами. Значит, чем ближе расположены заряды, тем больше сила их взаимодействия.
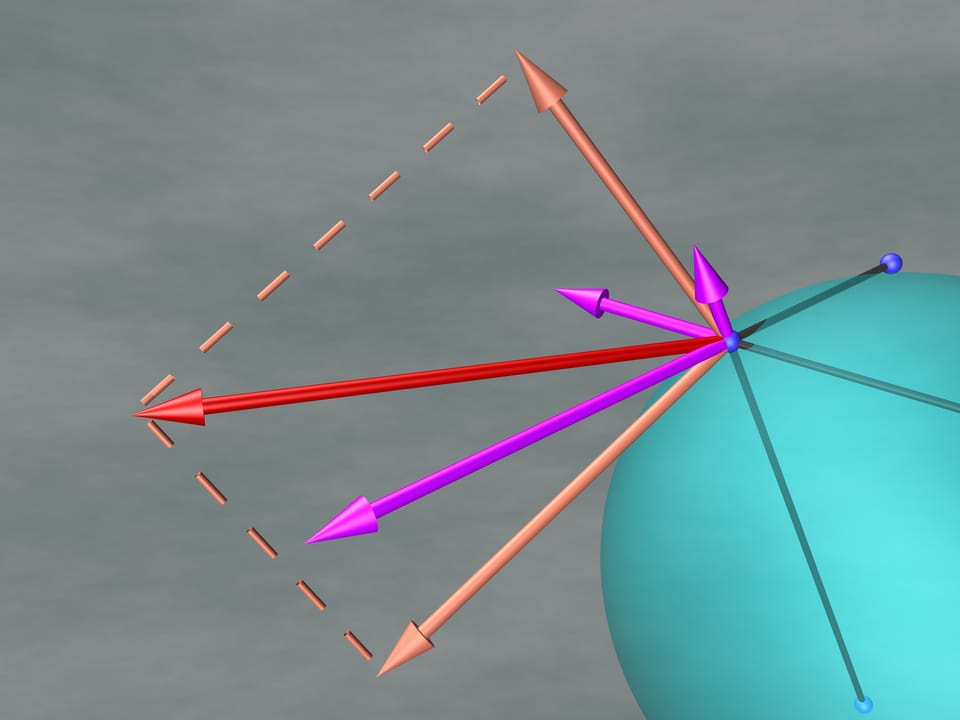
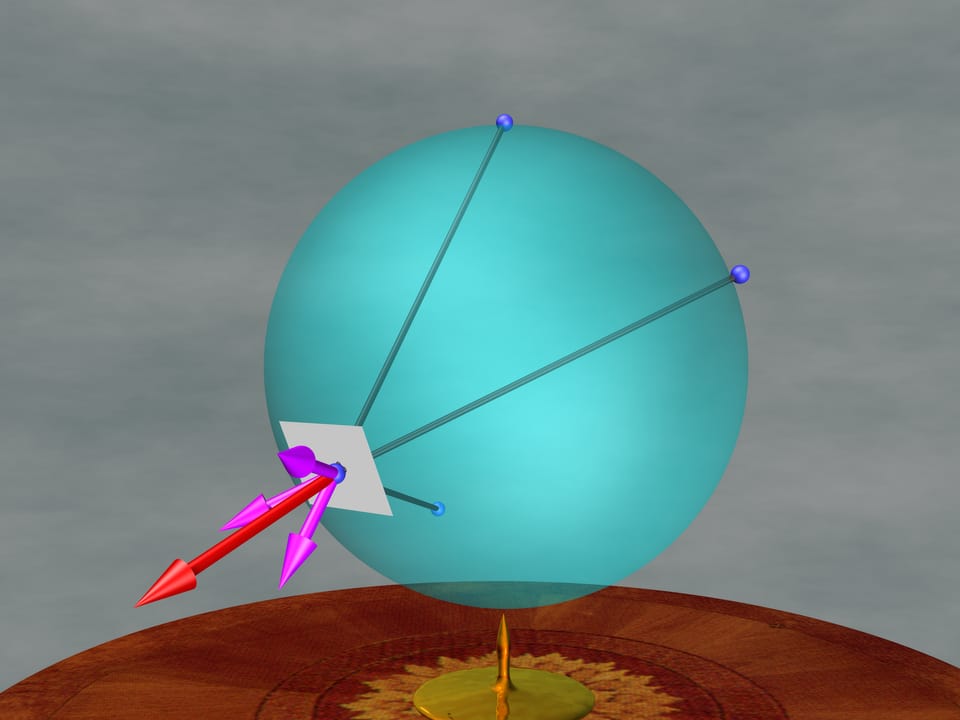
Результирующая сила равна сумме всех сил, действующих на рассматриваемый подвижный заряд. Разложим вектор силы на две составляющие: перпендикулярную к сфере и касательную. Перпендикулярная составляющая пытается вытолкнуть заряд со сферы. Значит, на движение электрона в задаче Томсона влияния она не оказывает. Касательная составляющая определяет направление и скорость движения заряда в следующий момент.
Движение свободного заряда прекратится, когда сила, действующая на него, будет перпендикулярна сфере (т. е. касательная составляющая силы будет равна нулю).
В случае системы свободных зарядов движение останавливается, когда для каждого заряда сила, действующая на него, перпендикулярна сфере.
Расположим на сфере $N$ одинаковых свободных зарядов и посмотрим, какую конфигурацию будет стремиться занять эта система.
Рассмотрим случаи, когда экстремальность полученных конфигураций удалось доказать математически строго.
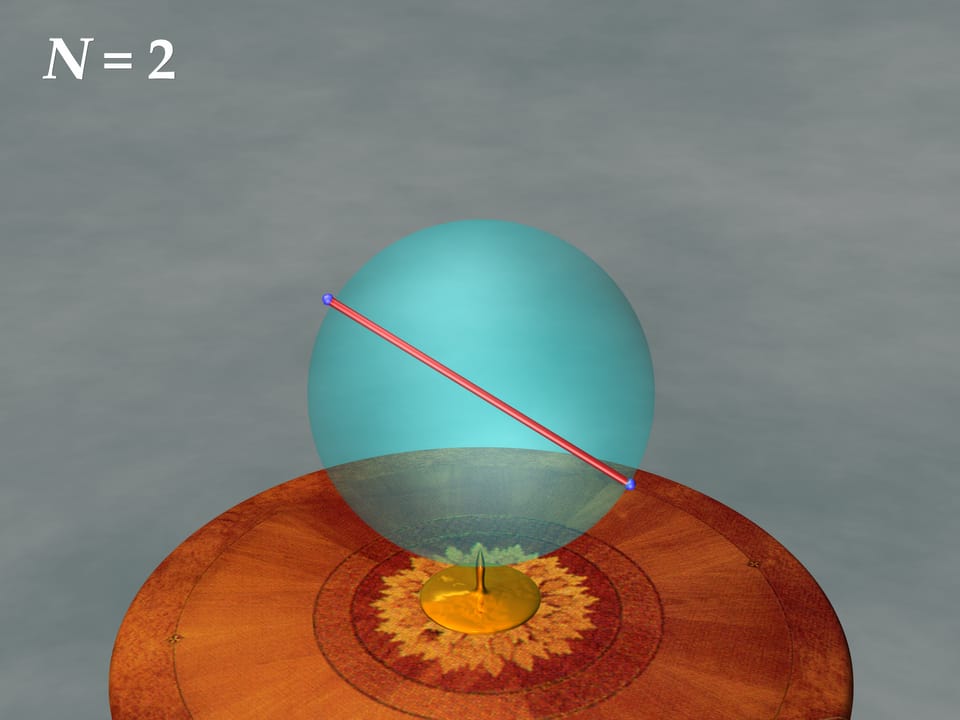
$N=2$. Два электрона расположатся в диаметрально противоположных точках.
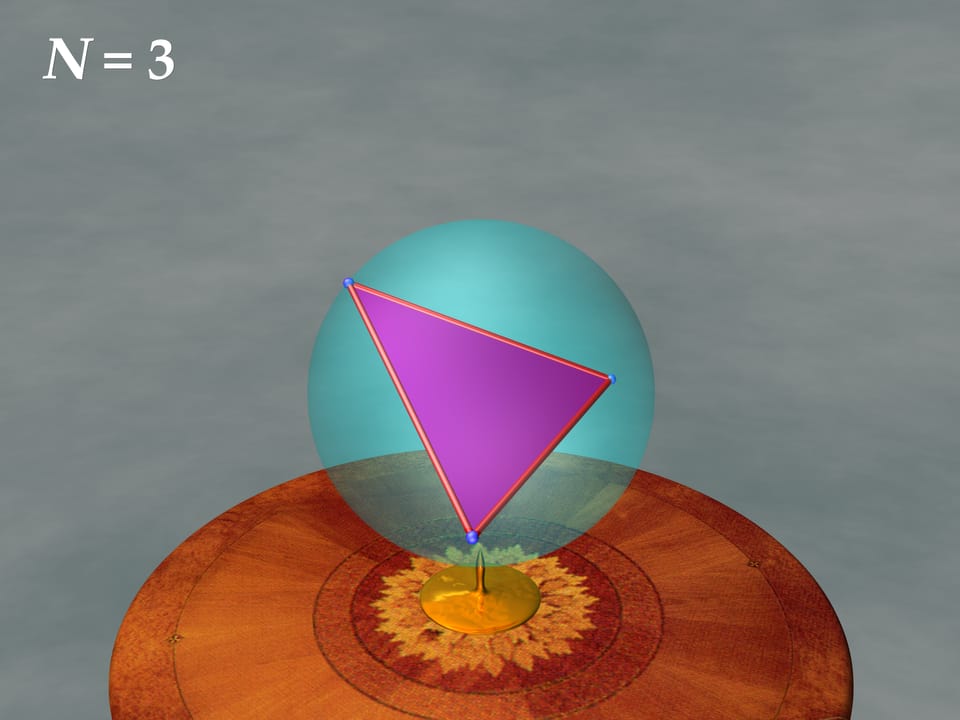
$N=3$. Через любые три точки можно провести плоскость. Плоскость пересекается со сферой по окружности. Значит, три электрона располагаются на окружности, а, следовательно, на большой окружности сферы в вершинах правильного треугольника.
$N=4$. Четыре электрона расположатся в вершинах правильного тетраэдра.
При $N=2, 3, 4$ в экстремальной конструкции все попарные расстояния между электронами одинаковы. Значит, для доказательства экстремальности приведённых конфигураций можно воспользоваться классическими неравенствами о среднем арифметическом, среднем геометрическом и среднем гармоническом. При оценке снизу потенциальной энергии системы в этих случаях перечисленные неравенства дают точные оценки, так как на экстремальных конструкциях обращаются в равенства.
$N=6$. Шесть электронов расположатся в вершинах правильного октаэдра (эту конфигурацию можно мыслить как точки пересечения осей координат трёхмерного пространства со сферой).
$N=12$. Двенадцать электронов расположатся в вершинах икосаэдра — правильного многогранника с 20 треугольными гранями и 12 вершинами.
Удивительно, но спустя век после постановки задача Томсона в трёхмерном пространстве решена только для случаев 2, 3, 4, 6 и 12 электронов на сфере. В других случаях экстремальность какой-либо конфигурации математически не доказана.
В качестве решения задачи Томсона мы встретили три из пяти правильных многогранников — тетраэдр, октаэдр и икосаэдр. А что же дают два других правильных многогранника?
$N=8$. В случае восьми электронов задача не решена. Однако легко показать, что куб не является наилучшим (в смысле минимума потенциальной энергии) расположением. Если «свернуть голову» кубу, т. е. повернуть одно основание относительно другого на $45^\circ$, получится антипризма. Внутри каждого из двух оснований энергия взаимодействия зарядов не изменяется, однако расстояние между электронами разных оснований увеличивается. Значит, антипризма лучше, чем куб, однако является ли она или какая-то другая конфигурация наилучшим расположением электронов, не доказано.
$N=20$. В случае 20 электронов, так же как и в случае восьми, можно привести расположение, которое обладает меньшей потенциальной энергией, чем додекаэдр.
Рассмотрим первый нерешённый случай — случай пяти электронов на сфере. Численные расчёты показывают, что наилучшее расположение электронов следующее: три электрона в вершинах правильного треугольника, вписанного в экватор, и два электрона по полюсам. Однако математически доказать то, что эта конструкция является наилучшей, пока не удаётся.
На примере пяти электронов рассмотрим понятие равновесной конфигурации. Задача Томсона состоит в нахождении расположения зарядов, соответствующего глобальному минимуму потенциальной энергии системы. Существуют и другие конфигурации, придя к которым система стабилизируется. Они и называются равновесными. Однако энергия таких конфигураций может быть не минимальной. Кроме того, эти конфигурации не являются устойчивыми: если пошевелить один или несколько зарядов в ней, то конфигурация распадается.
Если изначально брошенные на сферу электроны все оказались на экваторе, то никуда с экватора они не уйдут (нет сил, выталкивающих их с экватора, все силы взаимодействия лежат в плоскости экватора). Расположатся они в вершинах правильного пятиугольника.
Рассмотрим ещё одну равновесную конфигурацию. Четыре электрона в вершинах квадрата и один на перпендикулярной к этой плоскости прямой. Конфигурация так и останется четырехугольной пирамидой, подобрав наилучшую для минимума энергии высоту.
При увеличении числа зарядов количество равновесных конфигураций стремительно растёт. Это осложняет исследование задачи методами численного моделирования, даже при использовании мощных современных компьютеров.
Важные приложения имеет задача Томсона в пространствах других размерностей.
В случае двумерного пространства, т. е. плоскости, сфера — это окружность. Значит, система $N$ одинаковых зарядов находится на окружности. Пытаясь минимизировать потенциальную энергию системы, они расположатся в вершинах правильного N-угольника.
В размерностях больше трёх задача Томсона математически строго решена лишь в редких случаях.
П. Л. Чебышев 1821—1894
Пафнутий Львович Чебышев — русский математик и механик. Начал исследования по новым направлениям в разных областях: теории приближения функций, теории вероятностей, теории чисел, интегральном исчислении и т.д. Создатель известных механизмов. Являлся членом Петербургской, Берлинской и Болонской академий, Парижской Академии наук, членом-корреспондентом Лондонского Королевского общества, Шведской академии наук.
Например, доказано, что в четырёхмерном пространстве 120 электронов расположатся в вершинах правильного многогранника, имеющего соответствующее число вершин.
Некий рекорд поставлен в 24-мерном пространстве. Минимум потенциальной энергии системы из 196560 зарядов на сфере этого пространства достигается, если заряды расположены в концах минимальных векторов знаменитой решётки Лича.
Известные точные решения задачи Томсона получены методами теории приближения функций. Эта область науки, развитая российским математиком Пафнутием Львовичем Чебышевым и его учениками, является мощным методом решения разного круга задач.
Отметим, что в фильме не учитывались динамические эффекты, возникающие при движении зарядов. Такая модель возможна, если между зарядами и сферой есть сила трения.
Аккуратно, с точки зрения физики, задача Томсона может быть сформулирована так: в какие точки на сфере нужно поместить $N$ одинаковых зарядов, чтобы конфигурация соответствовала минимальной потенциальной энергии системы?
Литература
Whyte L. L. Unique arrangements of points on a sphere // The American Mathematical Monthly. — 1952. — V. 59, No. 9. — P. 606—611.
Юдин В. А. Минимум потенциальной энергии точечной системы зарядов // Дискретная математика. — 1992. — Т. 4, вып. 2. — С. 115—121.
Andreev N. N. One extremal property of the icosahedron // East Journal on Approximation. — 1996. — V. 2, No. 4. — P. 301—304.
Андреев Н. Н., Юдин В. А. Экстремальные расположения точек на сфере // Математическое просвещение (третья серия). — 1997. — Вып. 1. — С. 115—121
(В этой статье приведено научно-популярное изложение решений задачи Томсона в трёхмерном случае. Если вы хотите исследовать задачу, изучение литературы стоит начать с этой статьи.)
Точные решения частных случаев задачи в высших размерностях и других потенциалах:
Колушов А. В., Юдин В. А. О конструкции Коркина—Золотарёва // Дискретная математика. — 1994. — Т. 6, вып. 1. — С. 155—157.
Kolushov A. V., Yudin V. A. Extremal dispositions of points on a unit sphere // Analysis Mathematica. — 1997. — V. 23, No. 1.
Андреев Н. Н. Расположение точек на сфере с минимальной энергией. // Труды Математического института им. В. А. Стеклова РАН. — 1997. — Т. 219. — С. 27—31.
Андреев Н. Н. Минимальный дизайн 11-го порядка на трёхмерной сфере. // Математические заметки. — 2000. — Т. 67, № 4. — С. 489—497.