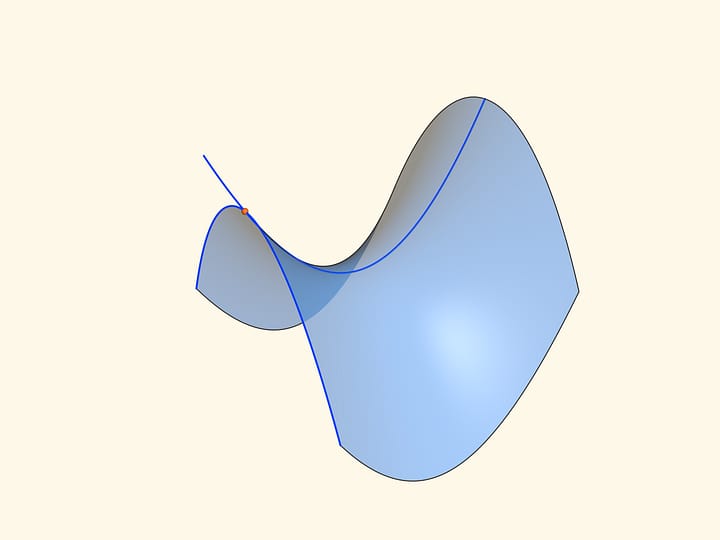
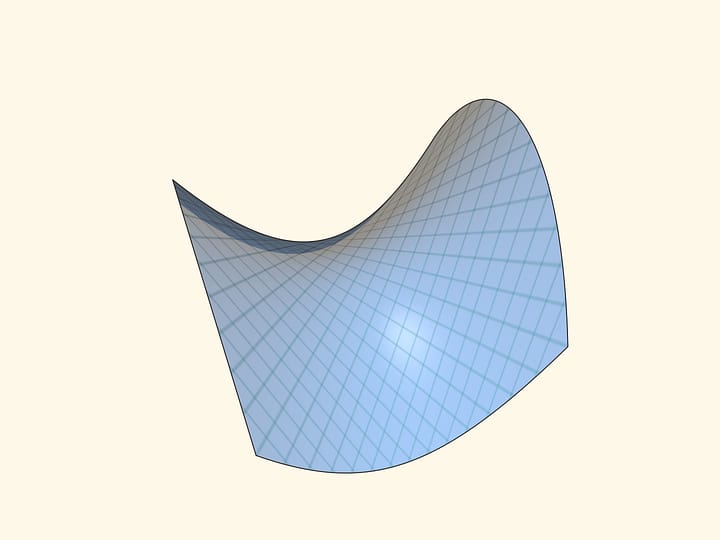
Гиперболический параболоид — поверхность, напоминающая седло. Она образуется при таком движении параболы с ветвями вниз, что её вершина скользит по другой, неподвижной параболе с ветвями вверх. Плоскости парабол в каждый момент времени перпендикулярны, оси параллельны.
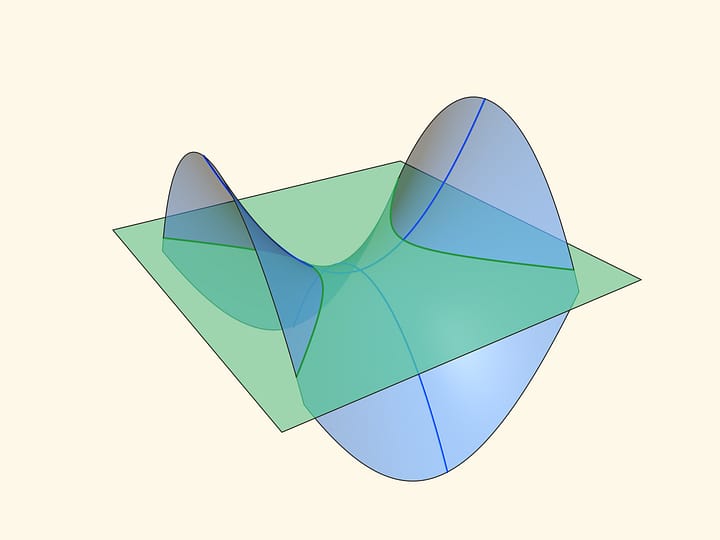
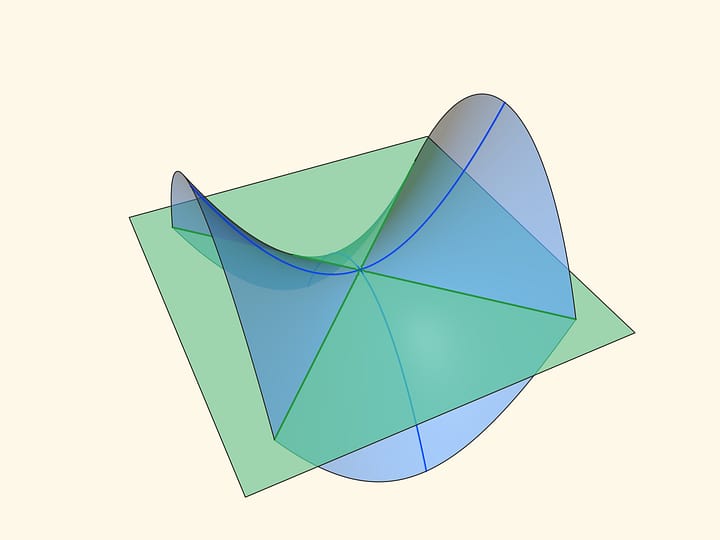
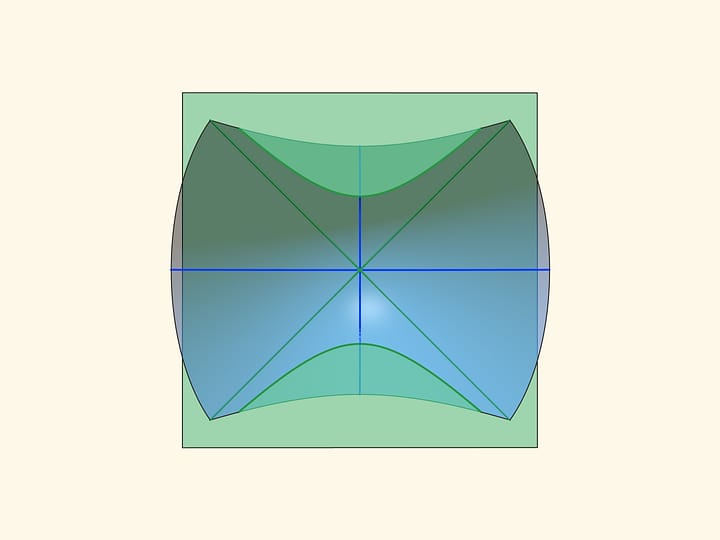
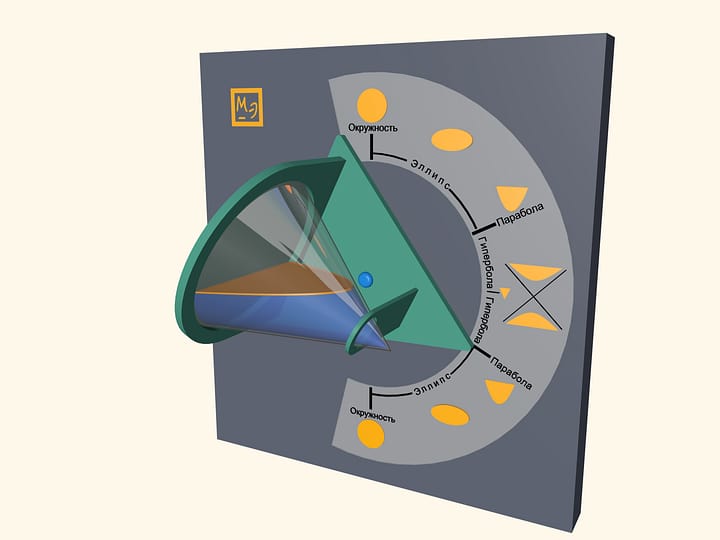
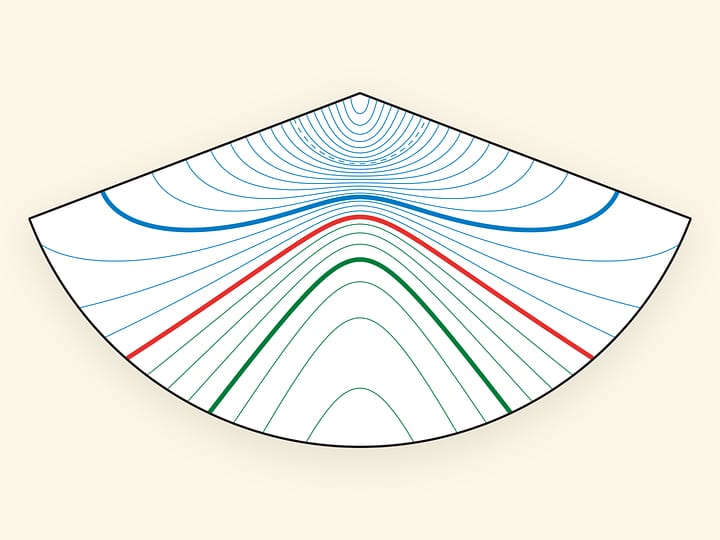
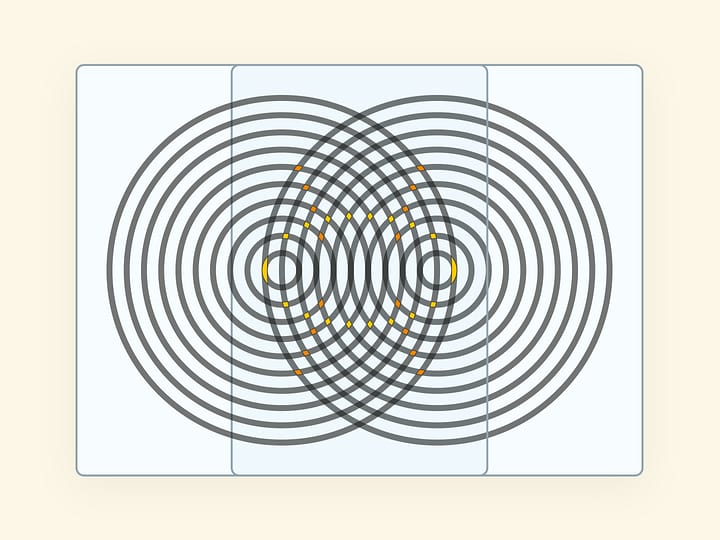
При пересечении гиперболического параболоида с любой горизонтальной плоскостью получается гипербола. Если плоскость проходит через центр седла, то гипербола вырождается в пару пересекающихся прямых. (Если на эту плоскость спроецировать гиперболу из параллельного сечения, то прямые будут асимптотами гиперболы‐проекции.)
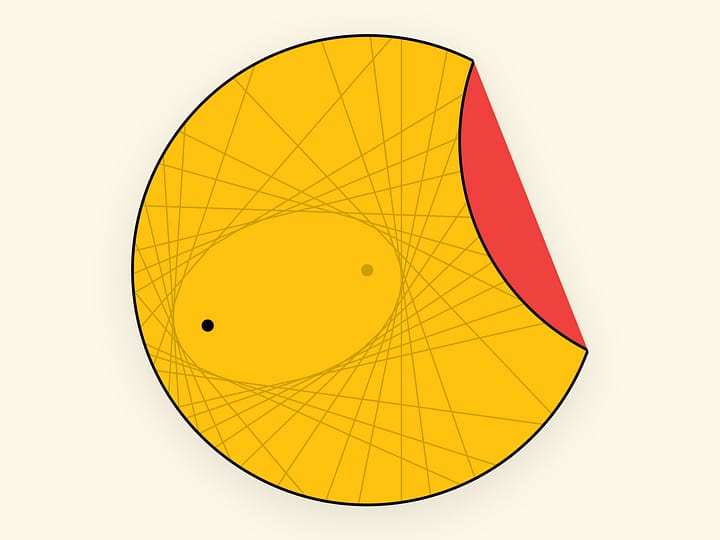
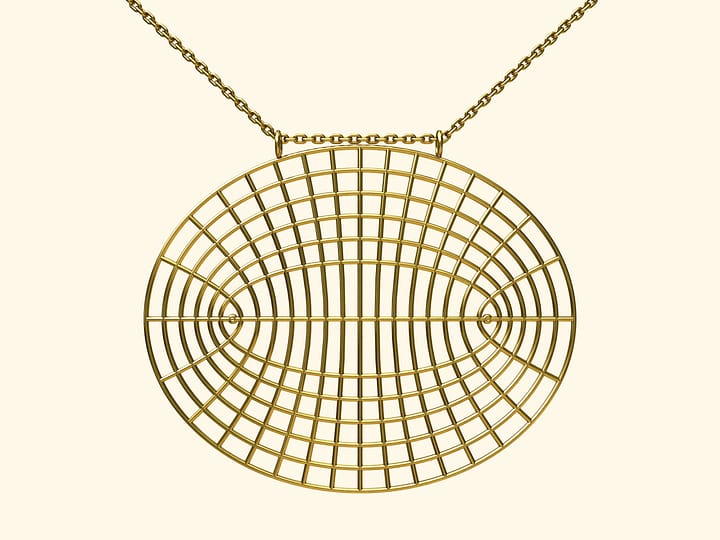
Оказывается, гиперболический параболоид — линейчатая поверхность, она также может быть образована движением прямой линии!
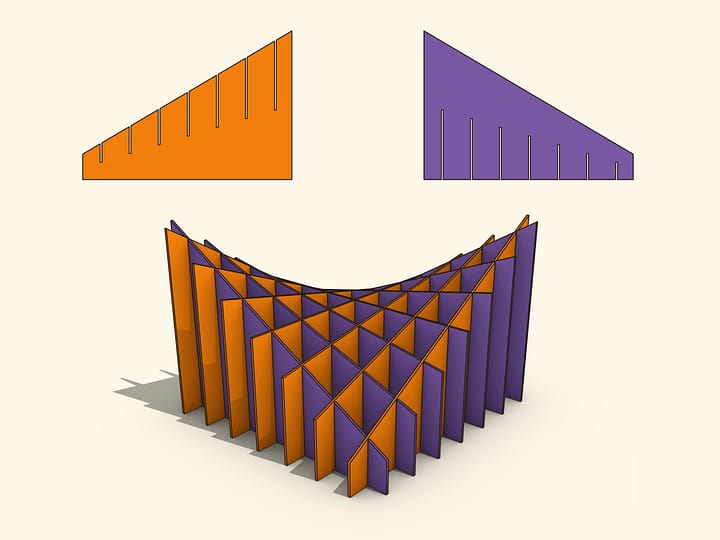
Между двумя параллельными прямыми через равные расстояния пустим набор отрезков. Повернём прямые вокруг центрального отрезка в разные стороны. (При этом длины всех отрезков, кроме центрального, изменятся.) Так расположенные в пространстве отрезки лежат на гиперболическом параболоиде.
Эта поверхность допускает красивую реализацию в виде модели из трубочек.
Гауссова кривизна во всех точках гиперболического параболоида отрицательна. Такие поверхности называют седловыми из-за визуального сходства с седлом для верховой езды.